Integrale riemann vs lebesgue
Ciao a tutti stavo cercando di capire graficamente la differenza tra i due integrali. Mi è chiara la visualizzazione delle somme superiori e inferiori di riemann che appaiono come rettangolli verticali, ma non capisco perchè nell'ottica di lebesgue vado a considerare le sezioni orizzontali.
una funzione mi è stata presentata integrabile secondo lebesgue se l'inf degli integrali delle funzione semplici maggioranti è uguale al sup degli integrali delle funzioni semplici minoranti, e l'integrale di una funzione semplice come combinazione lineare delle misure delle varie parti del dominio su cui è non nulla.
Vengono quindi usate una maggiorazione e una minorazione quindi penserei a una figura esattamente uguale a quella di riemann
grazie
una funzione mi è stata presentata integrabile secondo lebesgue se l'inf degli integrali delle funzione semplici maggioranti è uguale al sup degli integrali delle funzioni semplici minoranti, e l'integrale di una funzione semplice come combinazione lineare delle misure delle varie parti del dominio su cui è non nulla.
Vengono quindi usate una maggiorazione e una minorazione quindi penserei a una figura esattamente uguale a quella di riemann
grazie
Risposte
La mia opinione: lascia perdere. Questa distinzione non è importante. L'integrale alla fine è uno solo, non si va a distinguere tra Riemann e Lebesgue. La differenza sta da un' altra parte: nei teoremi di passaggio al limite. Quelli si che sono importanti: convergenza monotona e convergenza dominata (e lemma di Fatou e compagnia). Ragiona su quelli, non ti perdere su questi inf e sup di funzioni semplici.
si volevo solo capire l'immagine che si trova su wikipedia e mette a confronto i due metodi di integrazione
Alla pagina di wikipedia Commons relativa alla figura(*), leggo (grassetto mio):
SVG recreation of RandLintegrals.png. Compares Riemann and Lebesgue integration - I am not sure how to edit on Wikipedia, but from what I know of Lebesgue integration, this image should be changed/removed ASAP since the lower (red) drawing is false/misleading.
(*) https://commons.wikimedia.org/wiki/File ... egrals.svg
SVG recreation of RandLintegrals.png. Compares Riemann and Lebesgue integration - I am not sure how to edit on Wikipedia, but from what I know of Lebesgue integration, this image should be changed/removed ASAP since the lower (red) drawing is false/misleading.
(*) https://commons.wikimedia.org/wiki/File ... egrals.svg
Buonasera Fioravante, sempre un piacere rileggerti. In effetti quell'immagine non è mai stata una mia grande amica. Ti va di spendere due parole in più?
"Galager":
Ciao a tutti stavo cercando di capire graficamente la differenza tra i due integrali. Mi è chiara la visualizzazione delle somme superiori e inferiori di riemann che appaiono come rettangolli verticali, ma non capisco perchè nell'ottica di lebesgue vado a considerare le sezioni orizzontali.
Infatti quello che chiami "ottica di Lebesgue" è falso... E te ne sei reso conto quando hai guardato gli appunti dalle lezioni, al posto di WIKIpedia.[nota]Consiglio: lascia perdere WIKIpedia, soprattutto quella in italiano. Se proprio vuoi leggere qualcosa da lì, riferisciti sempre a quella inglese.
Anzi, detto meglio, è un teorema (che poi fornisce un modo equivalente a quello solito per introdurre l'integrale di Lebesgue, ma non posso approfondire ora...) che l'integrale di Lebesgue di una funzione nonnegativa ed integrabile sia uguale all'integrale della sua funzione di distribuzione, i.e. che:
$int_a^b f(x)\ "d" lambda = int_0^oo lambda (\{ x in [a,b]:\ f(x) > t\})\ "d" t$
(qui $lambda(*)$ è la misura di Lebesgue unidimensionale, ma l'uguaglianza vale in qualsiasi dimensione; e l'integrale al secondo membro è l'integrale di una funzione monotona e limitata, quindi lo puoi pensare anche come integrale di Riemann), ma questo vale anche per le funzioni integrabili secondo Riemann... Quindi sticazzi.
Il punto è che già dalla definizione che dai di integrale ti accorgi che le funzioni semplici che intervengono nelle stime inferiori e superiori dell'integrale di Lebesgue sono "più generali" di quelle coinvolte nell'analoga definizione dell'integrale di Riemann. Infatti, nella definizione di integrale di Riemann vai a suddividere il dominio $[a,b]$ in intervallini e, su questi, disegni funzioni semplici approssimanti per eccesso o difetto la funzione integranda; nella definizione dell'integrale di Lebesgue, invece, suddividi il codominio dell'integranda e da questa suddivisione, sfruttando la misurabilità e gli insiemi misurabili (che sono di più -ed anche molto "più brutti"- degli intervallini), ricavi le funzioni semplici approssimanti per difetto ed eccesso l'integranda.
Il secondo modo di procedere fornisce più funzioni semplici approssimanti e, detto rozzamente, ciò fa sì che ogni funzione integrabile à la Riemann sia integrabile pure à la Lebesgue (ma non viceversa) e che i due integrali coincidano.
Detto ciò, ti conviene prendere atto di una cosa: anche se molto è possibile, non tutto si può capire graficamente.
In particolare, è quasi impossibile capire graficamente in cosa l'integrale di Lebesgue differisca da quello di Riemann: infatti, siamo abituati a pensare e disegnare funzioni troppo regolari (se non proprio $C^oo$, almeno $C^oo$ a tratti e con poche discontinuità) e, per quanto detto più sopra, in questi casi gli integrali di Riemann e di Lebesgue coincidono... Quindi che differenza vuoi vedere da un grafico?
La differenza si capisce guardando la profondità e la flessibilità della teoria di Lebesgue rispetto a quella di Riemann che, come detto da dissonance, si esprimono prepotentemente nella facilità con cui è possibile passare al limite sotto il segno d'integrale.
@dissonance,
grazie per il piacere, che è reciproco
Non ho avuto tempo di rispondere, e sono contento che nel frattempo gugo82 abbia dato una risposta vista la quale non saprei cosa aggiungere che possa essere utile.
Nel mio commento volevo solo sottolineare come già su wiki commons ci fossero perplessità sulla figura. La quale figura, banalmente, difficilmente può dire qualcosa visto che la funzione di cui si occupa è troppo bella. Brevemente, direi che sarebbe stato opportuno:
- prendere una funzione più brutta
- rendere evidente che con Riemann "si tira su(*)" a partire da intervallini presi sull'asse delle $x$, mentre con Lebesgue si "tira orizzontalmente" a partire dall'asse delle $y$
Ma concordo (ovviamente) con gugo82. Se uno è arrivato a studiare l'integrale di Lebesgue, a meno che non sia successo perché ha un prof balordo, non avrebbe bisogno di questi disegnini (oh, per me i disegnini servono sempre, anche per Analisi VII, ma laddove servono)
(*) Cit. A memoria imperitura della mia prof di Geometria I
grazie per il piacere, che è reciproco
Non ho avuto tempo di rispondere, e sono contento che nel frattempo gugo82 abbia dato una risposta vista la quale non saprei cosa aggiungere che possa essere utile.
Nel mio commento volevo solo sottolineare come già su wiki commons ci fossero perplessità sulla figura. La quale figura, banalmente, difficilmente può dire qualcosa visto che la funzione di cui si occupa è troppo bella. Brevemente, direi che sarebbe stato opportuno:
- prendere una funzione più brutta
- rendere evidente che con Riemann "si tira su(*)" a partire da intervallini presi sull'asse delle $x$, mentre con Lebesgue si "tira orizzontalmente" a partire dall'asse delle $y$
Ma concordo (ovviamente) con gugo82. Se uno è arrivato a studiare l'integrale di Lebesgue, a meno che non sia successo perché ha un prof balordo, non avrebbe bisogno di questi disegnini (oh, per me i disegnini servono sempre, anche per Analisi VII, ma laddove servono)
(*) Cit. A memoria imperitura della mia prof di Geometria I
Se vuoi vedere un interpretazione geometrica di cosa vuol dire fare l'integrale di Lebesgue leggiti la prefazione di The bochner Integral, di Jan Mikusinski.
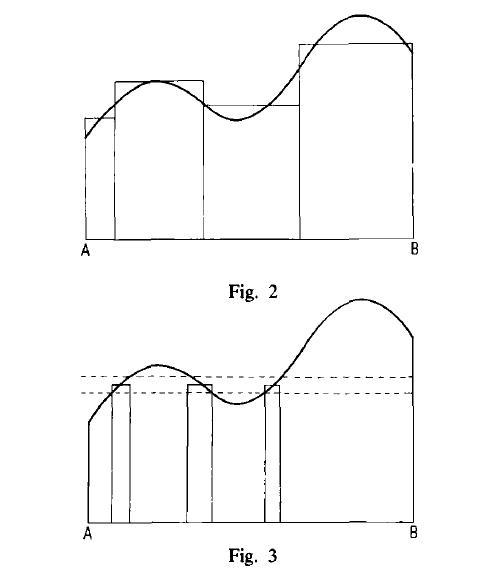
A piece of leather, like in Figure 1, is given. The task consist in measuring its area. There are three shoemakers and each of them solves the task in his own way. The shoemaker R. divides the leather into a finite number of vertical strips and considers the strips approximately as rectangles. the sum of areas of all rectangles is taken for an approximate area of the leather (Figure 2). If he is not satsified with the obtained exactitude, he repeats the whole procedure, by dividing the leather into thinner strips.
The shoemaker L. has another method. He first draws a finite number of horizontal lines. To each pair of adjacent lines he constructs a system of rectangles, as indicated in Figure 3. He finds the sum of areas of those rectangles, by multiplying their common height by the sum of lengths of their bases. He proceed in the same way with each pair of adjacent lines and sums up the obtained results. If he is not staisfied with the obtained exactitude, he repeats the whole procedure with a denser set of horizontal lines.

Chissà che metodo usa il terzo calzolaio
"Fioravante Patrone":
Chissà che metodo usa il terzo calzolaio



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo