Integrale doppio, da risolvere con una rotazione?
$int int_D (x+y)^2 / ((x+y)+1) dx dy$
$D={(x,y) \in RR^2 : |x|+|y|<=2}$
Guardando l'integranda sembra ovvio trasformare le coordinate $(x,y)$ in $(u,v)$ con $u$ o $v$ uguale a $x+y$ (nel ragionamento seguente assumo $u=x+y$), e a giudicare dalle parentesi superflue al denominatore sembra che tale sostituzione sia esplicitamente suggerita dal professore.
e come scegliere invece la coordinata $v$? guardo il dominio:
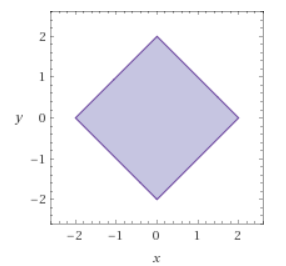
si tratta del luogo dei punti aventi distanza da $(0,0)$ minore o uguale 2 nella metrica $||\bar x||_1$, ma penso sia inutile coinvolgere il concetto di metrica.
dati i valori assoluti su x e y, potrei ragionare per singolo quadrante considerando:
primo quadrante:
$x+y<=2$
secondo quadrante:
$-x+y<=2$
terzo quadrante:
$-x-y<=2$
quarto quadrante:
$x-y<=2$
ma così facendo mi sembra di prendere una via inutilmente complicata, anche se mi sembra di vedere giustificata la trasformazione $v=x-y$ che ho visto utilizzata in esercizi simili.
come approccio alternativo vedo che si tratta di un quadrato inclinato di 45°, ma ho l'impressione che non sia necessario andare a scomodare le rotazioni dalla geometria.
assumendo la trasformazione $v=x-y$ avrei anche già calcolato la primitiva dell'integrale rispetto a $u$, ma non vedo una giustificazione per tale trasformazione.
$int u^2/(u+1) du= int (u^2-1+1)/(u+1) du = int (((u+1)(u-1))/(u+1)+1/(u+1)) du=int (u-1+1/(u+1)) du= u^2/2 -u+log(|u+1|)+c $
a intuito mi verrebbe da integrare sul quadrato $-2
$D={(x,y) \in RR^2 : |x|+|y|<=2}$
Guardando l'integranda sembra ovvio trasformare le coordinate $(x,y)$ in $(u,v)$ con $u$ o $v$ uguale a $x+y$ (nel ragionamento seguente assumo $u=x+y$), e a giudicare dalle parentesi superflue al denominatore sembra che tale sostituzione sia esplicitamente suggerita dal professore.
e come scegliere invece la coordinata $v$? guardo il dominio:

si tratta del luogo dei punti aventi distanza da $(0,0)$ minore o uguale 2 nella metrica $||\bar x||_1$, ma penso sia inutile coinvolgere il concetto di metrica.
dati i valori assoluti su x e y, potrei ragionare per singolo quadrante considerando:
primo quadrante:
$x+y<=2$
secondo quadrante:
$-x+y<=2$
terzo quadrante:
$-x-y<=2$
quarto quadrante:
$x-y<=2$
ma così facendo mi sembra di prendere una via inutilmente complicata, anche se mi sembra di vedere giustificata la trasformazione $v=x-y$ che ho visto utilizzata in esercizi simili.
come approccio alternativo vedo che si tratta di un quadrato inclinato di 45°, ma ho l'impressione che non sia necessario andare a scomodare le rotazioni dalla geometria.
assumendo la trasformazione $v=x-y$ avrei anche già calcolato la primitiva dell'integrale rispetto a $u$, ma non vedo una giustificazione per tale trasformazione.
$int u^2/(u+1) du= int (u^2-1+1)/(u+1) du = int (((u+1)(u-1))/(u+1)+1/(u+1)) du=int (u-1+1/(u+1)) du= u^2/2 -u+log(|u+1|)+c $
a intuito mi verrebbe da integrare sul quadrato $-2
Risposte
La rotazione di 45° non è "da scomodare dalla geometria", è la più semplice possibile ed è data da
\[
\begin{cases}
u=\frac{1}{\sqrt 2} (x-y), \\
v=\frac{1}{\sqrt 2}(x+y),
\end{cases}
\]
mi sembra la più appropriata a questo problema. Con questa vedi subito che Wolfram Alpha torto torto non ce l'ha...
Ma forse hai dimenticato un quadrato al denominatore.
\[
\begin{cases}
u=\frac{1}{\sqrt 2} (x-y), \\
v=\frac{1}{\sqrt 2}(x+y),
\end{cases}
\]
mi sembra la più appropriata a questo problema. Con questa vedi subito che Wolfram Alpha torto torto non ce l'ha...
Ma forse hai dimenticato un quadrato al denominatore.
"dissonance":
La rotazione di 45° non è "da scomodare dalla geometria", è la più semplice possibile ed è data da
\[
\begin{cases}
u=\frac{1}{\sqrt 2} (x-y), \\
v=\frac{1}{\sqrt 2}(x+y),
\end{cases}
\]
mi sembra la più appropriata a questo problema. Con questa vedi subito che Wolfram Alpha torto torto non ce l'ha...
grazie, dimenticavo quanto fosse semplice questa trasformazione, applicandola ho ottenuto:
$int_{-sqrt(2)}^{sqrt(2)} int_{-sqrt(2)}^{sqrt(2)} (v sqrt(2))^2/(sqrt(2) v +1) dv du $
e l'integrale non converge in quanto l'integranda non è limitata nel punto del dominio con la coordinata $v=-1/sqrt(2)$
Ma forse hai dimenticato un quadrato al denominatore.
dove mancherebbe un quadrato?
dico, forse il denominatore era \((x+y)^2+1\)
"dissonance":
dico, forse il denominatore era \((x+y)^2+1\)
il testo è proprio così


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo