Dominio di una trasformazione
Scusate la domanda forse banale ma non riesco a capire questo passaggio.
Ho due variabili $x,y=\mathbb(1)_{(0,1)}(\cdot)$ e un integrale doppio $\int_(0)^(1)\int_(0)^(1)g(xy)dxdy$, con $g$ funzione qualsiasi.
Applico la trasformazione $\tau:={ ( x=u ),( v=xy ):}$ con $dxdy:=1/u dudv$. Bene.
Perchè a seguito di ciò il dominio di $u$ resta (ovviamente) $0
Credo che riuscendo a capire questo, probabilmente verrei a capo del passaggio successivo:
Ho due variabili $x,y=\mathbb(1)_{(0,1)}(\cdot)$ e un integrale doppio $\int_(0)^(1)\int_(0)^(1)g(xy)dxdy$, con $g$ funzione qualsiasi.
Applico la trasformazione $\tau:={ ( x=u ),( v=xy ):}$ con $dxdy:=1/u dudv$. Bene.
Perchè a seguito di ciò il dominio di $u$ resta (ovviamente) $0
Credo che riuscendo a capire questo, probabilmente verrei a capo del passaggio successivo:
Risposte
gira e rigira sempre lì si arriva
${{: ( U=X ),( V=XY ) :} rarr{{: ( X=U ),( Y=V/U) :}$
da cui è evidente che, ricordando che stavolta $V in (0;1)$
$0V rarr 0
e quindi....
$int_(v)^1 1/u du=-logv mathbb{1}_((0;1))(v)$
che è la tua densità cercata....
next step: $V=X/Y$
ma i casi sono migliaia....l'unico modo per risolvere il problema è studiare gli integrali doppi....
[ot]ho tagliato corto perché so dove l'utente vuole arrivare (o almeno penso di saperlo)....[/ot]
${{: ( U=X ),( V=XY ) :} rarr{{: ( X=U ),( Y=V/U) :}$
da cui è evidente che, ricordando che stavolta $V in (0;1)$
$0
e quindi....
$int_(v)^1 1/u du=-logv mathbb{1}_((0;1))(v)$
che è la tua densità cercata....
next step: $V=X/Y$
ma i casi sono migliaia....l'unico modo per risolvere il problema è studiare gli integrali doppi....
[ot]ho tagliato corto perché so dove l'utente vuole arrivare (o almeno penso di saperlo)....[/ot]
Ho capito, mi sono munito di Pagani-Salsa e per il momento mi concentro solo sulla doppia integrazione. Poi mi studierò per bene la tua risposta.
Tanto ho capito che se non ho ben chiaro questo è inutile andare avanti.
Grazie tommik
Tanto ho capito che se non ho ben chiaro questo è inutile andare avanti.
Grazie tommik
Ho dato uno sguardo alla doppia integrazione sul Pagani-Salsa (Cambiamento delle variabili di integrazione, 1.6, pag. 311-321). Ottimo libro per laureandi in matematica se si ha bisogno di giustificare passaggi ed oltre mediante lemmi e dimostrazioni, ma non è quello che serve a me. Sto cercando dei libri con esercizi (meglio se svolti) che trattino di integrazione multipla per capire, in particolare, come cavolo si applica 'sto cambiamento di variabili se si operano trasformazioni. Sul Pagani ci sono 2 esempi per puzza: uno di una funzione in due variabili in $x^2+y^2$ che si trasforma tramite coordinate polari, e un altro di una funzione in due variabili in $x+y$ che la somma stessa e la sua inversa. Avete qualche titolo da consigliarmi?
"mobley":
Ho dato uno sguardo alla doppia integrazione sul Pagani-Salsa (Cambiamento delle variabili di integrazione, 1.6, pag. 311-321). Ottimo libro […]
E basta.
Non c’è bisogno di aggiungere altro.
"mobley":
[…] se si ha bisogno di giustificare passaggi ed oltre mediante lemmi e dimostrazioni
Che è ciò che si fa qualunque volta si faccia della Matematica.
Dopotutto, anche le operazioni “in colonna” servono a giustificare i risultati, cioè a dimostrare.
"mobley":
non è quello che serve a me. Sto cercando dei libri con esercizi (meglio se svolti) che trattino di integrazione multipla per capire, in particolare, come cavolo si applica 'sto cambiamento di variabili se si operano trasformazioni. […] Avete qualche titolo da consigliarmi?
Dopo aver studiato la teoria, prenditi un eserciziario adatto al tuo livello. Marcellini & Sbordone, ad esempio.
Poi, non si capisce cosa vuoi.
Speri di capire qualcosa di Probabilità senza avere basi decenti di Analisi?
"gugo82":
Dopo aver studiato la teoria, prenditi un eserciziario adatto al tuo livello. Marcellini & Sbordone, ad esempio.
Ti ringrazio. Ora do un occhiata. In ogni caso la teoria sul merito sul Pagani-Salsa sono due pagine e mezzo (e non è un eufemismo), il che mi rincuora e non poco.
"gugo82":
Poi, non si capisce cosa vuoi.
Voglio capire il motivo per cui, partendo dalle informazioni di cui al post di apertura, il docente dice che:

"gugo82":
Speri di capire qualcosa di Probabilità senza avere basi decenti di Analisi?
Non spero. Devo.
"mobley":
[quote="gugo82"]Dopo aver studiato la teoria, prenditi un eserciziario adatto al tuo livello. Marcellini & Sbordone, ad esempio.
Ti ringrazio. Ora do un occhiata. In ogni caso la teoria sul merito sul Pagani-Salsa sono due pagine e mezzo (e non è un eufemismo), il che mi rincuora e non poco.[/quote]
Evidentemente usa ipotesi sufficientemente buone da dimostrare la cosa in poche parole… In generale, il cambiamento di variabili negli integrali multipli è un teorema difficile.
"mobley":
[quote="gugo82"]Poi, non si capisce cosa vuoi.
Voglio capire il motivo per cui, partendo dalle informazioni di cui al post di apertura, il docente dice che:
 [/quote]
[/quote]Te l'ha già spiegato, in termini più che comprensibili, tommik.
"mobley":
[quote="gugo82"]Speri di capire qualcosa di Probabilità senza avere basi decenti di Analisi?
Non spero. Devo.[/quote]
Prescrizione medica?
"gugo82":
Te l'ha già spiegato, in termini più che comprensibili, tommik.
@mobley: tanto per concludere ti mostro anche ciò che il docente ti farà vedere domani, sempre trasformando il solito vettore di uniformi indipendenti su $(0;1)$ (almeno ti porti avanti con la spiegazione che, per ovvi motivi, potrebbe anche seguire una strada diversa pur raggiungendo il medesimo risultato)
${{: ( u=x ),( v=x/y ) :}rarr{{: ( x=u ),( y=u/v) :}rarr{{: ( 0
Ora però abbiamo che $v in (0;+oo)$ e quindi avremo 2 casi:
1) quando $0
$f_V(v)=int_0^v f(u,v)du=1/2$
2) quando $v>1$
$f_V(v)=int_0^1 f(u,v)du=1/(2v^2)$
ecco la densità di V (click per ingrandire)
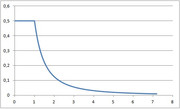
Per completare il quadro, ecco anche la rappresentazione grafica dei due dominii congiunti: uno relativo all'esempio che hai fatto tu e l'altro a quello che ho aggiunto io
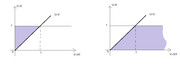
Ora facciamo un'altra strada:
^^^^^^^^^^^^^
Esempio 1), quello che hai postato tu: $f(u,v)=1/u$ nel dominio del grafico di sinistra
$f_U(u)=int_0^u 1/udv=1$
(integro in orizzontale e, come ci si aspettava, si trova la densità di una uniforme su $(0;1)$)
$f_V(v)=int_v^1 1/u du=-logv$,
(integro in verticale e, come ottenuta per altra strada, trovo la marginale V)
^^^^^^^^^^^^^^^^^^
^^^^^^^^^^^^^^^
Esempio 2): quello che ho aggiunto io dove $V=X/Y$ e dove il dominio è quello disegnato nel grafico di destra
$f_U(u)=int_u^(+oo) u/v^2 dv=1$ (integro in orizzontale e, come ci si aspettava, ecco la densità uniforme)
$f_V(v)=...$ integrando in verticale otterrai la densità che ho trovato prima per altra strada.
Tutti questi "giochetti" diventano banali dopo che si è preso dimestichezza con l'integrazione doppia, dato che ti obbliga a prendere confidenza con la definzione di un dominio doppio e le tecniche base per integrarci sopra....occhio che in probabilità avrai anche esercizi con l'integrazione tripla, che si può fare dopo che si ha dimestichezza con quella doppia....
Tutto ciò, non per risolverti un esercizio, ma per farti capire che senza un adeguato studio della matematica di base non puoi andare oltre.... IMHO
Eh tommik, è da stamattina che sto sbattendo la testa su sti domini maledetti, grafici ma sbaglio sempre a definire gli estremi



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo