Dominio di F(x)
ciao ragazzi,
come studiereste il dominio ed il segno di questa funzione?
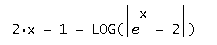
come studiereste il dominio ed il segno di questa funzione?
Risposte
l'unica cosa che potrebbe creare qualche problema è il logaritmo, ma l'argomento è in modulo, quindi devo escludere solo i valori per cui è uguale a 0.
e^x-2=0 e^x=2
x=ln2
WonderP.
e^x-2=0 e^x=2
x=ln2
WonderP.
si il dominio è quello, ma per il segno ?
E' da studiare graficamente. Disegni separatamente 2x-1 (retta) e la funzione logaritmo che hai.
Luca.
Luca.
cioè mi studio a parte le due funzioni ?
g(x) = 2x - 1; e t(x) = log( |e^x - 2| )
e poi vedo se g(x) è più grande di t(x) ? ed in questo caso cosa vorrebbe dire ? che se :
1. gx > tx allora la funzione è sempre positiva
2. se gx < tx allora la fx è sempre negativa
? dico bene ?
g(x) = 2x - 1; e t(x) = log( |e^x - 2| )
e poi vedo se g(x) è più grande di t(x) ? ed in questo caso cosa vorrebbe dire ? che se :
1. gx > tx allora la funzione è sempre positiva
2. se gx < tx allora la fx è sempre negativa
? dico bene ?
Esatto, potresti anche trovare una o piu' intersezioni; allora quelle sono zeri per la funzione data e al passare delle intersezioni hai un cambio di segno.
Luca.
Luca.
Scusa, non mi ero accorto che chiedevi anche il segno. Va beh, grazie Luca.
WonderP.
WonderP.
quote:
Originally posted by Luca77
Esatto, potresti anche trovare una o piu' intersezioni; allora quelle sono zeri per la funzione data e al passare delle intersezioni hai un cambio di segno.
Luca.
me la spieghi meglio questa cosa Luca ? se ti va...
Certo; se trovi intersezione tra i grafici di due funzioni f e g, allora tale punto e' uno zero per f-g. E tale punto potrebbe separare, localmente, una zona in cui f>g da una zona in cui f
Luca.
Luca.
ah si ho capito allora, cioè avrebbe a che fare con il teorema degli zeri o sbaglio ?
Si, per dimostrare correttamente tutto, lo strumento e' il Teorema degli zeri per funzioni continue.
Luca.
Luca.
ok, grazie Luca 



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo