Curvatura in funzione di sviluppo.
Innanzitutto grazie dell'ospitalità in questo forum.
E' qualche tempo che sto studiando un sistema di rappresentazione di funzioni piane che tenga conto del verso di tracciamento di una curva. Il metodo che alla fine ho scelto è quello di calcolare la curvatura (ovvero 1/R = reciproco del raggio del cerchio osculatore) in ogni punto, in funzione della lunghezza dello sviluppo della curva stessa.
Le equazioni quindi sono del tipo c=F(s): curvatura=funzione di sviluppo.
Per convenzione parto da un punto e procedo verso sinistra ruotando in senso antiorario se la curvatura è positiva, orario se negativa.
la funzione c=0 è quindi una retta,
c=1 un cerchio di raggio 1,
c=2 un cerchio di raggio 0,5,
c=s una spirale antioraria che procede infinitamente verso l'interno.
La formula di una lemniscata tracciata in verticale risulta essere c=cos(s /2,40482557 ) (allego animazione del disegno:
). Trattasi di una lemniscata la cui curvatura massima è uguale ad 1.
Inizialmente pensavo essere quella di Bernoulli perché è visivamente simile ma provando a sovrapporle, la mia è più "panciuta" e l'angolo al centro risulta di 95° 29' invece dei classici 90° della lemniscata Bernoulliana.
La costante 2,40482557 l'ho trovata per tentativi cercando quel valore che mi facesse chiudere graficamente la lemniscata su se stessa. Ho cercato per un po' di riferirlo alla costante di Gauss, ma quando ho capito che la lemniscata non era quella di Bernoulli ho dovuto ricominciare da capo.
Qualcuno potrebbe aiutarmi a trovare a cosa corrisponde questo numero?
Un paragone fra la "mia" lemniscata e quella di Bernoulli si può trovare qui (ho utilizzato il seno invece del coseno perché disegna entrambe le lemniscate inclinate di 45°) :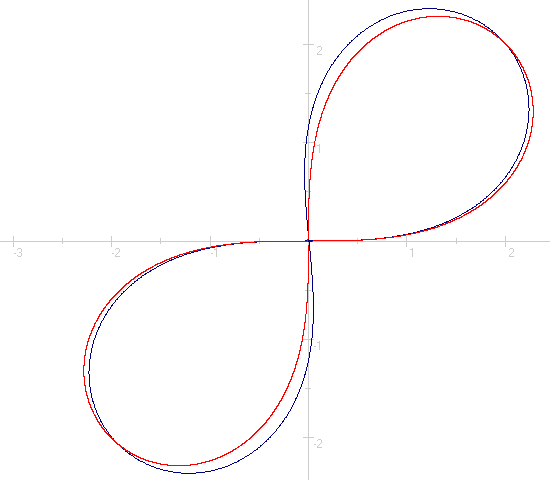
(*) ho modificato questo post perché la costante era erroneamente raddoppiata. Adesso comunque ho trovato che si tratta del primo dei valori in X che azzerano la funzione di Bessel. L'animazione non è stata modificata e visualizza il doppio del valore di S
E' qualche tempo che sto studiando un sistema di rappresentazione di funzioni piane che tenga conto del verso di tracciamento di una curva. Il metodo che alla fine ho scelto è quello di calcolare la curvatura (ovvero 1/R = reciproco del raggio del cerchio osculatore) in ogni punto, in funzione della lunghezza dello sviluppo della curva stessa.
Le equazioni quindi sono del tipo c=F(s): curvatura=funzione di sviluppo.
Per convenzione parto da un punto e procedo verso sinistra ruotando in senso antiorario se la curvatura è positiva, orario se negativa.
la funzione c=0 è quindi una retta,
c=1 un cerchio di raggio 1,
c=2 un cerchio di raggio 0,5,
c=s una spirale antioraria che procede infinitamente verso l'interno.
La formula di una lemniscata tracciata in verticale risulta essere c=cos(s /2,40482557 ) (allego animazione del disegno:
). Trattasi di una lemniscata la cui curvatura massima è uguale ad 1. Inizialmente pensavo essere quella di Bernoulli perché è visivamente simile ma provando a sovrapporle, la mia è più "panciuta" e l'angolo al centro risulta di 95° 29' invece dei classici 90° della lemniscata Bernoulliana.
La costante 2,40482557 l'ho trovata per tentativi cercando quel valore che mi facesse chiudere graficamente la lemniscata su se stessa. Ho cercato per un po' di riferirlo alla costante di Gauss, ma quando ho capito che la lemniscata non era quella di Bernoulli ho dovuto ricominciare da capo.
Qualcuno potrebbe aiutarmi a trovare a cosa corrisponde questo numero?
Un paragone fra la "mia" lemniscata e quella di Bernoulli si può trovare qui (ho utilizzato il seno invece del coseno perché disegna entrambe le lemniscate inclinate di 45°) :
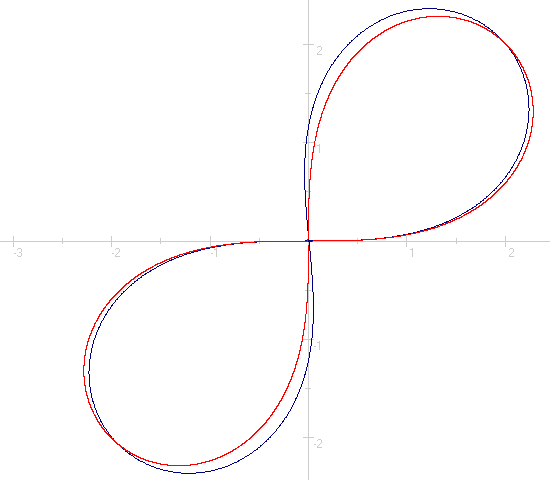
(*) ho modificato questo post perché la costante era erroneamente raddoppiata. Adesso comunque ho trovato che si tratta del primo dei valori in X che azzerano la funzione di Bessel. L'animazione non è stata modificata e visualizza il doppio del valore di S
Risposte
Chiedo scusa per il fatto che normalmente la curvatura si indica con K, mentre io ho indicato con c la curvatura e con k quel misterioso coefficiente. Disegnando le funzioni in questo modo si ottengono delle curve bellissime. Se qualcuno è interessato posso postare dei grafici.
Provando ad eguagliare la formula della curvatura di una funzione con il seno di quella dello sviluppo, sia lavorando in coordinate cartesiane che in quelle polari, otteniamo un'equazione differenziale di terzo ordine piuttosto complicata da risolvere. Questa è quella in coordinate polari che dovrebbero facilitare la rappresentazione della lemniscata:
$ (a^2 + ρ^2)^3·(3·a·b - ρ·(c - 2))/((a^2 + ρ^2)^(3/2) - 2·a^2 + ρ·(b - ρ)) - 3·a·(b + ρ)/(a^2 + ρ^2)^2 = t·√(a^2 + ρ^2) $
dove a b e c sono rispettivamente la derivata prima seconda e terza di ρ = f(Θ) e t è il reciproco della costante che sto cercando.
c è esplicitabile ma già fare a mano l'integrale della formula che segue, per ridurre di un ordine l'equazione, non è una passeggiata:
$ (√(a^2 + ρ^2)·(2·a^6 + a^4·ρ·(5·ρ - b) - 3·a^3·(b + ρ) + 2·a^2·ρ^3·(2·ρ - b) - 3·a·ρ^2·(b + ρ) - ρ^5·(b - ρ)) + 3·a^11·b + 2·a^10·ρ + 15·a^9·b·ρ^2 + a^8·(10·ρ^3 - 1) + 30·a^7·b·ρ^4 + 4·a^6·ρ^2·(5·ρ^3 - 1) + 30·a^5·b·ρ^6 + 2·a^4·ρ^4·(10·ρ^3 - 3) + 3·a^3·(b·(5·ρ^8 + 2) + 2·ρ) + 2·a^2·ρ^6·(5·ρ^3 - 2) - 3·a·ρ·(b^2 - b·ρ^9 - ρ^2) + ρ^8·(2·ρ^3 - 1))/(ρ·(a^2 + ρ^2)^5) $
Qualcuno conosce un software che possa risolvere una cosa del genere ?
A chi potrà aiutarmi farò inviare un volume a scelta dell'Opera di Corrado Brogi (mio padre) che ho recentemente pubblicato su Amazon. Purtroppo io non sono un matematico ma un informatico, il motivo per cui mi interesso di questo genere di equazioni è perché hanno una corrispondenza con i flussi di quelle che si chiamano "energie sottili".
$ (a^2 + ρ^2)^3·(3·a·b - ρ·(c - 2))/((a^2 + ρ^2)^(3/2) - 2·a^2 + ρ·(b - ρ)) - 3·a·(b + ρ)/(a^2 + ρ^2)^2 = t·√(a^2 + ρ^2) $
dove a b e c sono rispettivamente la derivata prima seconda e terza di ρ = f(Θ) e t è il reciproco della costante che sto cercando.
c è esplicitabile ma già fare a mano l'integrale della formula che segue, per ridurre di un ordine l'equazione, non è una passeggiata:
$ (√(a^2 + ρ^2)·(2·a^6 + a^4·ρ·(5·ρ - b) - 3·a^3·(b + ρ) + 2·a^2·ρ^3·(2·ρ - b) - 3·a·ρ^2·(b + ρ) - ρ^5·(b - ρ)) + 3·a^11·b + 2·a^10·ρ + 15·a^9·b·ρ^2 + a^8·(10·ρ^3 - 1) + 30·a^7·b·ρ^4 + 4·a^6·ρ^2·(5·ρ^3 - 1) + 30·a^5·b·ρ^6 + 2·a^4·ρ^4·(10·ρ^3 - 3) + 3·a^3·(b·(5·ρ^8 + 2) + 2·ρ) + 2·a^2·ρ^6·(5·ρ^3 - 2) - 3·a·ρ·(b^2 - b·ρ^9 - ρ^2) + ρ^8·(2·ρ^3 - 1))/(ρ·(a^2 + ρ^2)^5) $
Qualcuno conosce un software che possa risolvere una cosa del genere ?
A chi potrà aiutarmi farò inviare un volume a scelta dell'Opera di Corrado Brogi (mio padre) che ho recentemente pubblicato su Amazon. Purtroppo io non sono un matematico ma un informatico, il motivo per cui mi interesso di questo genere di equazioni è perché hanno una corrispondenza con i flussi di quelle che si chiamano "energie sottili".
ho iniziato a scrivere una prima bozza di studio. Mi sono fermato sconcertato dal numero di grafici diversissimi fra loro ottenibili dalla formula k=a+sin(s/b) . Qui ho riportato solo alcuni esempi http://www.giovannibrogi.it/varie/studiocurvatura.pdf
Ho aggiornato il file http://www.giovannibrogi.it/varie/studiocurvatura.pdf
Pensavo che la lemniscata di Bernoulli avesse, agli estremi, una curvatura superiore alla mia. [strike]In realtà è il contrario.[/strike]
(*) Infatti la lemniscata di Bernoulli HA una curvatura agli estremi leggermente superiore. L'errore era dovuto al programma grafico di disegno che disegnava con una curvatura doppia.
Pensavo che la lemniscata di Bernoulli avesse, agli estremi, una curvatura superiore alla mia. [strike]In realtà è il contrario.[/strike]
(*) Infatti la lemniscata di Bernoulli HA una curvatura agli estremi leggermente superiore. L'errore era dovuto al programma grafico di disegno che disegnava con una curvatura doppia.
--- ERRATA CORRIGE ---
Chiedo scusa a chi dovesse aver letto questo studio:
ho modificato il documento sul mio sito e anche le immagini ma alcune devono essere state memorizzate nel Blog.
a causa di un errore nel programma grafico, tutte le curvature erano state raddoppiate.
pertanto il numero che chiude la lemniscata su se stessa non è 4.80965 ma la metà: 2.40482557
Ne deriva che la curvatura massima della lemniscata di Bernoulli è SUPERIORE a quella della "mia" lemniscata
in questa immagine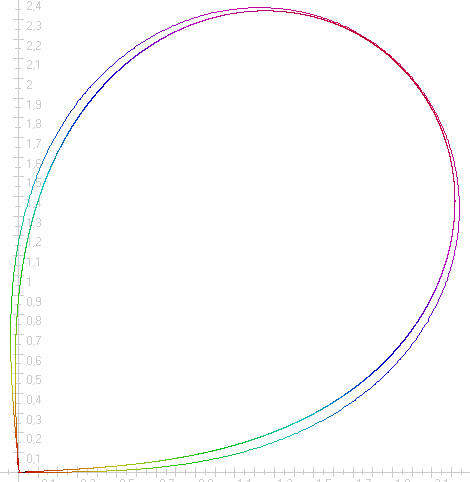
la lemniscata di Bernoulli, ruotata sullo stesso asse della mia, è disegnata all'interno. le sfumature di colore sono proporzionali alla curvatura.
Chiedo scusa a chi dovesse aver letto questo studio:
ho modificato il documento sul mio sito e anche le immagini ma alcune devono essere state memorizzate nel Blog.
a causa di un errore nel programma grafico, tutte le curvature erano state raddoppiate.
pertanto il numero che chiude la lemniscata su se stessa non è 4.80965 ma la metà: 2.40482557
Ne deriva che la curvatura massima della lemniscata di Bernoulli è SUPERIORE a quella della "mia" lemniscata
in questa immagine
la lemniscata di Bernoulli, ruotata sullo stesso asse della mia, è disegnata all'interno. le sfumature di colore sono proporzionali alla curvatura.
Oramai che ho iniziato questo post, condivido anche la soluzione che ho trovato anche se per adesso solo empiricamente: il numero 2.4048255... è la prima soluzione della funzione di Bessel, chiamata j0(x).
Che, in questo caso, corrisponde alla lunghezza 2*pigreco*S di una lemniscata di equazione k=sin(s/j0(x)) oppure k=cos(s/j0(x)).
Fra l'altro tutte le radici della funzione di Bessel, generano una lemniscata ma ad ogni radice si aggiunge un cerchietto che forma un piccolo occhio all'interno di ciascun lemnisco.
Che, in questo caso, corrisponde alla lunghezza 2*pigreco*S di una lemniscata di equazione k=sin(s/j0(x)) oppure k=cos(s/j0(x)).
Fra l'altro tutte le radici della funzione di Bessel, generano una lemniscata ma ad ogni radice si aggiunge un cerchietto che forma un piccolo occhio all'interno di ciascun lemnisco.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo