Convergenza puntuale ed in media
Salve. Sono in cerca di alcuni chiarimenti in merito ad alcuni tipi di convergenza delle successioni di funzioni, in particolare ai legami tra convergenza puntuale ed in $L^1$.
Con qualche ragionamento penso di aver raggiunto un equivalenza dei due tipi di convergenza nel caso di funzioni limitate, procedendo come segue:
1) Sia $f_j$ puntualmente convergente in $D$ ad $f$. Allora $f_j$ è quasi ovunque uniformemente convergente ad $f$, nel senso che $AA \epsilon>0 EE N in NN$ e un insieme misurabile $A sub D$ con misura minore di $\epsilon$ tale che $AA x in D\\A$ si ha $|f_j(x) - f(x)|<\epsilon AA j>=N$.
Allora ho che $||f-f_j||_1 = int_D |f-f_j| = int_A |f-f_j| + int_(D\\A) |f-f_j|$
Nel caso $f$ e tutte le $f_j$ siano dominate da un $M$, e considerando che in $D\\A$ si ha convergenza uniforme, ho dunque che
$||f-f_j||_1 < \epsilon(M+\mu(D\\A))$ (dove ho denotato con $\mu$ la misura) e dunque $f_j$ converge in $L^1$ ad $f$.
2) Sia ora $f_j$ convergente in $L^1$ ad $f$. Questo significa che $lim_(j->oo) int_D |f-f_j| = 0$. Definisco allora $g_j(x) = |f(x)-f_j(x)|$. Ho ora $lim_(j->oo) int_D g_j =0$. D'altra parte se $f$ ed $f_j$ sono dominate da $M$ tale è anche $g_j$, per cui ho passaggio del limite sotto il segno di integrale, e $int_D g(x)dx = 0$ con $g(x) = lim_(j->oo) g_j(x)$. Questo significa che $g$ è quasi ovunque nulla e $lim_(j->oo) |f(x)-f_j(x)| = 0$ vera q.o., per cui $f_j$ è q.o. uniformemente convergente ad $f$.
Le questioni sono:
i) ciò che ho scritto ha senso od ho commesso qualche (parecchi) errore di ragionamento?
ii) si hanno risultati analoghi più generali?
Grazie
Con qualche ragionamento penso di aver raggiunto un equivalenza dei due tipi di convergenza nel caso di funzioni limitate, procedendo come segue:
1) Sia $f_j$ puntualmente convergente in $D$ ad $f$. Allora $f_j$ è quasi ovunque uniformemente convergente ad $f$, nel senso che $AA \epsilon>0 EE N in NN$ e un insieme misurabile $A sub D$ con misura minore di $\epsilon$ tale che $AA x in D\\A$ si ha $|f_j(x) - f(x)|<\epsilon AA j>=N$.
Allora ho che $||f-f_j||_1 = int_D |f-f_j| = int_A |f-f_j| + int_(D\\A) |f-f_j|$
Nel caso $f$ e tutte le $f_j$ siano dominate da un $M$, e considerando che in $D\\A$ si ha convergenza uniforme, ho dunque che
$||f-f_j||_1 < \epsilon(M+\mu(D\\A))$ (dove ho denotato con $\mu$ la misura) e dunque $f_j$ converge in $L^1$ ad $f$.
2) Sia ora $f_j$ convergente in $L^1$ ad $f$. Questo significa che $lim_(j->oo) int_D |f-f_j| = 0$. Definisco allora $g_j(x) = |f(x)-f_j(x)|$. Ho ora $lim_(j->oo) int_D g_j =0$. D'altra parte se $f$ ed $f_j$ sono dominate da $M$ tale è anche $g_j$, per cui ho passaggio del limite sotto il segno di integrale, e $int_D g(x)dx = 0$ con $g(x) = lim_(j->oo) g_j(x)$. Questo significa che $g$ è quasi ovunque nulla e $lim_(j->oo) |f(x)-f_j(x)| = 0$ vera q.o., per cui $f_j$ è q.o. uniformemente convergente ad $f$.
Le questioni sono:
i) ciò che ho scritto ha senso od ho commesso qualche (parecchi) errore di ragionamento?
ii) si hanno risultati analoghi più generali?
Grazie
Risposte
C'è qualcosa che non va, si. La 2) in particolare è proprio falsa. Prendi la successione typewriter:
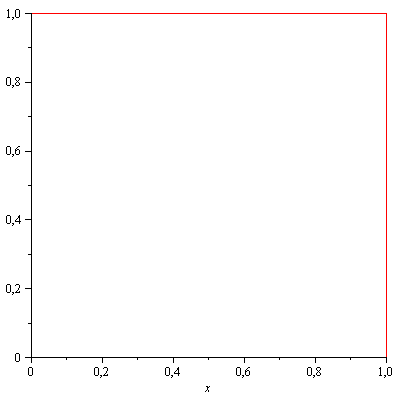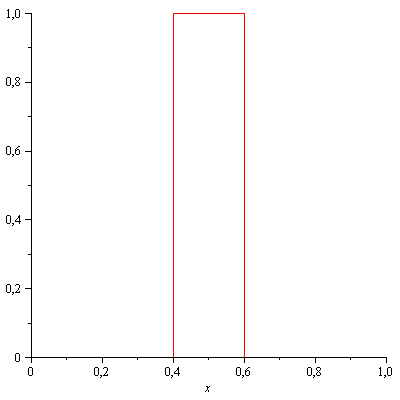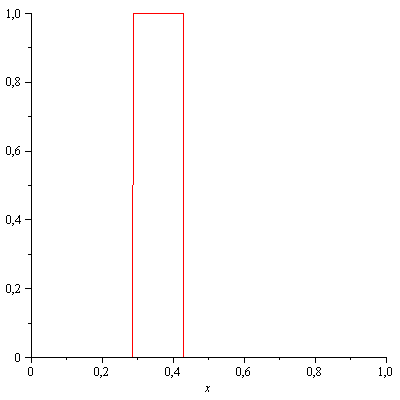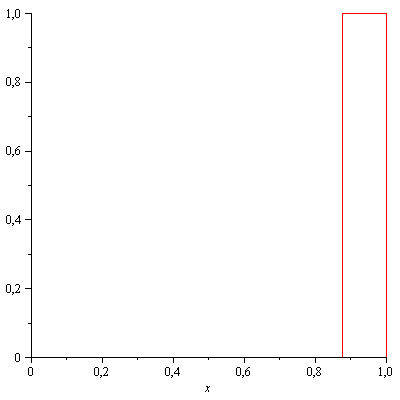
Essa converge nel senso di \(L^1\) ma certamente non converge puntualmente in nessun punto. Il baco sta nell'aver applicato "al contrario" il teorema della convergenza dominata: tu sai che \(\lim_{j \to \infty} \int g_j\, dx=0\) e non puoi risalire da questo alla convergenza puntuale. Eventualmente potresti fare il contrario: se sapessi che \(g_j\) converge puntualmente ed è dominata, allora convergerebbe pure la successione degli integrali.
Anche la 1) è falsa, a meno che non si assuma di essere in uno spazio di misura finita. Un esempio è la successione
\[f_j(x)=\chi_{[j, j+1]}(x), \qquad x \in \mathbb{R}.\]
Essa converge puntualmente ovunque ma non converge nel senso di \(L^1(\mathbb{R})\).

Essa converge nel senso di \(L^1\) ma certamente non converge puntualmente in nessun punto. Il baco sta nell'aver applicato "al contrario" il teorema della convergenza dominata: tu sai che \(\lim_{j \to \infty} \int g_j\, dx=0\) e non puoi risalire da questo alla convergenza puntuale. Eventualmente potresti fare il contrario: se sapessi che \(g_j\) converge puntualmente ed è dominata, allora convergerebbe pure la successione degli integrali.
Anche la 1) è falsa, a meno che non si assuma di essere in uno spazio di misura finita. Un esempio è la successione
\[f_j(x)=\chi_{[j, j+1]}(x), \qquad x \in \mathbb{R}.\]
Essa converge puntualmente ovunque ma non converge nel senso di \(L^1(\mathbb{R})\).
Aggiungo a questa discussione il contributo di gugo82. Buona lettura.
***
***
- [*:27xj7x2z] In generale, ossia per uno spazio di misura arbitrario, valgono le seguenti relazioni:
\[
\begin{split}
\text{q.o.} & \Leftarrow & \text{q.u.} \\
\uparrow & \nwarrow & \Downarrow \uparrow \\
L^p & \Rightarrow & \text{mis.}
\end{split}
\]
in cui ovviamente \(\text{q.o.}\) sta per "quasi ovunque", \(\text{q.u.}\) per "quasi uniforme", \(L^p\) per "convergenza in media d'ordine \(p\)" e \(\text{mis.}\) per "convergenza in misura"; ed inoltre la freccia "doppia" \(A\Rightarrow B\) significa che una successione convergente nel modo \(A\) converge anche nel modo \(B\) (e.g. una successione convergente in \(L^p\) converge anche in misura), mentre la freccia "sottile" \(A\to B\) significa che una successione convergente nel modo \(A\) possiede una sottosuccessione convergente nel modo \(B\) (e.g. una successione convergente in misura ha una sottosuccessione convergente q.o.).
[/*:m:27xj7x2z]
[*:27xj7x2z] Se lo spazio di misura ha misura finita, allora al precedente schema si aggiungono le relazioni:
\[
\begin{split}
\text{q.o.} & \Rightarrow & \text{q.u.} &\qquad \text{(teorema di Egorov)} \\
\text{q.o.} & \Rightarrow & \text{mis.} &
\end{split}
\]
[/*:m:27xj7x2z]
[*:27xj7x2z] Infine, se lo spazio di misura è arbitrario ma la convergenza è dominata in \(L^p\) (ossia se esiste una funzione positiva \(\phi \in L^p\) che maggiora q.o. i moduli degli elementi della successione assegnata), vanno aggiunte le seguenti relazioni:
\[
\begin{split}
\text{q.o.} & \Rightarrow & \text{q.u.} & \\
\text{q.o.} & \Rightarrow & \text{mis.} & \\
\text{q.o.} & \Rightarrow & L^p &\qquad \text{(teorema di convergenza dominata)} \\
\text{q.u.} & \Rightarrow & L^p & \\
L^p & \Leftarrow & \text{mis.} &
\end{split}
\][/*:m:27xj7x2z][/list:u:27xj7x2z]
***
(Una noticina mia: nell'ultimo punto si assume implictamente che \(1 \le p < \infty\).
Grazie per la risposta.
Certo che le funzioni sanno essere proprio strane .
.
i)In particolare la funzione che hai citato, la "typewriter", sarebbe una successione di funzioni caratteristiche di sottointervalli di (0,1) sempre più piccoli? Ad esempio sarebbe plausibile come candidata questa funzione?
$f_j(x) = \chi_(A_j)(x)$ con $A_j = (\sigma(j/N),\sigma(j/N)+1/(j+N))$ denotando con $\sigma(x)$ la parte non intera di $x$.
ii)Per la uno intendi che deve essere finito il dominio delle $f_j$ e di $f$? In effetti l'avevo dato per scontato ma a pensarci è fondamentale per la quasi uniforme convergenza!
iii)Riguardo poi allo "schemetto" sulle relazioni tra le convergenze... adesso provo (tento ) ad abbozzarmi qualche dimostrazione, ma intanto qualche chiarimento:
) ad abbozzarmi qualche dimostrazione, ma intanto qualche chiarimento:
a)per convergenza q.o. si intende convergenza puntuale q.o.?
b)per q.u. si intende la quasi convergenza uniforme nel senso che ho scritto nel primo post?
c)per convergenza in misura che si intende?
Grazie
Certo che le funzioni sanno essere proprio strane
 .
.i)In particolare la funzione che hai citato, la "typewriter", sarebbe una successione di funzioni caratteristiche di sottointervalli di (0,1) sempre più piccoli? Ad esempio sarebbe plausibile come candidata questa funzione?
$f_j(x) = \chi_(A_j)(x)$ con $A_j = (\sigma(j/N),\sigma(j/N)+1/(j+N))$ denotando con $\sigma(x)$ la parte non intera di $x$.
ii)Per la uno intendi che deve essere finito il dominio delle $f_j$ e di $f$? In effetti l'avevo dato per scontato ma a pensarci è fondamentale per la quasi uniforme convergenza!
iii)Riguardo poi allo "schemetto" sulle relazioni tra le convergenze... adesso provo (tento
 ) ad abbozzarmi qualche dimostrazione, ma intanto qualche chiarimento:
) ad abbozzarmi qualche dimostrazione, ma intanto qualche chiarimento:a)per convergenza q.o. si intende convergenza puntuale q.o.?
b)per q.u. si intende la quasi convergenza uniforme nel senso che ho scritto nel primo post?
c)per convergenza in misura che si intende?
Grazie
i) Sull'idea della successione typewriter hai ragione: è infatti una successione di funzioni il cui grafico è rettangolare e sottende un'area sempre più piccina, ma che non converge puntualmente in nessun punto. Perciò c'è convergenza \(L^1\) verso la funzione nulla ma non c'è convergenza puntuale, nemmeno in senso "quasi ovunque".
ii) Esatto. Questo è il teorema di Egorov citato al secondo punto del post di Gugo.
iii) a) Si; b) Si; c) Una successione di funzioni \(f_j\) definita in uno spazio di misura \(\Omega\) converge in misura verso una funzione \(f\) se
\[\forall \varepsilon >0,\ \text{mis}\Big(\{\omega \in \Omega \mid \lvert f_j(\omega)-f(\omega) \rvert > \varepsilon\}\Big) \to 0\quad \text{quando}\ j \to \infty.\]
E' un concetto che si usa soprattutto in probabilità. Si parla in questo caso di convergenza in probabilità.
ii) Esatto. Questo è il teorema di Egorov citato al secondo punto del post di Gugo.
iii) a) Si; b) Si; c) Una successione di funzioni \(f_j\) definita in uno spazio di misura \(\Omega\) converge in misura verso una funzione \(f\) se
\[\forall \varepsilon >0,\ \text{mis}\Big(\{\omega \in \Omega \mid \lvert f_j(\omega)-f(\omega) \rvert > \varepsilon\}\Big) \to 0\quad \text{quando}\ j \to \infty.\]
E' un concetto che si usa soprattutto in probabilità. Si parla in questo caso di convergenza in probabilità.
Posto il seguito della discussione con gugo82 nel caso qualcuno fosse interessato all'argomento 
[size=110]gugo82[/size]
Ciao Kyl.
Chiarisco un po' la terminologia usata qui: Titolo: Convergenza puntuale ed in media
Per la domanda (a), la risposta è sì, ovviamente.
Per le altre due, ti ricordo queste due definizioni:
Nota che la convergenza \(\text{q.u.}\) ora definita è distinta dalla convergenza uniforme quasi ovunque: quest'ultima si verifica quando esiste un insieme misurabile \(N\subseteq X\) tale che \(\mu(N)=0\) ed \((f_n)\) converge uniformemente verso \(f\) in \(X\setminus N\).
Inoltre, nota che la convergenza in misura \(\text{mis.}\) coincide con quella che i probabilisti chiamano convergenza in probabilità quando la \(\mu\) è una misura di probabilità.
Un libro dove puoi trovare queste cose è il Kolmogorov-Fomin; ma credo che queste questioni siano affrontate anche su altri libri riguardanti la teoria dell'integrazione di Lebesgue (ad esempio, mi pare che sul Bartle, Elements of Integration, ci sia uno schema analogo a quello riportato nel thread).
[size=110]Kyl[/size]
(...) Riguardo alla distinzione che mi hai fatto tra convergenza q.u. e convergenza uniforme q.o., correggimi se sbaglio, è dovuta al fatto che per la prima l'insieme in cui non si ha conv. unif. "rimpicciolisce insieme" all'avvicinarsi della successione al limite, mentre nella seconda insieme a condizione di convergenza uniforme vanno a zero indipendentemente?
Avresti qualche esempio di funzioni convergenti in uno dei due modi e non nell'altro?
[size=110]gugo82[/size]
Chiaramente la convergenza uniforme q.o. implca la convergenza q.u. (con le notazioni del PM precedente, basta prendere \(E=N\)); però in generale non vale il viceversa. Usando le notazioni del diagrammino possiamo dire che risulta:
\[\text{convergenza unif. q.o.}\ \Rightarrow\ \text{convergenza q.u.}\]
\[\text{convergenza unif. q.o.}\ \not\Leftarrow\ \text{convergenza q.u.}\]
come si vede dall'esempio che segue.
L'esempio mostra che in generale si ha pure (sempre con le notazioni del diagrammino):
\[\text{convergenza unif. q.o.}\ \not\leftarrow\ \text{convergenza q.u.}\; ,\]
quindi la convergenza uniforme q.o. non si può "recuperare" da quella q.u. nemmeno passando ad una sottosuccessione.
Una successione convergente uniformemente q.o. si può ottenere come segue.
Gli esempi sono inventati all'impronta, quindi controllali per bene e fammi sapere se ci sono errori.
[...]
P.S.: Un altro esempio di successione convergente q.u. ma non convergente uniformemente q.o. è quello fornito dalle somme parziali della serie geometrica in \([-1,1]\).
[size=110]Kyl[/size]
Dunque:
Il tuo primo esempio se ho capito la successione è praticamente la funzione $1/x$ in $[0,1]$ "troncata" in intervallini sull'origine sempre più piccoli e sostituita con una funzione costantemente uguale al valore che avrebbe altrimenti assunto $1/x$ nel punto. Quindi $f_j$ è anche una funzione $C^0$ in $[0,1] AAj in NN$ giusto? Questa successione non è q.o. unif. conv. perché per qualunque $NinNN$ arbitrariamente grande (e corrispondentemente l'intervallo sull'origine in cui $f_j$ è continua arbitrariamente piccolo) ci saranno sempre dei punti ancora più vicini all'origine in cui $f(x)$ assume valori sempre più grandi mentre $f_j(x)$ si mantiene costante al valore in cui avviene il "troncamento".
Non so se quello che ho detto è comprensibile, ho cercato di tradurre in termini intuitivi lo sfondo formale della cosa!
Per la successione delle somme parziali il ragionamento è simile con "punti problematici" -1 e 1.
Per vedere se ho capito propongo ora io una successione convergente q.u. non q.o. uniformemente convergente!
$f_n(x) = \chi_(A_n)(x)$ con $A_n = [-1/n,1/n]$ e $x in [-1,1]$
Giusto?
Quindi diciamo che in termini intuitivi la distinzione tra i due tipi di "quasi" convergenza è che per la q.o. unif. conv. l'insieme in cui non si ha unif. conv. si può scegliere arbitrariamente piccolo in modo indipendente dall'indice della successione in cui "ci si trova", mentre per la conv. q.u. l'insieme si può prendere piccolo a piacere ma a patto che si "proceda" abbastanza nella successione di funzioni.

[size=110]gugo82[/size]
Ciao Kyl.
Chiarisco un po' la terminologia usata qui: Titolo: Convergenza puntuale ed in media
"Kyl":
iii)Riguardo poi allo "schemetto" sulle relazioni tra le convergenze... adesso provo (tento) ad abbozzarmi qualche dimostrazione, ma intanto qualche chiarimento:
a)per convergenza q.o. si intende convergenza puntuale q.o.?
b)per q.u. si intende la quasi convergenza uniforme nel senso che ho scritto nel primo post?
c)per convergenza in misura che si intende?
Per la domanda (a), la risposta è sì, ovviamente.
Per le altre due, ti ricordo queste due definizioni:
Siano \((X,\mu)\) uno spazio di misura, \((f_n)\) una successione di funzioni misurabili ed \(f\) una funzione misurabile.
1. Si dice che \((f_n)\) converge quasi uniformemente (\(\text{q.u.}\)) verso \(f\) se per ogni \(\varepsilon >0\) esiste un misurabile \(E\subseteq X\) tale che \(\mu(E)<\varepsilon\) e \((f_n)\) converge uniformemente ad \(f\) in \(X\setminus E\).
2. Si dice che \((f_n)\) converge in misura (\(\text{mis.}\)) verso \(f\) se per ogni \(\varepsilon >0\) si ha \(\lim_n \mu (\{ x\in X:\ |f_n(x)-f(x)|\geq \varepsilon\}) =0\).
Nota che la convergenza \(\text{q.u.}\) ora definita è distinta dalla convergenza uniforme quasi ovunque: quest'ultima si verifica quando esiste un insieme misurabile \(N\subseteq X\) tale che \(\mu(N)=0\) ed \((f_n)\) converge uniformemente verso \(f\) in \(X\setminus N\).
Inoltre, nota che la convergenza in misura \(\text{mis.}\) coincide con quella che i probabilisti chiamano convergenza in probabilità quando la \(\mu\) è una misura di probabilità.
Un libro dove puoi trovare queste cose è il Kolmogorov-Fomin; ma credo che queste questioni siano affrontate anche su altri libri riguardanti la teoria dell'integrazione di Lebesgue (ad esempio, mi pare che sul Bartle, Elements of Integration, ci sia uno schema analogo a quello riportato nel thread).
[size=110]Kyl[/size]
(...) Riguardo alla distinzione che mi hai fatto tra convergenza q.u. e convergenza uniforme q.o., correggimi se sbaglio, è dovuta al fatto che per la prima l'insieme in cui non si ha conv. unif. "rimpicciolisce insieme" all'avvicinarsi della successione al limite, mentre nella seconda insieme a condizione di convergenza uniforme vanno a zero indipendentemente?
Avresti qualche esempio di funzioni convergenti in uno dei due modi e non nell'altro?
[size=110]gugo82[/size]
"Kyl":
Riguardo alla distinzione che mi hai fatto tra convergenza q.u. e convergenza uniforme q.o., correggimi se sbaglio, è dovuta al fatto che per la prima l'insieme in cui non si ha conv. unif. "rimpicciolisce insieme" all'avvicinarsi della successione al limite, mentre nella seconda insieme a condizione di convergenza uniforme vanno a zero indipendentemente?
Avresti qualche esempio di funzioni convergenti in uno dei due modi e non nell'altro?
Chiaramente la convergenza uniforme q.o. implca la convergenza q.u. (con le notazioni del PM precedente, basta prendere \(E=N\)); però in generale non vale il viceversa. Usando le notazioni del diagrammino possiamo dire che risulta:
\[\text{convergenza unif. q.o.}\ \Rightarrow\ \text{convergenza q.u.}\]
\[\text{convergenza unif. q.o.}\ \not\Leftarrow\ \text{convergenza q.u.}\]
come si vede dall'esempio che segue.
L'esempio mostra che in generale si ha pure (sempre con le notazioni del diagrammino):
\[\text{convergenza unif. q.o.}\ \not\leftarrow\ \text{convergenza q.u.}\; ,\]
quindi la convergenza uniforme q.o. non si può "recuperare" da quella q.u. nemmeno passando ad una sottosuccessione.
Una successione convergente uniformemente q.o. si può ottenere come segue.
Gli esempi sono inventati all'impronta, quindi controllali per bene e fammi sapere se ci sono errori.
[...]
P.S.: Un altro esempio di successione convergente q.u. ma non convergente uniformemente q.o. è quello fornito dalle somme parziali della serie geometrica in \([-1,1]\).
[size=110]Kyl[/size]
Dunque:
Il tuo primo esempio se ho capito la successione è praticamente la funzione $1/x$ in $[0,1]$ "troncata" in intervallini sull'origine sempre più piccoli e sostituita con una funzione costantemente uguale al valore che avrebbe altrimenti assunto $1/x$ nel punto. Quindi $f_j$ è anche una funzione $C^0$ in $[0,1] AAj in NN$ giusto? Questa successione non è q.o. unif. conv. perché per qualunque $NinNN$ arbitrariamente grande (e corrispondentemente l'intervallo sull'origine in cui $f_j$ è continua arbitrariamente piccolo) ci saranno sempre dei punti ancora più vicini all'origine in cui $f(x)$ assume valori sempre più grandi mentre $f_j(x)$ si mantiene costante al valore in cui avviene il "troncamento".
Non so se quello che ho detto è comprensibile, ho cercato di tradurre in termini intuitivi lo sfondo formale della cosa!
Per la successione delle somme parziali il ragionamento è simile con "punti problematici" -1 e 1.
Per vedere se ho capito propongo ora io una successione convergente q.u. non q.o. uniformemente convergente!
$f_n(x) = \chi_(A_n)(x)$ con $A_n = [-1/n,1/n]$ e $x in [-1,1]$
Giusto?
Quindi diciamo che in termini intuitivi la distinzione tra i due tipi di "quasi" convergenza è che per la q.o. unif. conv. l'insieme in cui non si ha unif. conv. si può scegliere arbitrariamente piccolo in modo indipendente dall'indice della successione in cui "ci si trova", mentre per la conv. q.u. l'insieme si può prendere piccolo a piacere ma a patto che si "proceda" abbastanza nella successione di funzioni.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo