Convergenza integrali
Ciao a tutti...
Se qualcuno mi risolvesse in modo chiaro ed esplicito questi esercizi gli sarei grato... Ho bisogno di individuare una traccia più generale di certi tipi di esercizi...!!
1.$int_{1}^{+ \infty} ((lnx)^a)/((1+x^2)^b) dx$ a,b $\in$ R
Discutere la convergenza dell'integrale.
2. $int_{0}^{+ \infty} x^a e^(-x) dx$ a $\in$ R
Determinare per quali a l'integrale converge.
Vi ringrazio!
Paola
Se qualcuno mi risolvesse in modo chiaro ed esplicito questi esercizi gli sarei grato... Ho bisogno di individuare una traccia più generale di certi tipi di esercizi...!!
1.$int_{1}^{+ \infty} ((lnx)^a)/((1+x^2)^b) dx$ a,b $\in$ R
Discutere la convergenza dell'integrale.
2. $int_{0}^{+ \infty} x^a e^(-x) dx$ a $\in$ R
Determinare per quali a l'integrale converge.
Vi ringrazio!
Paola
Risposte
Per l'esercizio $2$ l'integrale dovrebbe essere assolutamente convergente per $a > -1$... infatti:
1)In un intorno destro di $0$:
- per $a<-1$ la funzione $x^a e^(-x)$ è minorata dalla funzione $1/(2x)$ che non è sommabile;
- per $-1
2)Intorno a $+oo$ invece la funzione $e^(-x)$ è infinitesima di ordine infinitamente grande
1)In un intorno destro di $0$:
- per $a<-1$ la funzione $x^a e^(-x)$ è minorata dalla funzione $1/(2x)$ che non è sommabile;
- per $-1
2)Intorno a $+oo$ invece la funzione $e^(-x)$ è infinitesima di ordine infinitamente grande
Allora
comincerò anche io dal secondo integrale in quanto mi è in un certo senso ‘familiare’. Per prima cosa chiedo a prime_number il permesso di poter cambiare il nome alle variabili e di scrivere l’integrale in questo modo …
$int_0^(+oo) t^x*e^(-t)*dt$ (1)
Si chiede per quali valori di $x$ l’integrale converge. Benissimo!… Nel topic da me ‘momentaneamente trascurato’ [ma che conto di riprendere quanto prima…] Giusto per ridere un poco prime-number può leggere il seguente post…
https://www.matematicamente.it/f/viewtop ... 2452#76151
… nel quale è introdotta la ‘funzione gamma minuscola’ definita come…
$gamma(x)= int_0^(+oo) t^x*e^(-t)*dt$ (2)
... cioè proprio l’integrale (1). Tra le varie proprietà della funzione che lì vengono ricavate, particolarmente importanti sono le due seguenti …
$gamma (x+1)= (x+1)*gamma (x)$ (3)
$gamma (x-1)= (gamma(x))/x$ (4)
… chiamate rispettivamente ‘estensione in avanti’ ed ‘estensione all’indietro’. Esse permettono, una volta nota la funzione in $(-.5,.5)$ il calcolo della stessa per qualunque valore di $x$. Per $x=n$ con $n$ intero non negativo vale il noto risultato…
$gamma(n)=n!$ (5)
In base alla (3) possiamo dire che l’integrale converge per tutte le $x>0$. In base alla (4) possiamo concludere che l’integrale converge per tutti i valori di $x<0$… tranne quando $x$ è un intero negativo. Ponendo infatti nella (4) $x=0$ si vede che l’integrale diverge per $x=-1$ e, sempre per la (4), per ogni altro intero negativo.
Il quesito relativo al secondo integrale dovrebbe essere quindi risolto. Per quanto riguarda il primo integrale propostoci da prime_number ci vediamo più tardi…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
comincerò anche io dal secondo integrale in quanto mi è in un certo senso ‘familiare’. Per prima cosa chiedo a prime_number il permesso di poter cambiare il nome alle variabili e di scrivere l’integrale in questo modo …
$int_0^(+oo) t^x*e^(-t)*dt$ (1)
Si chiede per quali valori di $x$ l’integrale converge. Benissimo!… Nel topic da me ‘momentaneamente trascurato’ [ma che conto di riprendere quanto prima…] Giusto per ridere un poco prime-number può leggere il seguente post…
https://www.matematicamente.it/f/viewtop ... 2452#76151
… nel quale è introdotta la ‘funzione gamma minuscola’ definita come…
$gamma(x)= int_0^(+oo) t^x*e^(-t)*dt$ (2)
... cioè proprio l’integrale (1). Tra le varie proprietà della funzione che lì vengono ricavate, particolarmente importanti sono le due seguenti …
$gamma (x+1)= (x+1)*gamma (x)$ (3)
$gamma (x-1)= (gamma(x))/x$ (4)
… chiamate rispettivamente ‘estensione in avanti’ ed ‘estensione all’indietro’. Esse permettono, una volta nota la funzione in $(-.5,.5)$ il calcolo della stessa per qualunque valore di $x$. Per $x=n$ con $n$ intero non negativo vale il noto risultato…
$gamma(n)=n!$ (5)
In base alla (3) possiamo dire che l’integrale converge per tutte le $x>0$. In base alla (4) possiamo concludere che l’integrale converge per tutti i valori di $x<0$… tranne quando $x$ è un intero negativo. Ponendo infatti nella (4) $x=0$ si vede che l’integrale diverge per $x=-1$ e, sempre per la (4), per ogni altro intero negativo.
Il quesito relativo al secondo integrale dovrebbe essere quindi risolto. Per quanto riguarda il primo integrale propostoci da prime_number ci vediamo più tardi…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Per curiosità, sommabilità = integrabilità in senso improprio?
Non avevo mai sentito il termine "sommabile".
Non avevo mai sentito il termine "sommabile".
Per il primo integrale, si ricordi che vale la disuguaglianza:
$0 <= logx <= x " " AAx >=1$
Se $a>=0$, allora possiamo maggiorare l'integranda
con la funzione $(x^a)/(1+x^2)^b$ in quanto la
funzione $(lnx)^a$ risulta crescente sotto quest'ipotesi.
Si noti inoltre che la funzione
maggiorante risulta definitivamente positiva per $x->+oo$,
per cui basta determinare il suo ordine di infinitesimo.
Per $x->+oo$ si ha:
$(x^a)/(x^2 ( 1+ o(1)) )^b = (x^a)/(x^(2b) (1+ o(1)) )= x^(a-2b) (1+o(1))= 1/(x^(2b-a)) (1+o(1))
ossia, la funzione $(x^a)/(1+x^2)^b$ è un infinitesimo di ordine $2b-a$ per $x->+oo$.
Chiaramente per essere infinitesima la funzione, occorre che sia $2b-a>0$ ovvero $b>1/2 a$.
A questo punto ricordiamo che siamo sotto l'ipotesi $a>=0$.
Per convergere l'integrale improprio della funzione maggiorante,
occorre che l'ordine di infinitesimo sia strettamente maggiore di 1,
dunque $2b-a>1 <=> 2b > a+1 <=>b > 1/2 (a+1)
da cui possiamo dedurre che la funzione $(x^a)/(1+x^2)^b$ è
integrabile in senso improprio se $a>=0$ e $b>1/2$,
infatti $b>1/2 (a +1) >= 1/2 " " AAa>=0$.
Dall'integrabilità in senso improprio di $(x^a)/(1+x^2)^b$
segue per il criterio del confronto quella della funzione integranda.
$0 <= logx <= x " " AAx >=1$
Se $a>=0$, allora possiamo maggiorare l'integranda
con la funzione $(x^a)/(1+x^2)^b$ in quanto la
funzione $(lnx)^a$ risulta crescente sotto quest'ipotesi.
Si noti inoltre che la funzione
maggiorante risulta definitivamente positiva per $x->+oo$,
per cui basta determinare il suo ordine di infinitesimo.
Per $x->+oo$ si ha:
$(x^a)/(x^2 ( 1+ o(1)) )^b = (x^a)/(x^(2b) (1+ o(1)) )= x^(a-2b) (1+o(1))= 1/(x^(2b-a)) (1+o(1))
ossia, la funzione $(x^a)/(1+x^2)^b$ è un infinitesimo di ordine $2b-a$ per $x->+oo$.
Chiaramente per essere infinitesima la funzione, occorre che sia $2b-a>0$ ovvero $b>1/2 a$.
A questo punto ricordiamo che siamo sotto l'ipotesi $a>=0$.
Per convergere l'integrale improprio della funzione maggiorante,
occorre che l'ordine di infinitesimo sia strettamente maggiore di 1,
dunque $2b-a>1 <=> 2b > a+1 <=>b > 1/2 (a+1)
da cui possiamo dedurre che la funzione $(x^a)/(1+x^2)^b$ è
integrabile in senso improprio se $a>=0$ e $b>1/2$,
infatti $b>1/2 (a +1) >= 1/2 " " AAa>=0$.
Dall'integrabilità in senso improprio di $(x^a)/(1+x^2)^b$
segue per il criterio del confronto quella della funzione integranda.
"fireball":
Per curiosità, sommabilità = integrabilità in senso improprio?
Non avevo mai sentito il termine "sommabile".
Una funzione è sommabile in un certo intervallo se in tale intervallo il suo modulo è integrabile. La sommabilità è una proprietà più forte dell'integrabilità, dunque esistono funzioni integrabili ma non sommabili (dette "semplicemente integrabili"), mentre la sommabilità implica l'integrabilità. Ovviamente ho parlato di sommabilità in quanto $x^a e^(-x)$ è sempre positiva per $x>0$.
Ah ho capito, dunque sommabilità = assoluta integrabilità in senso improprio. Ok!
Sommabile è più un termine che si usa per l'integrale di Lebesgue, dove è praticamente d'obbligo integrare sempre il valore assoluto della funzione. A tal punto la distinzione integrale/integrale in senso improprio non ha più ragione di esistere.
Eppure lupo grigio, se prendi $a=-3/2$ la funzione $(e^(-x))/(x^(3/2))$ non è minorata dalla funzione $1/(2x)$ intorno a $0$?
Sempre per il primo integrale, se $a<0$
si ragiona in maniera analoga, tenendo
però conto che 1) si deve sfruttare la disuguaglianza
$0<=1/x^(-a)<=1/(logx)^(-a)$
valida per ogni x maggiore di 1
(essendo $-a>0$), e 2) il problema dell'integrabilità
in senso improprio (o come preferite dire,
della convergenza dell'integrale) si pone anche
per $x->1^+$ oltre che per $x->+oo$.
si ragiona in maniera analoga, tenendo
però conto che 1) si deve sfruttare la disuguaglianza
$0<=1/x^(-a)<=1/(logx)^(-a)$
valida per ogni x maggiore di 1
(essendo $-a>0$), e 2) il problema dell'integrabilità
in senso improprio (o come preferite dire,
della convergenza dell'integrale) si pone anche
per $x->1^+$ oltre che per $x->+oo$.
Se $a<0$, io ho spezzato l'integrale così:
$int_1^k f(x) dx + int_k^(+oo) f(x) dx
con $1 < k < +oo$ e il primo integrale
converge $AAa in (-1,0)$ e $AAb in RR$.
Un po' più complicato è studiare la convergenza
del secondo integrale, ovvero per $x->+oo$...
$int_1^k f(x) dx + int_k^(+oo) f(x) dx
con $1 < k < +oo$ e il primo integrale
converge $AAa in (-1,0)$ e $AAb in RR$.
Un po' più complicato è studiare la convergenza
del secondo integrale, ovvero per $x->+oo$...
Il quesito sollevato da Kroldar è del tutto giustificato. Tuttavia per approfondire la questione servirebbe un lungo e tortuoso discorso per cui diciamo che la convergenza dell’integrale…
$int_0^(+oo) t^x*e^(-t)*dt$ (1)
… è comunque garantita per $x> -1$…
La convergenza dell’altro integrale…
$int_1^(+oo) (ln^x t)/((1+t^2)^y)*dt$ (2)
… per $y>0$ può rifarsi all’integrale…
$int_1^(+oo) (ln^x t)/(t^(2*y))*dt$ (3)
Posto $u=x$ e $v=2*y$, consideriamo la funzione…
$phi(u,v)= int_1^(+oo) (ln^u t)/(t^v)*dt$ (4)
Applicando la regola di integrazione per parti abbiamo…
$phi(u,v)= int_1^(+oo) (ln^u t)/(t^v)*dt=$
$=|-(ln^u t)/((v-1)*t^(v-1))|_1^(+oo) + u/(v-1)*int_1^(+oo) (ln^(u-1) t)/(t^v)*dt=$
$=u/(v-1)*phi(u-1,v)$ (5)
In definitiva è dunque…
$phi(u-1,v)=(v-1)/u*phi(u,v)$ (6)
… o equivalentemente…
$phi(u,v)=u/(v-1)*phi(u-1,v)$ (7)
La (6) ci dice che i punti in cui è $u=-1,-2,…,-k,…$ si ha una singolarità della $phi$ e la (7) ci dice che lo stesso accade per $v=1$. Di conseguenza l’integrale (4) sarà sicuramente convergente per $u> -1$ e $v>1$, ovvero per $x> -1$ e $y>1/2$…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
$int_0^(+oo) t^x*e^(-t)*dt$ (1)
… è comunque garantita per $x> -1$…
La convergenza dell’altro integrale…
$int_1^(+oo) (ln^x t)/((1+t^2)^y)*dt$ (2)
… per $y>0$ può rifarsi all’integrale…
$int_1^(+oo) (ln^x t)/(t^(2*y))*dt$ (3)
Posto $u=x$ e $v=2*y$, consideriamo la funzione…
$phi(u,v)= int_1^(+oo) (ln^u t)/(t^v)*dt$ (4)
Applicando la regola di integrazione per parti abbiamo…
$phi(u,v)= int_1^(+oo) (ln^u t)/(t^v)*dt=$
$=|-(ln^u t)/((v-1)*t^(v-1))|_1^(+oo) + u/(v-1)*int_1^(+oo) (ln^(u-1) t)/(t^v)*dt=$
$=u/(v-1)*phi(u-1,v)$ (5)
In definitiva è dunque…
$phi(u-1,v)=(v-1)/u*phi(u,v)$ (6)
… o equivalentemente…
$phi(u,v)=u/(v-1)*phi(u-1,v)$ (7)
La (6) ci dice che i punti in cui è $u=-1,-2,…,-k,…$ si ha una singolarità della $phi$ e la (7) ci dice che lo stesso accade per $v=1$. Di conseguenza l’integrale (4) sarà sicuramente convergente per $u> -1$ e $v>1$, ovvero per $x> -1$ e $y>1/2$…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
"lupo grigio":
Il quesito sollevato da Kroldar è del tutto giustificato. Tuttavia per approfondire la questione servirebbe un lungo e tortuoso discorso per cui diciamo che la convergenza dell’integrale…
$int_0^(+oo) t^x*e(-t)*dt$ (1)
… è comunque garantita per $x> -1$…
A me però codesto lungo e tortuoso discorso interesserebbe molto... se hai tempo (e ovviamente voglia) perché non lo inizi? Ti garantisco che lo seguirò molto volentieri.
caro Kroldar
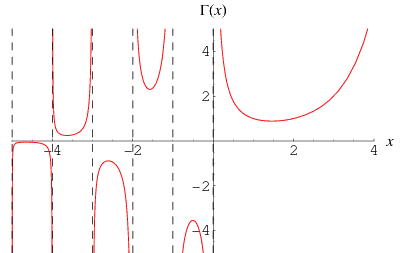
una delle più affascinanti [e controverse…] eredità lasciateci dal grande Eulero è la cosiddetta ‘Funzione Gamma’, definita come…
$Gamma(x)= int_0^(+oo) t^(x-1)*e^(-t)*dt$ (1)
Và da sè che vale l’identità…
$gamma(x)= int_0^(+oo) t^x*e^(-t)*dt = Gamma (x+1)$ (2)
Ebbene la Funzione Gamma [con la lettera maiuscola…] per $x$ reale è definita ovunque tranne che per $x=0,-1,-2,…$, dove presenta singolarità del primo ordine [con tanto di ‘residui’...]. Sul thread ‘maledetto’ Giusto per ridere un poco ho iniziato una mia personale ‘indagine’ sulla funzione gamma [con la lettera minuscola…] , indagine che conto quanto prima di riprendere [e naturalmente anche il tuo contributo sarà ben accetto...]. Intanto, già che ci siamo, sarebbe interessante sentire il parere riguardo al comportamento della $Gamma(x)$ per valori di $x$ negativi di qualche ‘mente geniale’ del forum… giusto per ridere un poco
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Ti dirò lupo grigio... la funzione Gamma l'ho già incontrata... ne faceva cenno il libro di Metodi Matematici per l'Ingegneria (esame che ho dato l'anno scorso) e ricordo anche la simpatica relazione di ricorrenza per la quale $Gamma(n+1)=n! AA n in NN$. Veniva anche detto (ed è facile verificarlo, ad esempio seguendo il ragionamento che ho fatto in merito al secondo integrale proposto da prime_number) che tale funzione è definita $AA x>0$... ecco dunque che l'integrale della domanda numero 2 è definito $AA x> -1$. Tuttavia credo (spero) di iniziare a capire cosa intendessi tu prima... quando hai detto che la funzione Gamma è definita ovunque ad eccezione dei numeri interi negativi (zero incluso) mi è venuta in mente la funzione Zeta, la quale in apparenza è definita solo per numeri reali maggiori di $1$, ma che in realtà è prolungata all'intero piano complesso!! Forse ti riferivi a un prolungamento analitico della funzione Gamma? In caso affermativo, puoi spiegarmi nella fattispecie come avviene tale prolungamento?
Un bell'esempio lo hai fornito tu stesso. Supponiamo di voler calcolare...
$gamma(-3/2)= int_0^(+oo) t^(-3/2)*e^(-t)*dt$ (1)
Partiamo con l'integrale seguente, che sappiamo convergente...
$gamma(-1/2)=int_0^(+oo) t^(-1/2)*e^(-t)*dt$ (2)
Ponendo $t=u^2$ l'integrale diviene...
$gamma (-1/2)= 2*int_0^(+oo) e^(-u^2)*du=sqrt(pi)$ (3)
Ricordando a questo punto la 'formula di estensione all'indietro'...
$gamma(x-1)=(gamma(x))/x$ (4)
... otteniamo...
$gamma(-3/2)=-(gamma(-1/2))/(1/2)=-2*sqrt(pi)$ (5)
Voilà... les jeux sont fait!...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
$gamma(-3/2)= int_0^(+oo) t^(-3/2)*e^(-t)*dt$ (1)
Partiamo con l'integrale seguente, che sappiamo convergente...
$gamma(-1/2)=int_0^(+oo) t^(-1/2)*e^(-t)*dt$ (2)
Ponendo $t=u^2$ l'integrale diviene...
$gamma (-1/2)= 2*int_0^(+oo) e^(-u^2)*du=sqrt(pi)$ (3)
Ricordando a questo punto la 'formula di estensione all'indietro'...
$gamma(x-1)=(gamma(x))/x$ (4)
... otteniamo...
$gamma(-3/2)=-(gamma(-1/2))/(1/2)=-2*sqrt(pi)$ (5)
Voilà... les jeux sont fait!...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Certo, su questo siamo d'accordo... tuttavia sorge spontanea la domanda: chi ci dice che sia lecito uscire dal dominio?
Nel senso... abbiamo definito la funzione Gamma in un certo dominio, ora il prolungamento analitico consiste semplicemente nella definizione di una nuova funzione che è identica alla funzione Gamma dove essa è definita, mentre dove essa non è definita si usa la formula di estensione all'indietro (nonostante il fatto che se si esce dal dominio di partenza l'integrale non è più assolutamente convergente)? Tutto qua? Oppure esiste una formulazione completa, magari con qualche rettifica alla funzione originaria, che rende l'integrale assolutamente convergente anche per $x< -1$?
Nel senso... abbiamo definito la funzione Gamma in un certo dominio, ora il prolungamento analitico consiste semplicemente nella definizione di una nuova funzione che è identica alla funzione Gamma dove essa è definita, mentre dove essa non è definita si usa la formula di estensione all'indietro (nonostante il fatto che se si esce dal dominio di partenza l'integrale non è più assolutamente convergente)? Tutto qua? Oppure esiste una formulazione completa, magari con qualche rettifica alla funzione originaria, che rende l'integrale assolutamente convergente anche per $x< -1$?
caro Kroldar
confesso in tutta sincerità di non essere in grado di dare una risposta soddisfacente alle 'perplessità' da te manifestate... certamente meglio di me al riguardo può fare qualche 'esperto' che qui certamente non manca...
Quello che mi è parso di capire, leggendo e sentendo anche il parere di matematici, è che la cosa importante è essere in grado di utilizzare al meglio le proprietà di funzioni 'particolari' come la 'Funzione Gamma' in quanto grazie ad esse è possibile accedere a numerose 'strade nuove'... l'aspetto puramente formale formale insomma viene in secondo piano...
Certo non tutti la pensano così... pazienza!...

cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
confesso in tutta sincerità di non essere in grado di dare una risposta soddisfacente alle 'perplessità' da te manifestate... certamente meglio di me al riguardo può fare qualche 'esperto' che qui certamente non manca...
Quello che mi è parso di capire, leggendo e sentendo anche il parere di matematici, è che la cosa importante è essere in grado di utilizzare al meglio le proprietà di funzioni 'particolari' come la 'Funzione Gamma' in quanto grazie ad esse è possibile accedere a numerose 'strade nuove'... l'aspetto puramente formale formale insomma viene in secondo piano...
Certo non tutti la pensano così... pazienza!...

cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
"lupo grigio":
Certo non tutti la pensano così... pazienza!...

Battagliero e pungente come sempre...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo