Chiarimenti sui casi di non derivabilità

[Gmork]

Salve,

volevo maggiori chiarimenti riguardanti i casi in cui una funzione non risulta derivabile in alcuni punti, per esempio:

se $\lim_{x\to x_0^-} f'(x)=l\in \mathbb{R}$ ; $\lim_{x\to x_0^+} f'(x)=\pm \infty$ , oppure: se $\lim_{x\to x_0^+} f'(x)=l\in \mathbb{R}$ ; $\lim_{x\to x_0^-} f'(x)=\pm \infty$
Si può ancora parlare di cuspide?

[pater46]

Si parla di cuspide quando il limite del rapporto incrementale da destra vale $+oo$ e da sinistra vale $-oo$ oppure viceversa...

I casi cui fai riferimento tu sono propri dei punti angolosi, nei quali almeno uno dei due è un limite finito.

[Gmork]

Graficamente come li rappresento visto che di solito quando si è in presenza di punti angolosi i due limiti non sono uguali ma sono finiti?

[pater46]

beh, per $m -> + oo$ una generica retta $ y=mx +q$ "impenna", tanto per farti rendere l'idea, diventa sempre più parallela all'asse delle ordinate.

Idem per il comportamento di una funzione... Ad esempio in questa immagine:

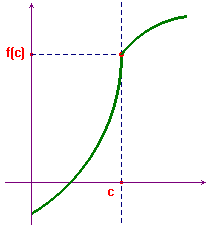
hai:

$lim_{x->x_0^-} f(x) = +oo$ mentre $lim_{x->x_0^+} f(x) = l \in RR$... una situazione come quella che hai descritto tu prima

[Gmork]

Però alla sinistra una somiglianza con una cuspide c'è o mi sbaglio?

[pater46]

Si certo, infatti a sinistra il rapporto incrementale tende a $+ oo$, come nel caso di una cuspide.

L'unica differenza tra una cuspide ed un punto angoloso è che in quest'ultimo caso almeno uno dei due limite è finito.

[Gmork]

Ok. Capito. Grazie