Posizione Lessicografica
Data una lista , di n elementi non ripetuti,come si determina il suo posto nell'insieme di tutte le liste possibili di permutazione generarte in ordine lessicografico?
eugenio
eugenio
Risposte
Facci un esempio per cortesia
Lord K grazie per la tua disponibilità.
allora:
se prendo una lista di 5 elementi ad es. (1,2,3,4,5) posso scrivere l' elenco di tutte le permutazioni possibili in ordine lessicografico.:
1 [1, 2, 3, 4, 5]
2 [1, 2, 3, 5, 4]
3 [1, 2, 4, 3, 5]
4 [1, 2, 4, 5, 3]
5 [1, 2, 5, 3, 4]
6 [1, 2, 5, 4, 3]
7 [1, 3, 2, 4, 5]
8 [1, 3, 2, 5, 4]
9 [1, 3, 4, 2, 5]
10 [1, 3, 4, 5, 2]
11 [1, 3, 5, 2, 4]
12 [1, 3, 5, 4, 2]
13 [1, 4, 2, 3, 5]
14 [1, 4, 2, 5, 3]
15 [1, 4, 3, 2, 5]
16 [1, 4, 3, 5, 2]
17 [1, 4, 5, 2, 3]
18 [1, 4, 5, 3, 2]
19 [1, 5, 2, 3, 4]
20 [1, 5, 2, 4, 3]
21 [1, 5, 3, 2, 4]
22 [1, 5, 3, 4, 2]
23 [1, 5, 4, 2, 3]
24 [1, 5, 4, 3, 2]
25 [2, 1, 3, 4, 5]
26 [2, 1, 3, 5, 4]
27 [2, 1, 4, 3, 5]
28 [2, 1, 4, 5, 3]
29 [2, 1, 5, 3, 4]
30 [2, 1, 5, 4, 3]
31 [2, 3, 1, 4, 5]
32 [2, 3, 1, 5, 4]
33 [2, 3, 4, 1, 5]
34 [2, 3, 4, 5, 1]
.
.
.
110 [5, 3, 1, 4, 2]
111 [5, 3, 2, 1, 4]
112 [5, 3, 2, 4, 1]
113 [5, 3, 4, 1, 2]
114 [5, 3, 4, 2, 1]
115 [5, 4, 1, 2, 3]
116 [5, 4, 1, 3, 2]
117 [5, 4, 2, 1, 3]
118 [5, 4, 2, 3, 1]
119 [5, 4, 3, 1, 2]
120 [5, 4, 3, 2, 1]
ora se prendo a caso una list ad es. [2, 1, 4, 5, 3] come faccio ha ricavarmi il post n° 28
senza che debba generare tutto l'insieme delle permutazion?
saluti eugenio
allora:
se prendo una lista di 5 elementi ad es. (1,2,3,4,5) posso scrivere l' elenco di tutte le permutazioni possibili in ordine lessicografico.:
1 [1, 2, 3, 4, 5]
2 [1, 2, 3, 5, 4]
3 [1, 2, 4, 3, 5]
4 [1, 2, 4, 5, 3]
5 [1, 2, 5, 3, 4]
6 [1, 2, 5, 4, 3]
7 [1, 3, 2, 4, 5]
8 [1, 3, 2, 5, 4]
9 [1, 3, 4, 2, 5]
10 [1, 3, 4, 5, 2]
11 [1, 3, 5, 2, 4]
12 [1, 3, 5, 4, 2]
13 [1, 4, 2, 3, 5]
14 [1, 4, 2, 5, 3]
15 [1, 4, 3, 2, 5]
16 [1, 4, 3, 5, 2]
17 [1, 4, 5, 2, 3]
18 [1, 4, 5, 3, 2]
19 [1, 5, 2, 3, 4]
20 [1, 5, 2, 4, 3]
21 [1, 5, 3, 2, 4]
22 [1, 5, 3, 4, 2]
23 [1, 5, 4, 2, 3]
24 [1, 5, 4, 3, 2]
25 [2, 1, 3, 4, 5]
26 [2, 1, 3, 5, 4]
27 [2, 1, 4, 3, 5]
28 [2, 1, 4, 5, 3]
29 [2, 1, 5, 3, 4]
30 [2, 1, 5, 4, 3]
31 [2, 3, 1, 4, 5]
32 [2, 3, 1, 5, 4]
33 [2, 3, 4, 1, 5]
34 [2, 3, 4, 5, 1]
.
.
.
110 [5, 3, 1, 4, 2]
111 [5, 3, 2, 1, 4]
112 [5, 3, 2, 4, 1]
113 [5, 3, 4, 1, 2]
114 [5, 3, 4, 2, 1]
115 [5, 4, 1, 2, 3]
116 [5, 4, 1, 3, 2]
117 [5, 4, 2, 1, 3]
118 [5, 4, 2, 3, 1]
119 [5, 4, 3, 1, 2]
120 [5, 4, 3, 2, 1]
ora se prendo a caso una list ad es. [2, 1, 4, 5, 3] come faccio ha ricavarmi il post n° 28
senza che debba generare tutto l'insieme delle permutazion?
saluti eugenio
Allora, con un poca di furbizia costruiamo la seguente funzione:
$phi:S_5 rightarrow ZZ$
dove:
$phi(a,b,c,d,e) = 24*(a-1)+6*max{0,b-2}+2*max{0,c-3}+max{0,d-4}+1$
Allora l'elemento: $sigma_0=(2,1,4,5,3)$ è al posto $phi(sigma_0) = 24*1+0+2*1+1+1 = 24+0+2+1+1=28$
Altro esempio:
$sigma_1= (5,4,3,1,2) Rightarrow phi(sigma_1)=24*4+6*3+2*2+0+1 = 119$
Il metodo per ricavarlo è stato osservare come sono disposti gli elementi e quanti ce ne sono da notare che la disposizione dipende da solo $4$ elementi
$phi:S_5 rightarrow ZZ$
dove:
$phi(a,b,c,d,e) = 24*(a-1)+6*max{0,b-2}+2*max{0,c-3}+max{0,d-4}+1$
Allora l'elemento: $sigma_0=(2,1,4,5,3)$ è al posto $phi(sigma_0) = 24*1+0+2*1+1+1 = 24+0+2+1+1=28$
Altro esempio:
$sigma_1= (5,4,3,1,2) Rightarrow phi(sigma_1)=24*4+6*3+2*2+0+1 = 119$
Il metodo per ricavarlo è stato osservare come sono disposti gli elementi e quanti ce ne sono da notare che la disposizione dipende da solo $4$ elementi
se ho capito bene la formula generale sarebbe:
n=numero elementi
VJ= valore del j-esimo elemento
(n-1)!*(V1-1)+(n-2)!*max{0,V2-2}+ ...........+ (n-n+1)!* max{0,V(n-1)-(n-1)} +1
ma i conti non mi tornano
es [4,1,3,2]
6*(4-1)+ 2*max{0,1-2}+1*max{0,3-3}+1 =18+0+0+1 =19 mentre la lista si trova in 20
dove sbaglio?
n=numero elementi
VJ= valore del j-esimo elemento
(n-1)!*(V1-1)+(n-2)!*max{0,V2-2}+ ...........+ (n-n+1)!* max{0,V(n-1)-(n-1)} +1
ma i conti non mi tornano
es [4,1,3,2]
6*(4-1)+ 2*max{0,1-2}+1*max{0,3-3}+1 =18+0+0+1 =19 mentre la lista si trova in 20
dove sbaglio?
Più probabile sbagli io 
Il mio risultato non è frutto di attento studio del problema ma di risposte d'acchito... conto comunque che l'idea possa starci, bisogna solo affinarla ancora un pochetto...
Il mio risultato non è frutto di attento studio del problema ma di risposte d'acchito... conto comunque che l'idea possa starci, bisogna solo affinarla ancora un pochetto...
scusa se ti rispondo solo adesso ma ero a lavoro e non ho potuto
ti confesso che sto su questo problema da due settimane e le mie pseudo soluzioni sono molto simili alla tua e credo che come dici tu affinado si possa risolverlo
grazie per il tuo interessamento
ciao eugenio
ti confesso che sto su questo problema da due settimane e le mie pseudo soluzioni sono molto simili alla tua e credo che come dici tu affinado si possa risolverlo
grazie per il tuo interessamento
ciao eugenio
forse ti può interessare il topic seguente:
https://www.matematicamente.it/forum/un- ... 35248.html
ciao.
https://www.matematicamente.it/forum/un- ... 35248.html
ciao.
Mi sembra chiaro che la prima cifra (quella a sx) abbia un passo di 24 $(n-1)!$
La seconda un passo di 6 $(n-2)!$
La terza 2 $(n-3)!$
La quarta 1 $(n-4)!$
Bisogna solo considerare che trattasi di disposizioni senza ripetizioni, quindi la formuletta deve tenere conto di cio'.
La seconda un passo di 6 $(n-2)!$
La terza 2 $(n-3)!$
La quarta 1 $(n-4)!$
Bisogna solo considerare che trattasi di disposizioni senza ripetizioni, quindi la formuletta deve tenere conto di cio'.
Chiamo x1, x2, x3, x4, x5 le 5 cifre
c1, c2, c3, c4 sono campi di lavoro
posiz è il risultato.
Elaboro x1
c1 = (x1 - 1) * 24
Elaboro x2
se x2 > x1 sottraggo 1 da x2
c2 = (x2 - 1) * 6
Elaboro x3
se x3 > x1 sottraggo 1 da x3
se x3 > x2 sottraggo 1 da x3
c3 = (x3 - 1) * 2
Elaboro x4 e x5
se x5 > x4 ==> c4 = 2
se x5 < x4 ==> c4 = 1
----
posiz = c1 + c2 + c3 +c4
c1, c2, c3, c4 sono campi di lavoro
posiz è il risultato.
Elaboro x1
c1 = (x1 - 1) * 24
Elaboro x2
se x2 > x1 sottraggo 1 da x2
c2 = (x2 - 1) * 6
Elaboro x3
se x3 > x1 sottraggo 1 da x3
se x3 > x2 sottraggo 1 da x3
c3 = (x3 - 1) * 2
Elaboro x4 e x5
se x5 > x4 ==> c4 = 2
se x5 < x4 ==> c4 = 1
----
posiz = c1 + c2 + c3 +c4
Mi piace l'algoritmo, ma la formulazione chiusa mi piace di più 
adaBTTLS ti ringrazio di essere intervenuto
Qul link che mi hai dato riguarda combinazioni di liste aventi lunghezza minore o uguale al numero elementi
Qul link che mi hai dato riguarda combinazioni di liste aventi lunghezza minore o uguale al numero elementi
"Lord K":
Mi piace l'algoritmo, ma la formulazione chiusa mi piace di più
ed un foglio excel che ci metti le cifre e ti da il risultato ?
ehii, qui siamo viziosi.

vi posto la mia soluzione (anche se non la so scrivere in maniera sintetica):
$(a-1)*24+(b-1-{1 " se " b>a})*6+(c-1-{1 " se " c>a}-{1 " se " c>b})*2+(d-1-{1 " se " d>a}-{1 " se " d>b}-{1 " se " d>c})*1+1$
non so se equivale a qualcun'altra già postata. spero che si capisca almeno nelle intenzioni. ciao.
$(a-1)*24+(b-1-{1 " se " b>a})*6+(c-1-{1 " se " c>a}-{1 " se " c>b})*2+(d-1-{1 " se " d>a}-{1 " se " d>b}-{1 " se " d>c})*1+1$
non so se equivale a qualcun'altra già postata. spero che si capisca almeno nelle intenzioni. ciao.
ok Umby
il tuo algortmo funziona alla perfezione.
per verificarlo ho costruito una funzione in linguaggio pyton e per incato mi da la posizione
grazie moltissimo per il tuo aiuto.
ora come devo fare l'inverso,ovvero data la posizione trovarela lista?
saluti eugenio
il tuo algortmo funziona alla perfezione.
per verificarlo ho costruito una funzione in linguaggio pyton e per incato mi da la posizione
grazie moltissimo per il tuo aiuto.
ora come devo fare l'inverso,ovvero data la posizione trovarela lista?
saluti eugenio
"adaBTTLS":
non so se equivale a qualcun'altra già postata. spero che si capisca almeno nelle intenzioni. ciao.
quasi uguale alla mia, almeno i primi 3/4.
Ho semplificato il quarto elemento (x4 <-> x5), per renderla piu' semplice, la tua sintatticamente è perfetta.
"eugenio54":
ok Umby
il tuo algortmo funziona alla perfezione.
e per incato mi da la posizione
ma "incato" sta per "incanto" ?
per la formula al contrario, se si conosce "l'andata" dorebbe essere facile, no ?
Uso una rappresentazione grafica per il contrario:
Esempio: Mi interessa conoscere quale combinazione si trova in posizione 53
Dispongo in una tabella sulla prima colonna i numeri 1,2,3,4,5 (vedi fig. a sinistra)
Sottraggo 1 a 53 = 52
Divido per 24 (Quoziente 2, Resto 4)
Al quoziente 2 corrisponde la terza cifra (0 è il primo, 1 la seconda.....)
Quindi la prima cifra è 3
Dispongo sulla seconda colonna, le cifre rimaste (1,2,4,5)
Divido il resto per 6 (Quoziente 0, Resto 4)
Quindi la seconda cifra è 1
.... continuo cosi, dividendo ancora per 2, e poi per 1
Ottengo la figura a destra ( in rosso le cifre della soluzione) 31524
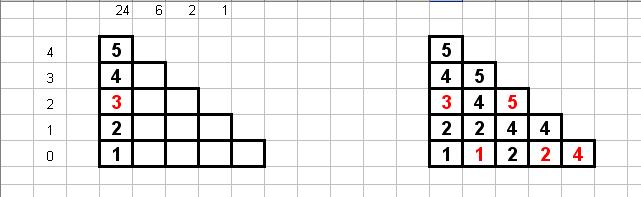
Esempio: Mi interessa conoscere quale combinazione si trova in posizione 53
Dispongo in una tabella sulla prima colonna i numeri 1,2,3,4,5 (vedi fig. a sinistra)
Sottraggo 1 a 53 = 52
Divido per 24 (Quoziente 2, Resto 4)
Al quoziente 2 corrisponde la terza cifra (0 è il primo, 1 la seconda.....)
Quindi la prima cifra è 3
Dispongo sulla seconda colonna, le cifre rimaste (1,2,4,5)
Divido il resto per 6 (Quoziente 0, Resto 4)
Quindi la seconda cifra è 1
.... continuo cosi, dividendo ancora per 2, e poi per 1
Ottengo la figura a destra ( in rosso le cifre della soluzione) 31524

grazie, Umby.
quando ho copiato la formula avevo un po' di fretta... poi ho visto la tua con più calma, anche il foglio di calcolo.
ciao.
quando ho copiato la formula avevo un po' di fretta... poi ho visto la tua con più calma, anche il foglio di calcolo.
ciao.
Grazie Umby, entuasiasmante metodo!
umby volevo dire incanto è saltata la n
anche io avevo seguito il metodo che hai utilizzato per risalire dal posto alla lista ma non decrementavo di 1 il posto e
non ne ho capito il perchè.
grazie sempre per il tuo aiuto.
eugenio
anche io avevo seguito il metodo che hai utilizzato per risalire dal posto alla lista ma non decrementavo di 1 il posto e
non ne ho capito il perchè.
grazie sempre per il tuo aiuto.
eugenio


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo