Tetraedro irregolare

[giammaria2]

Dire con quale procedimento si può calcolare il volume di un tetraedro irregolare, conoscendo i suoi 6 spigoli.

Siamo nella parte del sito dedicato alla superiori, quindi sono esclusi gli argomenti universitari, fra cui analitica e trigonometria tridimensionali. Ribadisco che non sono richiesti i calcoli, ma solo il procedimento, esposto in modo un po' dettagliato.
Ho preso spunto da questo problema; consiglio di far riferimento alla sua figura.

[Sascia63]

Non sto riportando la dimostrazione in quanto ci sto ancora lavorando ma conoscendo gli spigoli esiste già il determinante di Cayley-Menger:
http://mathworld.wolfram.com/Cayley-Men ... inant.html

[giammaria2]

Avevo escluso gli argomento universitari e direi che il tuo inizio di soluzione non rientra nel programma delle superiori.

[Erasmus_First]

"giammaria":[...] Siamo nella parte del sito dedicato alla superiori, quindi sono esclusi gli argomenti universitari, fra cui analitica e trigonometria tridimensionali. Ribadisco che non sono richiesti i calcoli, ma solo il procedimento, esposto in modo un po' dettagliato.
Ho preso spunto da questo problema; consiglio di far riferimento alla sua figura.

@ giammaria [ot]Ho messo quel problemna in "pensare un po' di più" perché anche per trovare solamente il volume occorre avere qualche informazione con cui ricavare il seno di un angolo diedro. Se no come si può trovare la distanza di un vertice dal piano della faccia opposta?
Credo che non si possa!
Certo: ricavare il coseno di un angolo diedro tramite i coseni degli angoli piani delle tre facce di un triedero del quale l'angolo diedro in questione è uno dei tre angoli diedri del triedro è abbastanza facile (e serve l'uso della sola trigonometria piana). Ma questo risultato è appunto il "1° teorema del coseno" della Trigonometria sferica. Quel mio post voleva essere un po' polemico! Denunciare cioè quella che secondo me è una lacuna: l'assenza di un minimo di trigonometria sferica (che reputo facile e molto formativa) sia nelle cosiddette "superiori" che nel biennio di "scienze" e persino nel primo biennio di Matematica – sempre secondo i miei ricordi, che però sono ormai di 55 - 60 anni fa.
A|llora: perché tu non hai risposto a quel mio quiz?
Ciao ciao.
Erasmus[/ot]
_________

[giammaria2]

Si può rispondere alla mia domanda usando, di tridimensionale, solo la formula per il volume di una piramide ed il teorema delle tre perpendicolari: argomenti che vengono fatti nelle superiori. O almeno, che dovrebbero essere fatti: nelle superiori italiane, la geometria solida spesso è la Cenerentola della matematica.
Non ho risposto al tuo quiz per molti motivi: uno è che non l'avevo visto, non avendo l'abitudine di leggere quella parte di forum, ed un altro è che ho pensato che certo c'erano soluzioni universitarie e quindi migliori della mia (all'università non ho studiato geometria solida). Inoltre ne ho poi trovato una soluzione che richiedeva la conoscenza del volume; il mio attuale quiz chiede appunto quello. Preciso che in questo momento non ricordo quale fosse la soluzione di cui ho appena parlato.

[axpgn]

Forse una soluzione ce l'avrei ... forse

Il volume lo calcolo come per le piramidi: area di base per altezza diviso tre (giusto? mi pare ... )
L'area di base la trovo con Erone.
Per l'altezza, prima trove le tre altezze relative alle facce ed il punto dove cadono sui lati di base, usando tre sistemi da due equazioni usando Pitagora.
Dal piede dell'altezza del tetraedro partono tre segmenti verso i tre vertici di base e tre verso i piedi delle tre altezze, formando sei triangoli rettangoli; sei incognite e un sistema di sei equazioni, trovato uno dei segmenti, si calcola l'altezza con Pitagora.
Isn't it?

Cordialmente, Alex

[giammaria2]

@ axpgn
Forse è giusto, ma ...

Parli di sistemi, ma per i primi non mi è chiaro cosa metti a sistema; in quella parte, io non ho usato sistemi. Per il sistema finale, ho l'impressione che alcune equazioni siano combinazioni lineari delle altre; inoltre sarebbe meglio evitare un sistema di sei equazioni.

[axpgn]

Ho "condensato" il più possibile data la "non voglia" di scrivere in questo periodo ...

Con i "primi" sistemi volevo dire questo: per esempio, prendi il triangolo $ABD$ e traccia l'altezza $DH_c$, allora avrai ${(d^2=(DH_c)^2+(AH_c)^2),(e^2=(DH_c)^2+(c-AH_c)^2):}$ che si risolve in un attimo.
Non saprei se qualcuna delle sei equazioni dipende dalle altre, ma penso di no ma concordo sul fatto che siano tante

Nel thread originale di Erasmus si chiedeva di calcolare il raggio della sfera circoscritta; io l'ho fatto ma in un altro thread (che non ricordo) perché richiesto da Erasmus (che non ha ancora confermato se il mio risultato è corretto o meno).
Per calcolarlo ho trovato le coordinate dei quattro vertici: due immediati, il terzo quasi (intersecando due circonferenze), il quarto intersecando tre sfere, ed infine intersecando quattro sfere di raggio incognito ma uguale per tutte.
Tranne l'ultimo passaggio, questa procedura mi permette di trovare l'altezza della piramide ... però qualcosa mi dice che non ti vada bene ...

Cordialmente, Alex

[giammaria2]

@axpgn

Sono d'accordo per i primi sistemi. Io avevo ragionato così: con Erone calcolo l'area S di ABD e ne deduco $DH_c=(2S)/c$; $AH_c$ è poi calcolato con Pitagora.

Per l'ultimo sistema, dovrei sapere esattamente quali sono le tue equazioni; mi pare che tu ragioni sul piano di base ed allora, detto P il piede dell'altezza del tetraedro, direi che le uniche che riguardano il vertice A sono
$bar(AH_c)^2+bar(PH_c)^2=bar(AP)^2" "$ e $" "bar(AH_b)^2+bar(PH_b)^2=bar(AP)^2$
Da una di esse ricavo l'incognita $bar(AP)$ e la sostituisco nell'altra; indicando con $x,y$ le due incognite rimanenti ($x=bar(PH_c);y=bar(PH_b)$), ho l'equazione
$bar(AH_c)^2+x^2=bar(AH_b)^2+y^2$
scrivibile come $x^2-y^2=a_1$, essendo $a_1$ un numero noto.
Per gli altri vertici ottengo equazioni dello stesso tipo. Osservando i primi membri, noto che quello della terza equazione è combinazione lineare degli altri due, e questo basta per dire che il sistema è indeterminato o impossibile. La geometria del problema dice però che con dati ragionevoli c'è una ed una sola soluzione; se ne conclude che il nostro sistema è indeterminato e che per la soluzione ci manca un'equazione.

[axpgn]

@giammaria

Se lo dici tu, mi fido; non ho voglia di fare conti ...
È che volendo usare solo i lati e niente angoli, c'è sempre un incognita di troppo

Però, forse ... se il piede dell'altezza della piramide coincide con l'incentro della base allora forse ho risolto; dai dati che ho posso trovare le coordinate dell'incentro e con queste (e il resto) l'altezza ... che ne dici?

EDIT:

Che ne pensi della "procedura" con cui ho trovato il raggio della "sfera di Erasmus" ?

Cordialmente, Alex

[giammaria2]

@ axpgn

Se lo dici tu, mi fido; non ho voglia di fare conti ...

Ti ringrazio della fiducia, ma non so di che conti parli: io non ne ho fatti ed ho solo indicato un procedimento.
O forse ti riferisci alla mia affermazione sulle combinazioni lineari: intendevo solo dire che nel sistema
${(x^2-y^2=a_1),(y^2-z^2=a_2), (z^2-x^2=a_3):}$
il primo membro della terza equazione è la somma, cambiata di segno, degli altri primi due.

È che volendo usare solo i lati e niente angoli...

Ma puoi tranquillamente usare gli angoli nel piano, basta che tu ricordi che non sono fra i dati e che devi limitarti ad argomenti preuniversitari.

se il piede dell'altezza della piramide coincide con l'incentro della base...

No: gli spigoli possono avere qualsiasi lunghezza ragionevole (cioè devono soddisfare alle diseguaglianze triangolari) e quindi il piede dell'altezza può essere in qualsiasi punto della base.

Che ne pensi della "procedura" con cui ho trovato il raggio della "sfera di Erasmus" ?

Non l'ho ancora letta, ma è probabile che sia all'altezza dei tuoi soliti interventi, e cioè ottima.

[axpgn]

@giammaria

"giammaria":... il primo membro della terza equazione è la somma, cambiata di segno, degli altri primi due. ...

Sì, avevo capito che intendevi questo ma non avevo voglia di verificare se fosse proprio così

"giammaria":Ma puoi tranquillamente usare gli angoli nel piano, ...

Ma non voglio usarli ... tra l'altro questo concetto di "soli argomenti preuniversitari" è molto scivoloso (vedi Erasmus); penso sia difficile stabilire il confine (che varia nel tempo, dal tipo di scuola ed anche da istituto ad istituto)

"giammaria":... e quindi il piede dell'altezza può essere in qualsiasi punto della base.

E questa è una fregatura ... ... d'altronde bastava m'immaginassi una faccia della piramide molto ripida con l'altro spigolo lungo lungo per far cadere il piede della piramide quasi sul bordo ...

Però adesso mi è venuta un'altra idea ... io posso determinare $H_c, H_b, H_a$ ed anche le rette passanti per essi perpendicolari ai lati; queste si incontrano certamente in $P$ (piede dell'altezza della piramide) perché se io guardo il tetraedro "da sopra" vedo che le altezze relative ai lati "collassano" su tre segmenti appartenenti alle rette suddette, che si incontrano in $P$ proiezione di $D$.
A 'sto punto basta fare il sistema tra loro (ma ne bastano due, credo) e trovo le coordinate di $P$ e quindi l'altezza e quindi il volume ... it's ok?

"giammaria":... e cioè ottima.

Adesso sei tu che hai troppa fiducia ...

Cordialmente, Alex

[orsoulx]

Proposta di soluzione, per la serie 'a basso livello tutto quel che si può fare con la trigonometria si può fare senza', convincente (a mio avviso), che richiede minime conoscenze di algebra ed i teoremi di Pitagora a 2 e 3 dimensioni (implicitamente viene utilizzato il teorema delle tre perpendicolari, ma mica lo diciamo).

Con riferimento al disegno di Erasmus ed alle relative misure. Sia $ f $ lo spigolo di maggior lunghezza $ f, a, c $ e $ a,b,d $ gli spigoli delle due facce con $ a $ in comune.
Le altezze $ h $ e $ k $ di queste due facce rispetto ad $ f $ cadono su questo segmento ed indicando con $ m $ ed $ n $ le rispettive distanze dei loro piedi da C abbiamo, con il solo TP:
$ a^2-m^2=c^2-(f-m)^2 $, equazione che si riduce al primo grado con cui si trova $ m = (f^2+a^2-c^2)/(2f) $ da cui col TP otteniamo $ h $.
Analogamente per l'altra faccia troviamo $ n $ e $ k $. Calcoliamo ancora $ s= | m-n | $.
Pensando le due facce appoggiate sul piano di base del tetraedro, facciamo ruotare la seconda fino a quando la distanza $ AB $ diventa uguale a $ e=43 $. Durante il movimento $ B $ descrive un arco di circonferenza in un piano perpendicolare a $ DC $ e la proiezione $ A' $ di $ A $ su questo piano disterà da B ( quando questo si è sistemato per bene) di $ l= sqrt(e^2-s^2) $.
Il triangolo di spigoli $ h,k,l $ si 'risolve' come le prime due facce, per trovare (era ora!), l'altezza del tetraedro.
Tutto come vuole Erasmus e giocando a non parlare mai di angoli.

Ciao

[Erasmus_First]

"giammaria":Si può rispondere alla mia domanda usando, di tridimensionale, solo la formula per il volume di una piramide ed il teorema delle tre perpendicolar [...]

[ot]@ giammaria
Per la stima che ho di te dovrei crederti sulla parola!
Ma io (che conosco ... – ed ho anche insegnato! – il "Teorema delle 3 perpendicolari) non vedo come possa essere sfruttato per trovare la distanza di un vertice dal piano della faccia opposta.
Per favore ... esponi tu la procedura che hai trovato per calcolare l'altezza della piramide conoscendo le lunghezze dei lati della base e quelle degli spigoli delle tre facce "laterali".[/ot]
Suppongo che, nella sostanza, la "tua" procedura per calcolare l'altezza della piramide, contenga gli stessi passaggi che servono per calcolare il coseno di un angolo diedro.
[Insomma: la distanza del piede dell'altezza da un lato della base è il prodotto dell'altezza di una faccia laterale rispetto allo spigolo comune alla faccia-base per il coseno dell'angolo diedro con questo spigolo (cioè "faccia_base –faccia-laterale").
Ho visto che è intervenuto anche orsoulx, ma non sono sicuro di aver raccolto tutti i suoi passaggi. Adesso mi viene in mente una procedura come chiede giammaria.
Siano [b, d, f] e [c, d, e] le terne di spigoli di due facce laterali ( e [a, b, c] la terna di spigoli della faccia assunta come base). Le proiezioni ortogonali dello spigolo comune d sugli spigoli b e c della base siano rispettivamente
$m = (b^2 + d^2 – f^2)/(2b)$;
$n = (c^2 + d^2 – e^2)/(2c)$.
Queste proiezioni sono due lati di un quadrilatero i cui altri due lati sono i segmenti "distanze" del piede dell'altezza (della piramide) dai due spigoli b e c. Posso allora (con Carnot) calcolare la lunghezza d'una diagonale di questo quadrilatero: quella diversa da quella che ha per estremi l'estremo comune degli spigoli b, c e d ed il piede dell'altezza sulla faccia_base.Posso allora calcolare gli angoli del triangolo costituito da questa diagonale (nota) e dalle distanze (incognite) dei suoi estremi dal piede dell'altezza. Finalmente, col teorema dei "seni" posso trovare una di queste distanze (per esempio quella dallo spigolo c) , Calcolata allora l'altezza della faccia rispetto a quello spigolo della base (che nell'esempio era c) , trovo con Pitagora l'altezza della piramide.
[Mi sa che la "procedura" di orsoulx è proprio questa. Gli chiedo scusa: ma non me la sento di andarmela a rileggere con attenzione per controllare ... perché ormai sono fuso e riesco a malapena a i miei "ragionamenti"]
-------------
Oggi pomeriggio ho lavorato a comporre due immagini con figure e testo per mostrare la via più diretta per il calcolo del volume. Questa fa uso di un facile teorema di trigonometria sferica del quale metto più sotto la dimostrazione.
Ecco qua:

––––––
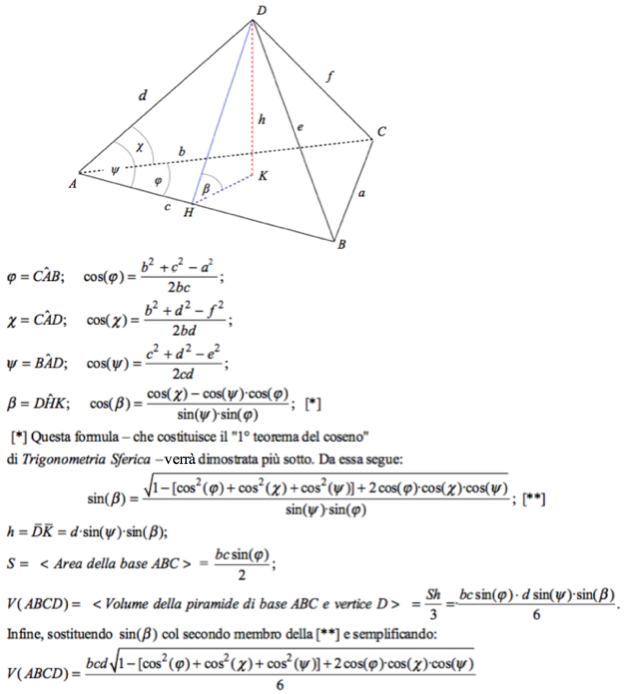
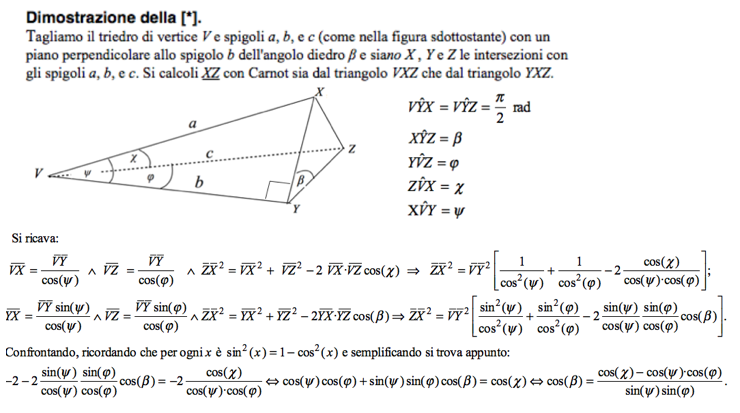
Ieri, con pazienza certosina, ho sostituito le funzioni "coseno" che stanno nell'espressione del volume del tetraedro con le rispettive funzioni razionali (degli spigoli) ottenendo l'espressione che vedete nella figura seguente (relativa ad un tetraedro con gli spigoli disposti come nella prima figura di questo mio intervento).

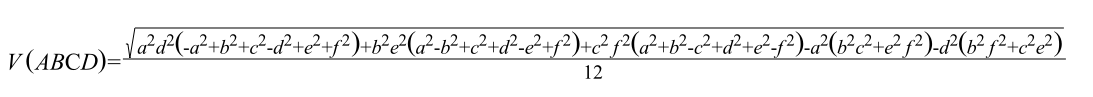
Accidenti non si vede tutta! Occorre aprirla fuori del forum. Allora metto il link apposito:
––> Formula del volume del tetraedro irregolare
Sotto radice c'è un polinomio con ben 22 termini. Ma è facilissimo ricordare come è fatto!
Bisogna prima vedere quali sono le tre coppie di spigoli opposti (cioè "non complanari") e quali sono le quattro terne di spigoli che sono i lati delle quattro facce.
Nel disegno qui sopra si nota che le coppie di spigoli opposti sono
[a, d]; [b, e]; [c, f]
e che le terne lati delle facce sono
[a, b, c]; [a, e, f]; [b, d, f ]; [c, d, e].
Allora l'espressione sotto radice si costruisce come segue:
a) Si fa il prodotto dei quadrati di due spigoli opposti e lo si moltiplica per la somma dei quadrati di tutti i sei spigoli ma poi si cambia il segno da "+" a "–" dei due addendi che sono i quadrati degli stessi spigoli opposti.
Dunque, per la coppia di spigoli opposti [a, d] abbiamo:
$a^2d^2(–a^2 + b^2 + c^2 – d^2 + e^2 + f^2)$·
Per la coppia di spigoli opposti [b, e] abbiamo:
$b^2e^2(a^2 - b^2 + c^2 +d^2 –e^2 + f^2)$.
Per la coppia di spigoli opposti [c, f] abbiamo
$c^2f^2(a^2 + b^2 – c^2 + d^2 + e^2 –f^2)$.
Naturalmente si fa la somma di queste tre espressioni (arrivando fin qua a 18 termini).
b) Alla precedente somma si sottraggono i quattro prodotti dei quadrati dei lati delle 4 facce; si aggiunge cioè:
$–(a^2b^2c^2 + a^2e^2f^2+b^2d^2f^2+c^2d^2e^2)$.
c) Si fa la radice quadrata di questa sfilza di 22 termini (12 a coefficiente 1 e 10 a coefficiente –1) e la si divide per 12.
________


________________________________
P.S. (Editando)
Ho corretto un errore (di ortografia – c'era un "verà" con una sola "r" al posto di "verrà" – e così ho dovuto rifare l'hosting e inserire l'immagine nuova.
Ciao ciao.

[giammaria2]

Non conoscevo le formule per $m,n$ indicate da Erasmus_First e quindi non le ho usate. Do la mia soluzione, lasciandola in chiaro dato che è ormai passato abbastanza tempo.
Indico con $K$ la proiezione di $D$ sul piano ABC e con $H_b,H_c$ le proiezioni di K sui lati AC, AB; per il teorema delle tre perpendicolari, $H_b,H_c$ sono i piedi degli apotemi delle loro facce laterali.
Con Erone calcolo l'area S di ABD e ne deduco $DH_c=(2S)/c$; per Pitagora ho $AH_c=sqrt(d^2-DH_c^2)$.
Nello stesso modo calcolo $AH_b$ e poi sposto l'attenzione sul piano di base, in cui l'angolo $B hatAC=alpha$ è calcolabile con Carnot. Posto $x=K hatAH_c; y=K hatAH_b$, noto che si ha

$AK cosx=AH_c" "$ e $" "AK cosy=AH_b$

ed eliminando l'incognita AK ne deduco $AH_c cosy=AH_bcosx$
Metto questa equazione a sistema con $x+y=alpha$ e risolvo facilmente il sistema, ricavando le tangenti dei due angoli.
Posso ora concludere in vari modi; uno di essi è calcolare

$KH_c=AH_c tanx$

$h=DK=DH_c^2-KH_c^2$

$V=1/3 S(ABC)*h$ (avendo calcolato $S(ABC)$ con Erone)

NOTA. Ho limitato l'attenzione al solo caso generale; ad esempio, se $x$ fosse retto non potrei calcolarne la tangente. Oppure, se ci fosse qualche angolo ottuso, è possible che qualche punto vada modificato (forse basterebbe pensare a valori negativi, ma forse no). Ma ho preferito non dilungarmi troppo.

[orsoulx]

"Erasmus_First":Mi sa che la "procedura" di orsoulx è proprio questa

Improbabile, visto che non utilizzo alcun angolo che non sia retto.
Ciao
Complimenti per la pazienza con cui hai ricavato l'espressione esatta del volume in funzione dei sei spigoli.
Il determinante proposto da Sciascia63 ne è più compatta ma, come già segnalato da giammaria la discussione abita in "scervelliamoci un po'".

[Erasmus_First]

@ giammaria
Ho sviluppato dettagliatamente il percorso che avevo segnalato in precedenza, cioè di sfrattare le informazioni relative al piede dell'altezza ,...e ne ho fatto un "paper" di una pagina che metto come immagine png qui sotto

Ciao ciao
Erasmus
-------
P.S (Editando)
Ho cambiato l'immagine (perché aveva un errore, (un "phi" al posto di un "theta"). Qualla attuale è identica alla precedente tranne la correzione di un solo carattere greco ( da "phi" a "theta")
______

[giammaria2]

Complimenti!

[40rob]

Visto che ne sapete molto su questi argomenti, sapete se esiste qualche analogia tra 2 dimensioni e 3 dimensioni per cui fissate le 4 aree delle facce di un tetraedro qualsiasi (senza avere alcuna informazione sugli spigoli) rimane fissato il volume? (sempre se esiste un tetraedro con queste quattro aree fissate).
Esiste una qualche formula abbastanza semplice simile a quella di Erone in cui si inseriscono al posto delle lunghezze dei lati le aree delle 4 facce e questa formula magari diventa negativa sotto qualche radice pari quando il tetraedro in questione non esiste (con i quattro valori) mentre altrimenti tira fuori il volume?
Insomma una formula che funziona proprio come quella di Erone che diventa negativa sotto radice quando i tre lati non riescono a formare un triangolo. Sempre sotto l'ipotesi che esiste questa relazione univoca tra valori delle aree delle facce e volume. Io non riesco a capirlo se esiste.
Può essere che non c'è proprio ovviamente, fissate 4 aree delle facce magari esistono più tetraedri con volumi distinti.
Ho cercato un po' in rete ma non ho trovato molte informazioni a riguardo, c'è solo la formula che lega gli spigoli al volume.

[40rob]

Risolto... Non si può fare, stesse aree delle facce possono produrre volumi diversi.

[orsoulx]

"bub":Risolto...

Hai posto un bel problema e non mi pare il caso di condannarlo a morte in questo modo.
Se l'area della faccia più grande è minore della somma di quelle delle restanti, mi pare, esistano tetraedri, con facce delle misure assegnate, di diverso volume.
La formula che cercavi non si può trovare, ma ci possiamo porre problemi, a mio avviso, interessanti:
- è possibile trovare una procedura per costruire uno o più tetraedri con facce di quelle misure?
. qual è il minimo/massimo volume di un tetraedro siffatto?
Credo di esser in grado di rispondere alla prima domanda, ma non alla seconda.
Ciao