Problema
ragazzi voglio sottoporvi un problema ...
conoscendo soltanto i dati relativi alla circonferenza (una qualsiasi ipotetica circonferenza) è possibile calcolare il seguente quadrato? ovvero avente un lato sul diametro con il punto medio al centro della circonferenza e spigoli superiori tangenti ad essa?
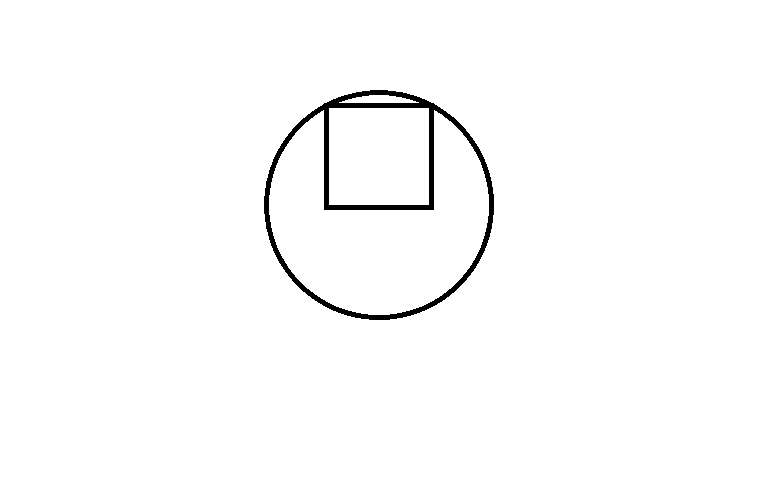
conoscendo soltanto i dati relativi alla circonferenza (una qualsiasi ipotetica circonferenza) è possibile calcolare il seguente quadrato? ovvero avente un lato sul diametro con il punto medio al centro della circonferenza e spigoli superiori tangenti ad essa?

Risposte
Certo. Congiungi il centro della circonferenza con uno dei vertici sulla circonferenza. Ottieni un triangolo rettangolo che ha il raggio come ipotenusa e i cateti che sono uno il lato del quadrato e l'altro la sua metà.
Certo! ...questo conoscendo la posizione esatta dei vertici ...ma io non la conosco...ovvero ho come unico dato la circonferenza ....
facciamo conto di voler avere in quella posizione un quadrato 20x 20 il mio unico dato però è una circonferenza di raggio 22.3607...(che è proprio la circonferenza per un quadrato 20 x 20)questo è un esempio ...ma se volessi proprio un quadrato perfetto in quella posizione partendo da una generica circonferenza come faccio? credo che tutte le possibili circonferenze possano constare di quel particolare quadrato in quella posizione
la domanda rimane insoluta aspetto vostre risposte


facciamo conto di voler avere in quella posizione un quadrato 20x 20 il mio unico dato però è una circonferenza di raggio 22.3607...(che è proprio la circonferenza per un quadrato 20 x 20)questo è un esempio ...ma se volessi proprio un quadrato perfetto in quella posizione partendo da una generica circonferenza come faccio? credo che tutte le possibili circonferenze possano constare di quel particolare quadrato in quella posizione
la domanda rimane insoluta aspetto vostre risposte
Non è che abbia capito bene cosa tu voglia esattamente ma data qualsiasi circonferenza per ottenere i due punti che costituiscono gli estremi del lato del quadrato che toccano la circonferenza ti basta tracciare due raggi formanti un angolo di 53 gradi e qualcosina …
Cordialmente, Alex
Cordialmente, Alex
"axpgn":
Non è che abbia capito bene cosa tu voglia esattamente ma data qualsiasi circonferenza per ottenere i due punti che costituiscono gli estremi del lato del quadrato che toccano la circonferenza ti basta tracciare due raggi formanti un angolo di 53 gradi e qualcosina …
Cordialmente, Alex
No comunque non mi trovo ... ho provato partendo dal quadrato e disegnando la circonferenza anche se é quello che non voglio io poiché voglio partire dalla circonferenza per trovarmi quel particolare quadrato...in ogni caso L angolo é di 63 gradi ma comunque L angolo varia a seconda della circonferenza secondo me va fatto qualche calcolo più approfondito ...penso al p greco o qualche calcolo in trigo...
Va be chiunque mi può aiutare resto in ascolto
"miksons":
... un lato sul diametro con il punto medio al centro della circonferenza ...
sufficit per calcolare il lato del quadrato in funzione del raggio della circonferenza, col teorema di Pitagora.
Cos'altro vuoi trovare ?
@miksons
Come detto da veciorik, da @melia e da me, i dati sono sufficienti.
Il rapporto tra lato del quadrato è circonferenza è FISSO e vale $l/r=2/sqrt(5)$.
L'angolo non è quello da te detto anche perché altrimenti sarebbero più lunghi i lati del raggio.
Come detto da veciorik, da @melia e da me, i dati sono sufficienti.
Il rapporto tra lato del quadrato è circonferenza è FISSO e vale $l/r=2/sqrt(5)$.
L'angolo non è quello da te detto anche perché altrimenti sarebbero più lunghi i lati del raggio.
@ veciorik
si ma ciò se conoscessi la misura del lato ma come ho detto io non conosco la misura del lato ... quello che voglio dire e che in quel punto ovvero al centro della circonferenza avrò il punto medio del mio quadrato di cui non conosco il lato! quindi il teorema di pitagora lo potrei applicare se avessi come dato la misura del lato ma ho come unico dato la circonferenza ....
@ axpgn
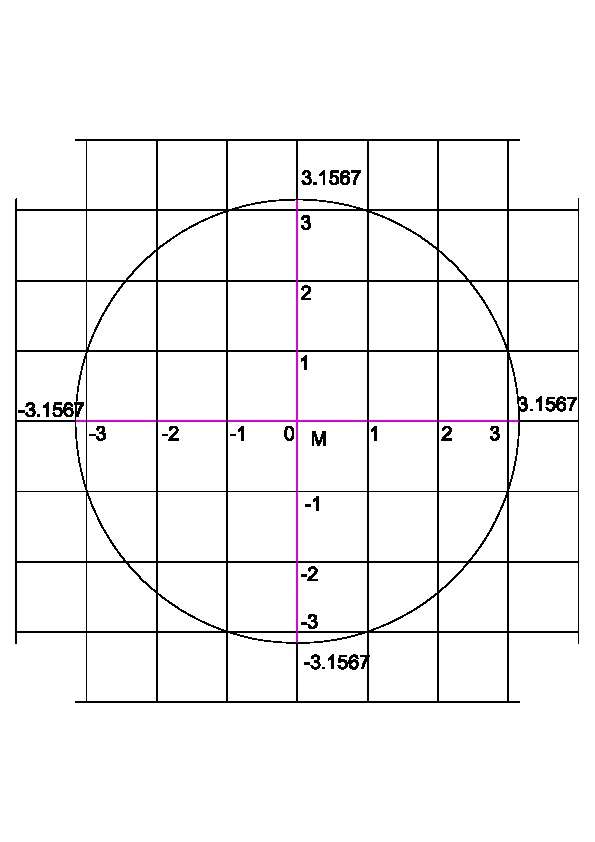
lo hai risolto ...ma continuo a non capire scusa la mia ignoranza ma non ho ben capito ...questa è una formula applicabile ad una qualsiasi circonferenza ? nel senso puta caso io ho una circonferenza di diametro 3.1567 come lo risolveresti? aiutami a capire...
si ma ciò se conoscessi la misura del lato ma come ho detto io non conosco la misura del lato ... quello che voglio dire e che in quel punto ovvero al centro della circonferenza avrò il punto medio del mio quadrato di cui non conosco il lato! quindi il teorema di pitagora lo potrei applicare se avessi come dato la misura del lato ma ho come unico dato la circonferenza ....
@ axpgn
lo hai risolto ...ma continuo a non capire scusa la mia ignoranza ma non ho ben capito ...questa è una formula applicabile ad una qualsiasi circonferenza ? nel senso puta caso io ho una circonferenza di diametro 3.1567 come lo risolveresti? aiutami a capire...

Ipotesi: hai una circonferenza di raggio $r$ qualsiasi; hai un lato $l$ del quadrato posizionato su un diametro del cerchio e il punto medio di questo lato coincide col centro della circonferenza; gli estremi del lato del quadrato opposto a quello che sta sul diametro stanno sulla circonferenza.
Ci siamo fino qui? Ok
Chiamiamo $O$ il centro della circonferenza, $A$ e $B$ i vertici del quadrato che stanno sulla circonferenza e $M$ il punto medio di $AB$
Congiungo $O$ con $A$ e e $O$ con $B$: questi sono raggi e quindi $OA=OB=r$
Congiungo $O$ con $M$ e quindi $OM=l$
Il triangolo $AOM$ è rettangolo in $M$ (così come $BOM$)
Applico il teorema di Pitagora: $(AO)^2=(OM)^2+(AM)^2$ ovvero, sostituendo, $r^2=l^2+(l/2)^2$ da cui $r^2=5/4l^2$ e ne consegue che il rapporto tra lato del quadrato e raggio della circonferenza è fisso e vale $l/r=2/sqrt(5)$
Tale valore è anche quello della tangente dell'angolo al centro $AOM$.
Come puoi vedere non ci sono valori puntuali di raggi e lati
Ci siamo fino qui? Ok
Chiamiamo $O$ il centro della circonferenza, $A$ e $B$ i vertici del quadrato che stanno sulla circonferenza e $M$ il punto medio di $AB$
Congiungo $O$ con $A$ e e $O$ con $B$: questi sono raggi e quindi $OA=OB=r$
Congiungo $O$ con $M$ e quindi $OM=l$
Il triangolo $AOM$ è rettangolo in $M$ (così come $BOM$)
Applico il teorema di Pitagora: $(AO)^2=(OM)^2+(AM)^2$ ovvero, sostituendo, $r^2=l^2+(l/2)^2$ da cui $r^2=5/4l^2$ e ne consegue che il rapporto tra lato del quadrato e raggio della circonferenza è fisso e vale $l/r=2/sqrt(5)$
Tale valore è anche quello della tangente dell'angolo al centro $AOM$.
Come puoi vedere non ci sono valori puntuali di raggi e lati
Grazie, questo era quello che avevo scritto nel primo mio intervento e che, ovviamente, miksons non aveva capito.
Grazie a tutti ragazzi ! ho capito! 



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo