Calcolo della lunghezza di una corda di un triangolo

[Erasmus_First]

Sia ABC un triangolo acutangolo e siano note le lunghezze dei suoi lati, cioè:
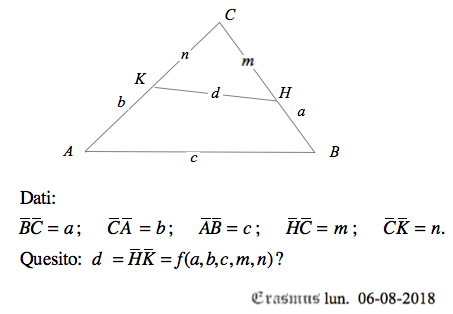
BC = a; CA = b; AB = c.
Sia H il punto interno al lato BC distante m da C e sia K il punto interno al lato CA distate n da C.
Detta d = HK la distanza tra H e K, calcolare d [in funzione di a, b, c, m ed n] IGNORANDO LA TRIGONOMETRIA (cioè senza usare le funzioni circolari).
________



P.S. (Editando)

$I$llustrazione postuma!

[giammaria2]

Bé, c'è il teorema di Pitagora generalizzato: "In un triangolo il quadrato del lato opposto ad un angolo acuto è uguale alla somma dei quadrati degli altri due, diminuita del doppio prodotto di un lato per la proiezione dell'altro su di esso". E' un modo di barare perché in realtà è una forma mascherata (neanche tanto) del teorema di Carnot; la trigonometria non viene però nominata.
Con questo, basta proiettare B ed H su AC e poi usare la similitudine.

[axpgn]

Sul momento a me viene un procedimento molto lungo ma tutto sommato, semplice ...

Si trova l'altezza da $C$ (usando Pitagora sui due triangoli rettangoli formati da questa)
Si tracciano in $H$ e $K$ le parallele alla base $AB$ e sfruttando la proporzionalità delle similitudini la lunghezza delle stesse ed anche delle altezze dei vari triangolini.
Si calcolano quindi le aree dei triangolini che contengono $HK$ e usando Erone al contrario si determina la lunghezza di $HK$

Cordialmente, Alex

[sandroroma]

$\overline{HK}=\sqrt{m^2+n^2-2mn\sqrt{1-(\frac{2S}{ab})^2}}$
dove $S $ è l'area del triangolo.

[axpgn]

Spoiler, please

[Erasmus_First]

"sandroroma":

$\overline{HK}=\sqrt{m^2+n^2-2mn\sqrt{1-(\frac{2S}{ab})^2}}$
dove $S $ è l'area del triangolo.

Però:
a) Come hai fatto?
[Penso che hai fatto come ho fatto anch'io, (cioè tracciando da H e da C le perpendicolari ad AB e sfruttando poi la similitudine tra due triangoli rettangoli)].
b) Si chiedeva di dare l'espressione di d = HK "in funzione di a, b, c e d" (cioè dei dati).
c) Se invece di $((2S)/(ab))^2$ metti $((4S)/(2ab))^2$ e di $16S^2$ metti l'espressione in a, b e c vedi subito che $(4a^2b^2–16S^2)/(4a^2b^2)$ è un quadrato perfetto.

[D'altra parte, se non fosse vietato l'uso della trigonometria si avrebbe subito:
$cos(γ)=(a^2 + b^2 – c^2)/(2ab)$;
$d^2 = m^2 + n^2 –2mn·cos(γ)= (ab(m^2+n^2) – mn(a^2+b^2 - c^2))/(ab)$.
Voglio dire: si può sapere a cosa bisogna arrivare ancor prima di iniziare il percorso senza trigonometria].
_________


[ot]P.S.
@ Alex e Giammaria
Vedo solo ora i vostri interventi.
Infatti avevo scritto la risposta a sandroroma (ma dimenticando poi di cliccare"Invia"! ) ieri sera quando non c'erano ancora i vostri interventi.
Ciao, ciao.[/ot]

[Erasmus_First]

"Error in procedendo!" [C'ra un doppione del messaggio di sopra! Credo che non mi sia possibile cancellarlo perché non è l'ultimo inrvento. Ma forse è possibile al moderatore.
Please, @melia: erase it to me! Thank you for your attention.

[axpgn]

"Erasmus_First":@ Alex e Giammaria
Vedo solo ora i vostri interventi.
Infatti avevo scritto la risposta a sandroroma (ma dimenticando poi di cliccare"Invia"! ) ieri sera quando non c'erano ancora i vostri interventi.
Ciao, ciao.

Quindi sei anche un veggente dato che i nostri interventi sono precedenti quello di sandroroma

Cordialmente, Alex

[Erasmus_First]

"axpgn":Quindi sei anche un veggente dato che i nostri interventi sono precedenti quello di sandroroma

No. Certamente sono – da circa 13 anni, a seguito d'un distacco di retina – un "ipovedente"!
[E, ormai da qualche anno, anche un "pasticcione"]
[Per esempio, vedo solo adesso un "doppione" del messaggio che permette ad Alex di "turlupinarmi" ... ( "cordialmente", of course) .
Ma il "doppione" lo andrò subito a cancellare]

Può darsi che davvero voi abbiate risposto prima di sandroroma ... ma io sarei pronto a giurare che la sera che ho risposto [o meglio: credevo di aver risposto] a sandroroma il suo intervento era l'unico (ed il primo dopo parecchie visite senza interventi).
Essendo "ipovedente" e "pasticcione"... non sono sicurissimo di niente: ma potrebbe succedere (per esempio) che uno, volendo correggere la sua risposta e non vedendo ancora risposte dopo la sua, cancella il proprio messaggio e lo ripete corretto ... ma mentre fa questo arrivate voi (intrusi! ) a rubargli la primogenitura!
_______