Sessione ordinaria 1990

[smak7]

Avrei bisogno di una mano per la risoluzione della sessione ordinaria della maturità scientifica del 1990.
Questo è il testo del primo problema:

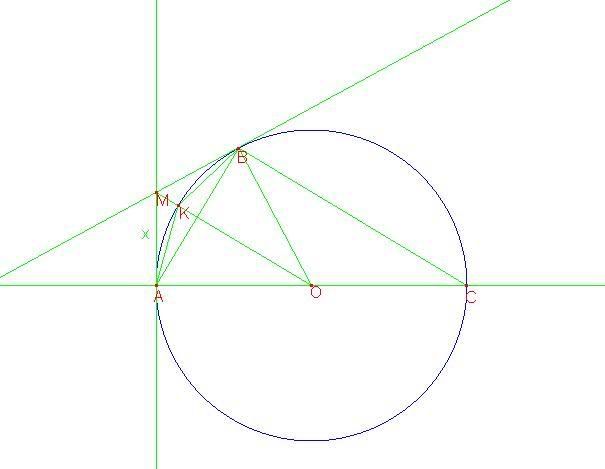
Data la circonferenza di diametro AC=2r e centro O, tracciare la semiretta uscente da A, perpendicolare ad AC e giacente rispetto ad AC dalla stessa parte della semicirconferenza. detto M un punto generico di tale semiretta, indicare con x la distanza di M da A. Da M staccare l'ulteriore tangente in B alla semicirconferenza. Detta K l'intersezione della semicirconferenza con il segmento OM, determinare l'area y del quadrilatero ACBK in funzione di x.

[Sk_Anonymous]

Sia N l'intersezione di OM con AB (non indicata in figura).
Comincio col ricordare che ,in un triangolo rettangolo,l'altezza
relativa all'ipotenusa e' uguale al prodotto dei cateti diviso l'ipotenusa.
Inoltre BC ed ON sono paralleli ,essendo entrambi perpendicolari ad AB.
Pertanto,poiche e' AC=2AO, e' pure BC=2ON
Cio' premesso si ha :
$OM=sqrt(AO^2+AM^2)=sqrt(r^2+x^2)$
$AN=(AO*AM)/(OM)=(rx)/(sqrt(r^2+x^2)$
$ON=(AO^2)/(OM)=(r^2)/(sqrt(r^2+x^2)$ (1° teorema di Euclide)
$S(ABC)=1/2AB*BC=AN*2ON=2AN*ON$
$S(ABK)=1/2AB*KN=AN*(OK-ON)=AN*OK-AN*ON$
Ne segue che:
$S(ACBK)=S(ABC)+S(ABK)=AN*OK+AN*ON=AN*(OK+ON)$
E sostituendo i valori trovati:
$S(ACBK)=(rx)/(sqrt(r^2+x^2))*(r+(r^2)/(sqrt(r^2+x^2)))$
E alla fine:
$S(ACBK)=(r^2x)/((r^2+x^2))*(r+sqrt(r^2+x^2))$
karl

[smak7]

ti ringrazio