Problema geometria esame seconda superiore.

[Sgamber]

Mi hanno dato questo problema all'esame di riparazione del debito di stamattina solo che sono riuscita a risolverlo solo a metà e probabilmente me lo chiederanno domani all'orale. Potreste darmi una mano?

Dato un quadrilatero ABCD inscritto in una circonferenza di cui la diagonale AC è diametro della circonferenza, l'angolo DAC è di 45° e l'angolo CAB è di 30° trovare area e perimetro del quadrilatero.

Io con vari calcoli ho trovato che:

AD e DC misurano entrambi ''2 per r alla seconda'', il tutto sotto radice quadrata.
L'angolo ABC è di 90°, e quindi che l'angolo BCA è di 60°.
Il punto è E è il centro della circonferenza.

Grazie. (:

[romano90]

Ciao ^^

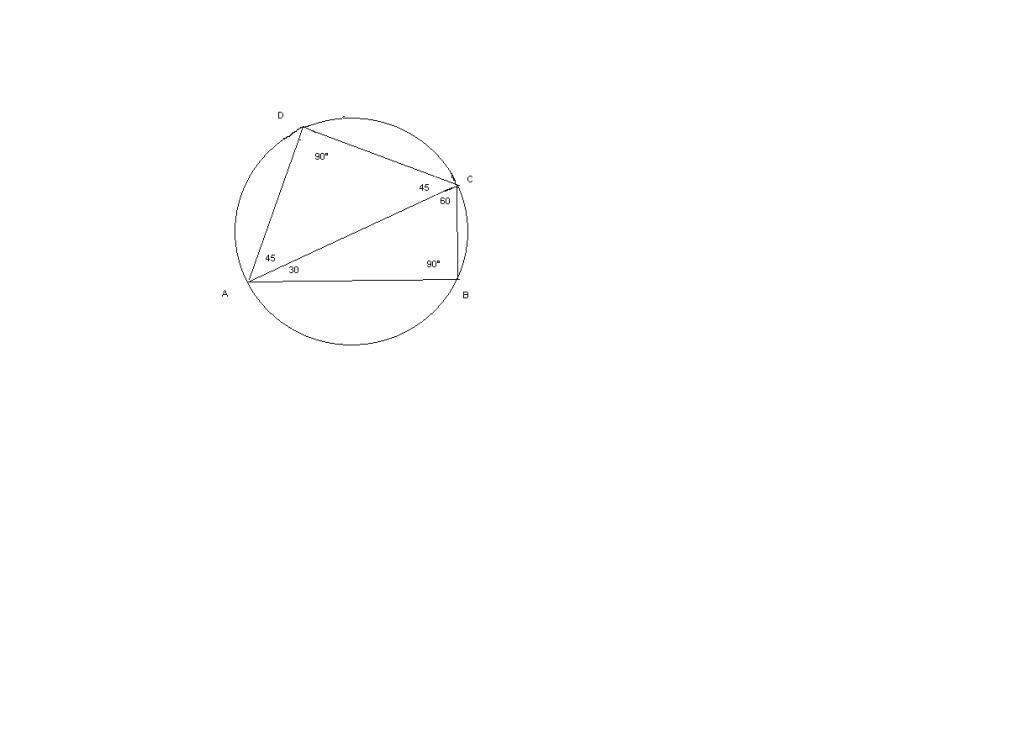
Li hai studiati seno e coseno giusto?

Dal testo del problema si capisce che il quadrilatero viene diviso dalla sua diagonale in 2 triangoli rettangoli (ogni triangolo inscritto in una semicirconferenza è rettangolo...)

Sapendo che:

[math] AC=2r[/math]

Ti puoi trovare tutti i lati del quadrilatero ( o dei 2 triangoli se ti è più semplice)

dal disegno che ho fatto ( non so se è giusto ma mi sembra di si...) gli angoli sono:
BCA=60° BAC=30° CBA=90° DCA=CAD=45° e CDA=90°


ti mancano DA, DC, CB e AB per il perimetro

AB=AC*sen60° =

[math]2r*\frac{\sqrt{3}}{2}= r\sqrt{3}[/math]

CB=AC*sen30° =

[math]2r*\frac{1}{2}= r[/math]

AD=AC*sen45° =

[math]2r*\frac{\sqrt{2}}{2}= r\sqrt{2}[/math]

CD=AC*sen45° =

[math]2r*\frac{\sqrt{2}}{2} =r\sqrt{2}[/math]

Cosi puoi calcolarti sia il perimetro (Sommi i 4 lati) e l'area ( calcolandoti le 2 aree dei triangoli (

[math]\frac{b*h}{2}[/math]

) e sommandole).

Ti ho messo il mio disegno...

[ciampax]

Romano, se fa il secondo superiore, dubito conosca la trigonometria! Per risolverlo basta applicare il Teorema di Pitagora: abbiamo

[math]AD=DC=\frac{AC}{\sqrt{2}}[/math]

ppoiché, essendo ADC triangolo rettangolo isoscele, risulta la metà di un quadrato. Analogamente

[math]BC=\frac{AC}{2},\qquad AB=\frac{\sqrt{3}}{2} AC[/math]

in quanto il triangolo ABC risulta la metà di un triangolo equilatero. Ne segue che

[math]AD=AC=r\sqrt{2},\quad BC=r,\quad AB=r\sqrt{3}[/math]

e quindi

[math]2p=2\cdot r\sqrt{2}+r+r\sqrt{3}=(2\sqrt{2}+\sqrt{3}+1)r[/math]

[math]S=\frac{1}{2}\cdot r\sqrt{2}\cdot r\sqrt{2}+\frac{1}{2}\cdot r\cdot r\sqrt{3}=
\frac{r^2}{2}(2+\sqrt{3})[/math]

Spero ti sia utile!

[romano90]

Ops, combino sempre macelli cercando di aiutare XDD

Scusa se ti ho confuso le idee Sgamber >.

[Sgamber]

Ma figurati!! Vi ringrazio tantissimo entrambi. (:

[mitraglietta]

bravo il nostro ciampolino. sempre pronto ad aiutare il prossimo, e bravo anche a romano che ha cercato di aiutare lo sventurato sgamber con questo problema, quindi proporrei di chiudere il thread che dite?

l'esercizio è stato egregiamente risolto.

[BIT5]

si, direi che si può chiudere