Problema di massimo e minimo

[gcappellotto]

Salve a tutti
ho delle difficoltà con il seguente problema:
Tra tutti i coni di dato volume $1/3 \pi a^3$ determinare quello di minima apotema.

Ho provato in questo modo:
Volume del cono: $V=(\pi r^2 h)/3$
altezza del cono: $h=\sqrt(a^2-r^2)$ quindi $V=\pi*r^2*\sqrt(a^2-r^2)/3=\pi a^3/3$
posso semplificare e ottengo:
$V=r^2*\sqrt(a^2-r^2)=a^3$
a questo punto si dovrebbe derivare però non credo sia corretto quanto ho svolto.
Ringrazio chi mi aiuterà.
Giovanni C.

[gcappellotto]

Quello che tu mi consigli non porta a un risultato corretto che dovrebbe essere altezza=$a/(2)^{1/3}$

[Gi81]

Credo che ci sia qualcosa che non va nell'esercizio.
Ti spiego: dall'ipotesi e dalla formula del volume di un cono si ha $pi/3 r^2 h = pi/3 a^3 => r^2 h= a^3$.
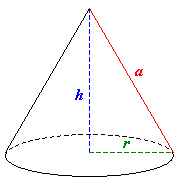
Ma $a^3> r^2*h$: infatti da $a^2=r^2+h^2$ si ha che $a> r$ e $a>h$ (puoi anche vedere dal disegno che l'apotema è certamente maggiore del raggio e anche dell'altezza), dunque $a^3=a*a*a> r*r*h=r^2 h$

Dunque non si può avere $r^2 h = a^3$, ovvero non si può avere $V= pi/3 a^3$.