Passaggio 2° prova, mat. trad., 2 problema
Sto guardando le soluzioni proposte da voi ma non riesco a capire come da quest'equazione: 
si ottenga:
Faccio tutti passaggi ma nn mi risulta..
Grazie a chiunque voglia darmi qualche chiarimento
:)

si ottenga:

Faccio tutti passaggi ma nn mi risulta..
Grazie a chiunque voglia darmi qualche chiarimento
:)
Risposte
Hai ragione, è un errore di trascrizione, ovviamente nella formula manca il seno (d'altronde, si chiama teorema dei seni apposta...). La formula corretta è
[math]\frac{r}{\sin \alpha} = \frac{l}{\sin\left(\pi- 2\alpha\right)} = \frac{l}{\sin 2\alpha}[/math]
Scusa Pillaus, non è che potresti farmi vedere qualche passaggio perchè non mi viene comunque.. Grazie e scusa il disturbo
Allora, scusa ma ho perso tempo a fare il disegno. Allora, il triangolo isoscele è ABC, e O è il centro della circonferenza. Considero BC la base del triangolo isoscele (quindi i lati obliqui AB e AC sono uguali). L'angolo in A lo chiamo
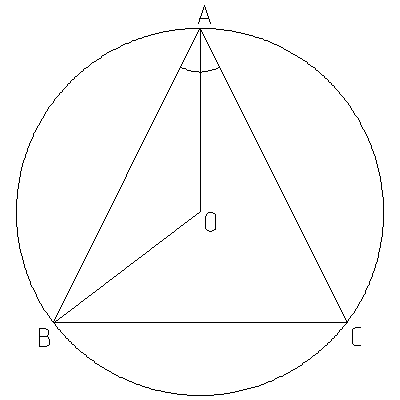
Ora, noi ci concentiamo sul triangolo AOB. Questo è isoscele, perché ha per lati uguali i due raggi AO e OB.
L'angolo BAO è per costruzione la metà dell'angolo BAC, quindi misura
Applichiamo il teorema dei seni al triangolo AOB. Questo dice che in un triangolo il rapporto tra la lunghezza di un lato e il seno dell'angolo opposto è costante per tutti e tre i lati. Lo applichiamo al lato AO e al lato AB.
Possiamo scrivere:
Ora:
- l'angolo AOB misura
-
- nel problema abbiamo chiamato AB = l e AO = OB = r
dunque:
da cui l'asserto
[math]2\alpha[/math]
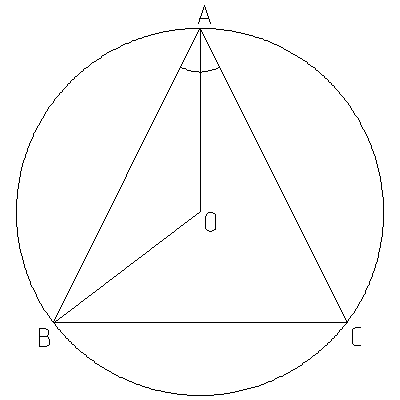
Ora, noi ci concentiamo sul triangolo AOB. Questo è isoscele, perché ha per lati uguali i due raggi AO e OB.
L'angolo BAO è per costruzione la metà dell'angolo BAC, quindi misura
[math]\alpha[/math]
Applichiamo il teorema dei seni al triangolo AOB. Questo dice che in un triangolo il rapporto tra la lunghezza di un lato e il seno dell'angolo opposto è costante per tutti e tre i lati. Lo applichiamo al lato AO e al lato AB.
Possiamo scrivere:
[math]\frac{AO}{\sin B \hat AO} = \frac{AB}{\sin A\hat OB}[/math]
Ora:
- l'angolo AOB misura
[math]\pi - B \hat AO - O \hat BA = \pi - 2B \hat AO = \pi - 2\alpha[/math]
(sfruttando che BAO=OBA, siccome il triangolo è isoscele);-
[math]\sin\left(\pi - x\right)=\sin x[/math]
- nel problema abbiamo chiamato AB = l e AO = OB = r
dunque:
[math]\frac{AO}{\sin B \hat AO} = \frac{AB}{\sin A\hat OB}\\
\frac{r}{\sin \alpha} = \frac{l}{\sin 2\alpha}[/math]
\frac{r}{\sin \alpha} = \frac{l}{\sin 2\alpha}[/math]
da cui l'asserto
Grazie Pillaus.. Sei stato molto chiaro ed esaustivo!
Io l'avevo anche detto a ciampax e sull'olimpo che era sbagliato, ma nessuno mi ha dato ascolto...:blush:cry
Vabbè dai chiudo questo thread!
Vabbè dai chiudo questo thread!
Questa discussione è stata chiusa


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo