Funzione crescente

[paperino001]

Salve, la funzione [tex]y= (\frac{1}{a^2+2})^x[/tex] al variare di [tex]a[/tex] se è crescente o descrescente dipende dalla x ?

[minomic]

Ciao, no questa funzione è sempre decrescente. Infatti si tratta di una esponenziale con la base che è sempre minore di $1$.
Questa cosa si capisce osservando il denominatore della base che è una somma tra $2$ e una quantità che non può valere meno di $0$, quindi la base sarà $1/2$ per $a=0$ o più piccola al crescere di $a$. In ogni caso la funzione è decrescente.
Ti torna?

[paperino001]

ma se la x è negativa la funzione non diventa crescente perchè l'uno va al denominatore ?

[minomic]

"paperino00":ma se la x è negativa la funzione non diventa crescente perchè l'uno va al denominatore ?

Capisco quello che vuoi dire, ma devi fare attenzione perchè dire "crescente" o "decrescente" presuppone comunque di muoversi verso destra, cioè nel verso positivo dell'asse $x$. Quindi per un valore negativo molto grande della $x$, ad esempio $x=-100$, il valore della funzione è enorme, poi quando la $x$ aumenta, il valore della funzione diminuisce sempre di più, fino ad arrivare a valori molto grandi della $x$, diciamo ad esempio $x=1000$, per i quali la funzione ha un valore che si avvicina allo zero. Per chiarezza posto il grafico della funzione $y=(1/3)^x$ che si ottiene dalla tua con il valore $a=1$.



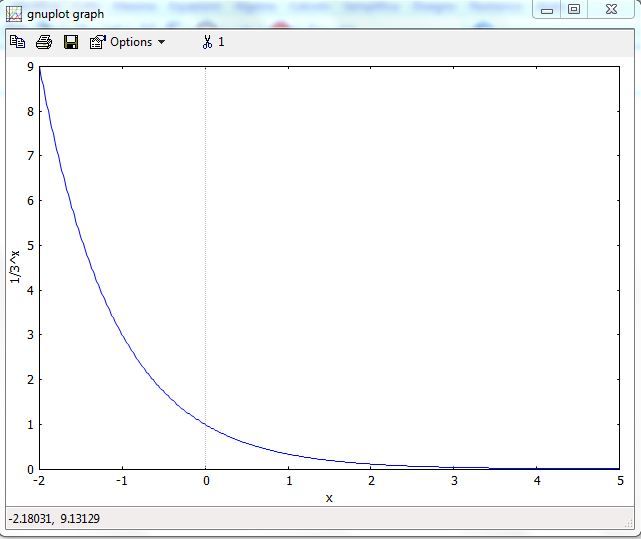
Fammi sapere se hai altri dubbi.