Dimostrazione di geometria (angoli e lati di un triangolo)

[iolanda.disimone]

Ciao a tutti, non riesco a risolvere questo esercizio, mi sono incartata non concludendo nulla.
Nella figura qui sotto, è noto per ipotesi che $\alpha < \beta$ e $\gamma < \delta$. Dimostra che $AD > CB$.


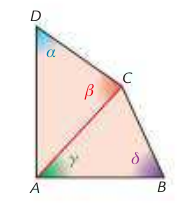
So che dovrei proporre un tentativo di risoluzione, ma la verità e che non so da dove iniziare. La teoria sulla disuguaglianza dei triangoli, che sono certa di dover utilizzare, non mi aiuta, nel senso che non so come applicarla. Penso dovrei dimostrare che $\beta$ è l'angolo maggiore e $\gamma$ il minore in modo da dimostrare che $AD$, in quanto opposto di $\beta$, è maggiore di $CB$, in quanto opposto di $\gamma$, ma non so come arrivarci
Potete aiutarmi?

[@melia]

Dal fatto che $ \gamma < \delta $ ricavi che $CB da $ \alpha < \beta $ ricavi $AC per la proprietà transitiva $CB

Cita

Segnala

[iolanda.disimone]

Non ci credo, così semplice? Io mi stavo incartando in chissà quali dimostrazioni!! Grazie mille, credo che potrò risolvere facilmente anche l'altro che ho postato seguendo le tue indicazioni, ora ci provo.