Curvatura media&minimi e massimi
ciao a tutti!!! è da un pò che non faccio un giro da queste parti...spero che l'anno sia iniziato bene per tutti!
lasciando da parte i convenevoli...ecco le domande che ho da porvi:
1- sapete dove posso trovare qualcosa che spieghi in maniera molto molto semplice i concetti di curvatura e curvatura media di una superficie??
2- devo trattare nella tesina il concetto dei minimi e dei massimi in una funzione...secondo voi da dove devo partire??mi suggerite di partire da che cos'è lo studio di una funzione e quindi studiare una funzione qualunque per arrivare a sviluppare il punto dei max e min in maniera esaustiva, o è meglio secondo voi spiegare subito i max e min, o altro ancora??
tenete presente che entrambe le domande mi servono per la tesina sulle BOLLE DI SAPONE devo perciò presentare gli argometni in maniera abbastanza semplice, abbastanza concisa e abbastanza coinvolgente visto che dovrò attirare l'attenzione anche di chi non ama la matematica!!
grazie!!!!!
margotz
lasciando da parte i convenevoli...ecco le domande che ho da porvi:
1- sapete dove posso trovare qualcosa che spieghi in maniera molto molto semplice i concetti di curvatura e curvatura media di una superficie??
2- devo trattare nella tesina il concetto dei minimi e dei massimi in una funzione...secondo voi da dove devo partire??mi suggerite di partire da che cos'è lo studio di una funzione e quindi studiare una funzione qualunque per arrivare a sviluppare il punto dei max e min in maniera esaustiva, o è meglio secondo voi spiegare subito i max e min, o altro ancora??
tenete presente che entrambe le domande mi servono per la tesina sulle BOLLE DI SAPONE devo perciò presentare gli argometni in maniera abbastanza semplice, abbastanza concisa e abbastanza coinvolgente visto che dovrò attirare l'attenzione anche di chi non ama la matematica!!
grazie!!!!!
margotz
Risposte
cara margotz
sono assai lieto di poterti aiutare nella tua tesi sulle bolle, che ha degli spunti veramente interessanti in moltissimi campi scientifici. Riguardo alla tua prima domanda ti consiglio vivamente di guardare in http://www.vialattea.net/curvatura/ … dove potrai trovare una fantastica trattazione della curvatura non solo delle curve [immerse in due dimensioni] o delle superfici [immerse in tre dimensioni] ma anche degli spazi [immersi in quattro dimensioni].
Volendo andare per gradi tuttavia ti consiglio di provare da prima ad affrontare il problema i due dimensioni. Prendendo pari pari dal sito che ti ho segnalato…

Se pensiamo ad una generica linea immersa in un piano, la curvatura è intuitivamente la misura di quanto essa devia rispetto alla tangente. Inoltre ci accorgiamo immediatamente che si tratta di una proprietà locale e non globale. In altre parole, ha senso definire la curvatura in un punto, ma non significa nulla parlare di ‘curvatura di una linea’.
La curvatura in un punto P si calcola come
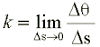 [1]
[1]
E’ facile verificare che la retta, in base a questa definizione, ha curvatura nulla. Pensiamo ora alla linea curva più semplice: la circonferenza. La sua curvatura è costante per tutti i punti e vale k=1/R. Come era logico aspettarsi, quanto maggiore è il raggio, tanto minore sarà la curvatura della circonferenza; inoltre se consideriamo la retta come una circonferenza di raggio infinito, ritroviamo consistentemente che la sua curvatura è zero.
Uno degli aspetti fondamentali delle bolle è il giustificare la loro forma, che, in assenza di particolari vincoli, risulta essere una sfera. Il motivo di ciò è che la sfera è la superficie che, a parità di volume, è minima o equivalentemente che a parità di area racchiude il volume massimo. Dal punto di vista della fisica la bolla obbedisce alla legge generale secondo la quale qualunque sistema isolato evolve verso la condizione di minima energia. Volendo per semplificare le cose affrontare il problema in due dimensioni è essenziale l’accenno al problema isoperimetrico .
Il problema isoperimetrico è di vecchia data [se lo pose per primo il filosofo-matematico greco Zenodoro]. Esso consiste nel trovare la curva piana che a parità di lunghezza racchiude l’area massima. Dal punto di vista rigorosamente matematico esso può essere impostato bel modo seguente…
Data una curva chiusa nel piano x,y essa può essere rappresentata con una coppia di equazioni parametriche…
x=x(t) , y=y(t) [2]
… in cui t è compreso nell’intervallo [t1,t2] ed è…
x(t1)= x(t2), y(t1)=y(t2) [3]
… il problema cosiste nel trovare x(t) ed y(t) in modo che, con il vincolo che la lunghezza della curva sia uguale ad l, vale a dire…
 [4]
[4]
… l’area A racchiusa dalla curva, data da…
 [5]
[5]
… sia massima. La soluzione, come si intuisce in base al buon senso, è un cerchio. Zenodoro a suo tempo dimostrò che l’area racchiusa in un cerchio è maggiore di quella di un qualsiasi poligono avente lo stesso perimetro. Il problema è stato risolto nel caso generale solo in tempi più recenti, allorché Steiner ha pubblicato nel 1841 la soluzione rigorosa del problema.
Credo così di averti dato un po’ di spunti iniziali sui quali potrai trovare ulteriori approfondimenti… in ogni caso se ti servirà aiuto io son sempre qui…
un cordiale saluto!…
lupo grigio

Modificato da - lupo grigio il 20/01/2004 09:53:39
sono assai lieto di poterti aiutare nella tua tesi sulle bolle, che ha degli spunti veramente interessanti in moltissimi campi scientifici. Riguardo alla tua prima domanda ti consiglio vivamente di guardare in http://www.vialattea.net/curvatura/ … dove potrai trovare una fantastica trattazione della curvatura non solo delle curve [immerse in due dimensioni] o delle superfici [immerse in tre dimensioni] ma anche degli spazi [immersi in quattro dimensioni].
Volendo andare per gradi tuttavia ti consiglio di provare da prima ad affrontare il problema i due dimensioni. Prendendo pari pari dal sito che ti ho segnalato…

Se pensiamo ad una generica linea immersa in un piano, la curvatura è intuitivamente la misura di quanto essa devia rispetto alla tangente. Inoltre ci accorgiamo immediatamente che si tratta di una proprietà locale e non globale. In altre parole, ha senso definire la curvatura in un punto, ma non significa nulla parlare di ‘curvatura di una linea’.
La curvatura in un punto P si calcola come
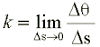 [1]
[1]E’ facile verificare che la retta, in base a questa definizione, ha curvatura nulla. Pensiamo ora alla linea curva più semplice: la circonferenza. La sua curvatura è costante per tutti i punti e vale k=1/R. Come era logico aspettarsi, quanto maggiore è il raggio, tanto minore sarà la curvatura della circonferenza; inoltre se consideriamo la retta come una circonferenza di raggio infinito, ritroviamo consistentemente che la sua curvatura è zero.
Uno degli aspetti fondamentali delle bolle è il giustificare la loro forma, che, in assenza di particolari vincoli, risulta essere una sfera. Il motivo di ciò è che la sfera è la superficie che, a parità di volume, è minima o equivalentemente che a parità di area racchiude il volume massimo. Dal punto di vista della fisica la bolla obbedisce alla legge generale secondo la quale qualunque sistema isolato evolve verso la condizione di minima energia. Volendo per semplificare le cose affrontare il problema in due dimensioni è essenziale l’accenno al problema isoperimetrico .
Il problema isoperimetrico è di vecchia data [se lo pose per primo il filosofo-matematico greco Zenodoro]. Esso consiste nel trovare la curva piana che a parità di lunghezza racchiude l’area massima. Dal punto di vista rigorosamente matematico esso può essere impostato bel modo seguente…
Data una curva chiusa nel piano x,y essa può essere rappresentata con una coppia di equazioni parametriche…
x=x(t) , y=y(t) [2]
… in cui t è compreso nell’intervallo [t1,t2] ed è…
x(t1)= x(t2), y(t1)=y(t2) [3]
… il problema cosiste nel trovare x(t) ed y(t) in modo che, con il vincolo che la lunghezza della curva sia uguale ad l, vale a dire…
 [4]
[4]… l’area A racchiusa dalla curva, data da…
 [5]
[5]… sia massima. La soluzione, come si intuisce in base al buon senso, è un cerchio. Zenodoro a suo tempo dimostrò che l’area racchiusa in un cerchio è maggiore di quella di un qualsiasi poligono avente lo stesso perimetro. Il problema è stato risolto nel caso generale solo in tempi più recenti, allorché Steiner ha pubblicato nel 1841 la soluzione rigorosa del problema.
Credo così di averti dato un po’ di spunti iniziali sui quali potrai trovare ulteriori approfondimenti… in ogni caso se ti servirà aiuto io son sempre qui…
un cordiale saluto!…
lupo grigio

Modificato da - lupo grigio il 20/01/2004 09:53:39
Per ora ti ringrazio moltissimo!
nel caso abbia bisogno di altri aiuti....ti farò sapere!
grazie ancora infinitamente!
margotz
nel caso abbia bisogno di altri aiuti....ti farò sapere!
grazie ancora infinitamente!
margotz


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo