Area triangolo

Quanto vale l'area del triangolo $ABC$?
Sinceramente mi ha spiazzato questo esercizio, perché se non facessi assunti sul tipo di triangolo non trovo un risultato corretto.
Prima di tutto traslo il triangolo sull'asse delle $x$, quindi A sarà centrato nell'origine per comodità.
Guardando la figura sembra che il triangolo sia rettangolo, quindi posso usare alcuni teoremi sugli angoli.
L'angolo in $A$ è rettangolo quindi $pi/2$, gli angoli esterni saranno di $pi/4$ ognuno.
Ora ho due triangoli rettangolo $AWC$ e $AVB$, con angolo in $A$ di $pi/4$.
$WA=2$
$CA=2/\cos(pi/4)=2\sqrt(2)$
$AV=5$
$AB=5/\cos(pi/4)=5\sqrt(2)$
Ora posso utilizzare la proprietà che l'altezza di un triangolo rettangolo può essere anche un cateto, quindi per calcolare l'area del triangolo $ABC$ ruoto il triangolo e metto in piano $AB$ utilizzando $AC$ come altezza.
AreaABC$ = (CA*AB)/2 = (2\sqrt(2)*5\sqrt(2))/2 = 10$
Il risultato però è sbagliato: è la risoluzione o proprio il metodo sbagliato?
Non avendo utilizzato tutti i dati presumo che ci sia una proprietà che non vedo e che si possa utilizzare, forse attraverso i trapezi oppure calcolando le rette passanti per punti? Mi dareste un spinta (non la soluzione)?
Grazie
Risposte
A mio avviso l'area è facilissima da calcolare, proprio con il metodo proposto da TeM. Non mi trovo con il risultato, perché dividendo il triangolo in due parti, l'una con base 3 lungo l'asse delle ordinate e altezza 5 misurata in ascissa, l'altra con la stessa base e altezza $|-2|=2$, ottengo
$(3*5)/2 + (3*2)/2=7,5+3=10,5$
PS: mi correggo, avevo letto male il valore dell'area, che pure mi risulta uguale a quella di TeM. Intervento ridondante quindi, direi una tautologia, ma dopo averlo scritto con interesse e passione, lo posto ugualmente.

Ciao a tutti.
Marco
$(3*5)/2 + (3*2)/2=7,5+3=10,5$
PS: mi correggo, avevo letto male il valore dell'area, che pure mi risulta uguale a quella di TeM. Intervento ridondante quindi, direi una tautologia, ma dopo averlo scritto con interesse e passione, lo posto ugualmente.

Ciao a tutti.
Marco
grazie ad entrambi!
ma dai, vedo ora...
Alcune curiosità:
- te proponi la somma, però calcolando direttamente $WV*(OD-1)/2 = (7*3)/2$ ritorna il risultato; perché?
- la formula dell'area sui triangoli generici è applicabile solo se la base è in piano e l'altezza (perpendicolare) è, indifferentemente, interna od esterna cioè solo se:
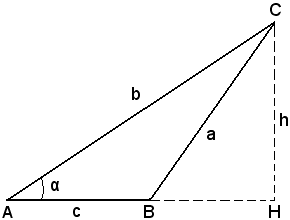
Domando: se ruotassi la figura sopra di 90 gradi in senso orario, ed avessi ora $AB$ come altezza e $CH$ come base, potrei fare le stesse considerazioni geometriche, cioè la formula rimarrebbe corretta?
Considerando la commutatività della moltiplicazione direi di sì, ma forse geometricamente la formula è sbagliata...
su $A$ che sia o meno retto non dubito, invece l'angolo in WAC e VAB sì che ero sicuro...mannaggia agli errori.
"TeM":
In particolare, nel caso proposto, detto D il punto di coordinate (0; 4), l'area del generico triangolo ABC la si può calcolare sommando l'area del generico triangolo ABD e l'area del generico triangolo ACD, utilizzando in entrambi casi la nota formula "base per altezza diviso due", ottenendo 10,5.
ma dai, vedo ora...
Alcune curiosità:
- te proponi la somma, però calcolando direttamente $WV*(OD-1)/2 = (7*3)/2$ ritorna il risultato; perché?
- la formula dell'area sui triangoli generici è applicabile solo se la base è in piano e l'altezza (perpendicolare) è, indifferentemente, interna od esterna cioè solo se:

Domando: se ruotassi la figura sopra di 90 gradi in senso orario, ed avessi ora $AB$ come altezza e $CH$ come base, potrei fare le stesse considerazioni geometriche, cioè la formula rimarrebbe corretta?
Considerando la commutatività della moltiplicazione direi di sì, ma forse geometricamente la formula è sbagliata...
"TeM":
Che poi ABC sia rettangolo in A è tutto da dimostrare, non lo
si può dedurre ad occhio, dato che se un disegno non è scalato opportunamente è molto difficile capirlo, ma comunque
ai fini dell'esercizio non interessa. Ultima cosa, e concludo, traslando A in O e assumendo che l'angolo CAB sia retto, non
è detto che gli angoli WAC e VAB siano entrambi la metà, è certo solamente che la loro somma sia pari ad un angolo retto.
Spero sia sufficientemente chiaro.
su $A$ che sia o meno retto non dubito, invece l'angolo in WAC e VAB sì che ero sicuro...mannaggia agli errori.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo