Area rettangolo da massimizzare

[vanpic]

Buongiorno
nel triangolo qualsiasi ABC manda la parallela al lato AB che interseca i lati AC e BC rispettivamente nei punti G e F. Indicate con D ed E le proiezioni ortogonali di G ed F sulla retta del lato AB, determina il rettangolo DEFG di area massima.

non riesco ha trovare una relazione, in una variabile, che lega i lati del rettangolo la cui area è da massimizzare.
Potreste darmi un suggerimento?
Grazie.

[Quinzio]

Tante vole nella matematica, come per altro nella vita in generale, bisogna cercare un po' di "farsi furbi".
Per cui, siccome ci hanno detto che il triangolo ABC e' un triangolo qualsiasi, e allora il disegno e' solo un esempio, ma perche' non scegliere un triangolo "facile" come ad esempio un triangolo rettangolo con l'angolo retto in A, e, finche' ci siamo, con i cateti AC e AB uguali ?
E perche' no, mettiamo AB e AC di lunghezza 1.
Poi, potremmo disegnare il triangolo su un piano cartesiano, con i cateti sugli assi xy.
A questo punto, se la distanza DE diventa $k$, DG diventa $1-k$, l'area del rettangolo e' $k(1-k)$, e poi....

[gugo82]

Già... Però poi devi affrontare il caso generale comunque.

Se fosse lecito usare le affinità, la faccenda sarebbe semplice: basterebbe usare un determinante.

[utente__medio11]

Premetto che sono molto arrugginito su queste cose, ma con questa impostazione mi sembra che il problema diventi abbastanza agevole:



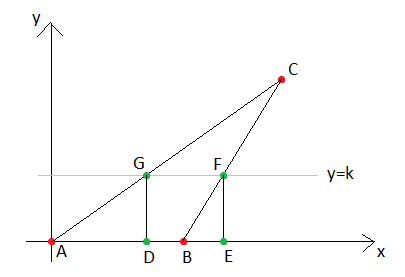
Una volta scritta l'equazione della retta passante per $A$ e $C$, e della retta passante per $B$ e $C$, le mettiamo a sistema con la retta orizzontale $y=k$ (con $0 A questo punto l'area del rettangolo, pari a $k(x_F-x_G)$, sarà una funzione di secondo grado nella variabile $k$, e dall'annullamento della sua derivata prima si ottiene il valore di $k$, e quindi il rettangolo, ricercato.

Provando a fare velocemente i conti mi viene $k=y_C/2$, fammi sapere se ti torna.

[@melia]

Non ho fatto i conti, ma se si ottiene una funzione di secondo grado in $k$, non servono le derivate, basta trovare il vertice della parabola.

[giammaria2]

A me sembra che usare l'analitica per questo problema sia come usare un cannone per ammazzare un moscerino: bastano armi molto meno potenti ed uso la similitudine.
Mi piacw vedere AB iin orizzontale, quindi mi riferisco alla figura di utente_medio,alla quale aggiungo l'altezza CH relativa ad AB; chiamo K l'interwzione delle rette CH, GF e pongo $AB=a;CH=h;CK=x$,
Dalla similitudine di FKC, BHC ho $CK: CH=CF:CB$
Dalla similitudine di GFC, ABC ho $GF=AB=CF:CB$
I due secondi membri sono uguali, quindi devono esserlo anche i primi; ottengo
$CK:CH=GF:AB->x:h=GF:a->GF=(ax)/h$
L'area da massimizzare è quindi
$S=GF*GD=GF*(CH-CK)= a/h x(h-x)$
e si conclude facilmente anche con metodi elementari, fra cui quello indicato da @meluia.