Area Fiocco di neve di Koch

[magikarpown]

Ciao a tutti! Ieri nell' ora di matematica mi ero rotto di fare quegli stupidi problemi, allora visto che ho appena letto un libro che parla dei frattali, mi sono messo a calcolare l' area del Fiocco di neve di Koch.

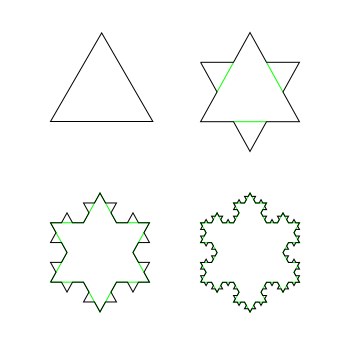
Sono partito dall' area del triangolo (equilatero) iniziale:

$Area=(B^2 sqrt3):2$

dove B è la base del triangolo iniziale.

Poi ho scoperto che a ogni aggiunta, la figura si ingrandisce di un terzo.

Quindi:

$Area F=(B^2 sqrt3):2+1/3 (B^2 sqrt3):2+1/9 (B^2 sqrt3):2...$

Dove Area F è l' area frattale che uscirà alla fine.
1+1/3+1/9+1/27+1/81 (fino a infinito) fa: 1+1/2=3/2

Da questo si ottiene:

$Area F=3/2 (B^2 sqrt3):2$

$Area F=3/4 (B^2 sqrt3)$

$Area F=(3 sqrt3 B^2)/4$

Potrebbe essere coerente?
(non uccidetemi se ho sbagliato )

[giannirecanati]

Riporto quello che wiki dice. http://it.wikipedia.org/wiki/Curva_di_Koch.

[magikarpown]

Mi puoi riassumere in termini un po' piu comprensibili? Purtroppo non so fare i limiti (vado alle medie).

[scrittore1]

E' corretto che l'area cresce di 1/3 ad ogni evoluzione della figura.

Avevo considerato che si partiva dal triangolo di area = 1
Avevo trovato (spero sia giusto) che l'area allo stadio N (se N=0 è il triangolo) è data da:

$A(n)=1+3/5[1-(4/9)^n]$ per ogni $n>=1$

Ponendo il limite $n->infty$ si ottiene $A(n)=1+3/5=1.6$
E di questo sono certo. Ossia, sono certo che l'area del fiocco di Koch è 1.6 volte l'area del triangolo originario.

[magikarpown]

Ah Ok ma perchè $1-(4/9)^n$? (Scusa l' ignoranza)

[scrittore1]

@magikarpown , quello che tu mi chiedi è il frutto di lunghi calcoli che sinceramente non ho voglia di stare a scrivere. Può darsi che giannirecanati abbia utilizzato un metodo più breve arrivando allo stesso risultato, ma per me il giro è stato tortuoso.

[magikarpown]

Ah ok fa lo stesso, grazie