Arco di una circonferenza
Problema stupido come si calcola la lunghezza di un arco di una circonferenza e la sua area
si risolve con una semplice proporzione lo so
360 : angolo della corda = 2 pigraca r : lunghezza corda
oppure e questo nn so
2 pigreca : angolo della corda in radianti = 2 pigreca r : lunghezza corda
Lo stesso vale per l`area ma quele proporzione e` corretta e` perche
la stessa domanda vale per la proporzione che mi consente di calcolare l`area
si risolve con una semplice proporzione lo so
360 : angolo della corda = 2 pigraca r : lunghezza corda
oppure e questo nn so
2 pigreca : angolo della corda in radianti = 2 pigreca r : lunghezza corda
Lo stesso vale per l`area ma quele proporzione e` corretta e` perche
la stessa domanda vale per la proporzione che mi consente di calcolare l`area
Risposte
Scusami, ma non ho capito.
Interpreto:
Problema stupido come si calcola la lunghezza di un arco di una circonferenza e la sua area
si risolve con una semplice proporzione lo so
360 : angolo della corda = 2 pigraca r : lunghezza corda
oppure e questo nn so
2 pigreca : angolo della corda in radianti = 2 pigreca r : lunghezza corda
Lo stesso vale per l'area ma quale proporzione è corretta e perché?
la stessa domanda vale per la proporzione che mi consente di calcolare l'area
Problema stupido come si calcola la lunghezza di un arco di una circonferenza e la sua area
si risolve con una semplice proporzione lo so
360 : angolo della corda = 2 pigraca r : lunghezza corda
oppure e questo nn so
2 pigreca : angolo della corda in radianti = 2 pigreca r : lunghezza corda
Lo stesso vale per l'area ma quale proporzione è corretta e perché?
la stessa domanda vale per la proporzione che mi consente di calcolare l'area
"raff5184":
Interpreto:
Problema stupido come si calcola la lunghezza di un arco di una circonferenza e la sua area
si risolve con una semplice proporzione lo so
360 : angolo della corda = 2 pigraca r : lunghezza corda
oppure e questo nn so
2 pigreca : angolo della corda in radianti = 2 pigreca r : lunghezza corda
Lo stesso vale per l'area ma quale proporzione è corretta e perché?
la stessa domanda vale per la proporzione che mi consente di calcolare l'area
Ti sei dato alle traduzioni, raff?


Comunque continua a non essermi chiara la domanda; sarò scemo io, non so (probabile, eh, mi conosco
scusate lo rispiego
allora semplicemente
Come si calcola la Lunghezza dell'arco
Come si calcola la Area del settore circolare
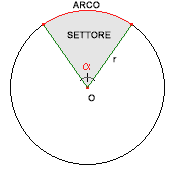
E poi come si ricavano le due formule?
allora semplicemente
Come si calcola la Lunghezza dell'arco
Come si calcola la Area del settore circolare

E poi come si ricavano le due formule?
Due proporzioni.
Chiamiamo $x$ la lunghezza dell'arco, e $alpha$ l'angolo al centro.
Ovviamente la circonferenza $2pir$ ha come angolo al centro un angolo giro $2pi$, quindi diciamo
$frac{2pir}{2pi}=frac{x}{alpha}$ da cui ottieni la formula, facile da ricordare,
$x=r*alpha$
Per l'area del settore è lo stesso.
Chiamiamo $S$ quest'area, e abbiamo
$frac{pir^2}{2pi}=frac{S}{alpha}$ da cui, facilmente,
$S=frac{alpha*r^2}{2}$
E' tutto chiaro?
Ciao.
Chiamiamo $x$ la lunghezza dell'arco, e $alpha$ l'angolo al centro.
Ovviamente la circonferenza $2pir$ ha come angolo al centro un angolo giro $2pi$, quindi diciamo
$frac{2pir}{2pi}=frac{x}{alpha}$ da cui ottieni la formula, facile da ricordare,
$x=r*alpha$
Per l'area del settore è lo stesso.
Chiamiamo $S$ quest'area, e abbiamo
$frac{pir^2}{2pi}=frac{S}{alpha}$ da cui, facilmente,
$S=frac{alpha*r^2}{2}$
E' tutto chiaro?
Ciao.
"antonio0290":
scusate lo rispiego
allora semplicemente
Come si calcola la Lunghezza dell'arco
Come si calcola la Area del settore circolare
E poi come si ricavano le due formule?
Ti ringrazio molto, ora comincio a capire. Vediamo un po':
I. Calcolo lunghezza arco.
Io imposterei la proporzione $2\pi:2\pir=\alpha:\mbox{arco}$ cioè $mbox{arco}=\frac{alpha*2\pir}{2\pi}=\alphar$. Occhio, devi mantenere coerenza con le unità di misura (angoli o tutti in gradi o tutti in radianti).
II. Calcolo area.
Stessa solfa anche qui: $2pi:alpha=pir^2:\mbox{area settore circolare}$ da cui...
Non so se è corretto. Prova, poi, se hai ancora bisogno, siamo qua.
No, no, no... bruciato per due minuti dal moderatore! 
P.S. @ il mitico Steven.. Come va, maturando?

P.S. @ il mitico Steven.. Come va, maturando?
In una qualsivoglia circonferenza $\Gamma$, preso un punto $C$ e un arco che lo contiene (diremo $ACB$ tale arco), risultano determinati senza ambiguità l'angolo al centro $AOB$ che insiste sull'arco, la corda $AB$ che lo sottende e il segmento circolare di base $AB$ che contiene $C$: per questo si dice che questi "pezzi" di circonferenza sono in corrispondenza.
Questi enti prendono il nome di elementi della circonferenza, e ciascuno di essi costituisce una classe di grandezze.
Si prova poi che, se sussiste una relazione di congruenza (denoteremo con $~=$ tale relazione) tra due grandezze della stessa classe, allora la medesima relazione sussiste tra gli altri elementi della circonferenza (la dimostrazione si basa sui movimenti rigidi: spostamenti nel piano di figure geometriche tali da mantenerne inalterate tutte le poprietà (su questi movimenti si può anche impostare la dimostrazione del primo principio di congruenza tra triangoli.
Il precedente fatto si usa per provare che le classi di grandezza di cui fin quì si è parlato sono classi di grandezze direttamente proporzionali.
La proporzione tra grandezze transita sulle misure (fissate in modo opportuno le unità di misura), da cui le formule date dagli amici Steven e Paolo90.
Questi enti prendono il nome di elementi della circonferenza, e ciascuno di essi costituisce una classe di grandezze.
Si prova poi che, se sussiste una relazione di congruenza (denoteremo con $~=$ tale relazione) tra due grandezze della stessa classe, allora la medesima relazione sussiste tra gli altri elementi della circonferenza (la dimostrazione si basa sui movimenti rigidi: spostamenti nel piano di figure geometriche tali da mantenerne inalterate tutte le poprietà (su questi movimenti si può anche impostare la dimostrazione del primo principio di congruenza tra triangoli.
Il precedente fatto si usa per provare che le classi di grandezza di cui fin quì si è parlato sono classi di grandezze direttamente proporzionali.
La proporzione tra grandezze transita sulle misure (fissate in modo opportuno le unità di misura), da cui le formule date dagli amici Steven e Paolo90.
x=r⋅α
S=(S=α⋅r)/2
Si ci ero arrivato anche io ma, allora scusate perche nel formulario li mette in maniera diversa?
https://www.matematicamente.it/formulari ... 812012329/
dove sta settore circolare mica le mette cosi e nn semplifica perche????
cmq grazie molte per laiuto
S=(S=α⋅r)/2
Si ci ero arrivato anche io ma, allora scusate perche nel formulario li mette in maniera diversa?
https://www.matematicamente.it/formulari ... 812012329/
dove sta settore circolare mica le mette cosi e nn semplifica perche????
cmq grazie molte per laiuto
Perché Steven e Paolo90 te le hanno fornite in radianti, mentre il nostro sito le mette in gradi sessagesimali.
Se le fai in gradi sessagesimali ottieni le proporzioni
(1) $2pi r : 360° = l : alpha => l=(2pi r alpha)/(360°)=(2 pi r alpha)/(2*180°)=(pi r alpha)/(180°)$
(2) $pi r^2 : 360° = A : alpha => A=(pi r^2 alpha)/(360°)$.
Se le fai in gradi sessagesimali ottieni le proporzioni
(1) $2pi r : 360° = l : alpha => l=(2pi r alpha)/(360°)=(2 pi r alpha)/(2*180°)=(pi r alpha)/(180°)$
(2) $pi r^2 : 360° = A : alpha => A=(pi r^2 alpha)/(360°)$.
"antonio0290":
scusate lo rispiego
allora semplicemente
Come si calcola la Lunghezza dell'arco
Come si calcola la Area del settore circolare
E poi come si ricavano le due formule?
Come hai fatto ad inserire la figura?
@franced
Copia il link alla figura (magari dopo averla caricata su imageshack - in questo caso copia il link che compare alla voce Direct link to image) e incollalo nel tuo messaggio tra [img]e[/img] senza lasciare spazi tra lìinizio del link e [img],%20né%20tra%20la%20fine%20del%20link%20e[/img].
Copia il link alla figura (magari dopo averla caricata su imageshack - in questo caso copia il link che compare alla voce Direct link to image) e incollalo nel tuo messaggio tra [img]e[/img] senza lasciare spazi tra lìinizio del link e [img],%20né%20tra%20la%20fine%20del%20link%20e[/img].
La cosa si spiega considerando che l'angolo giro si può esprimere sia in gradi che in radianti:
$360° = 2pi$
Se il tuo angolo $alpha$ lo esprimi in gradi allora nella formule ti apparanno termini come $360$ e $180$ da mettere in proporzione con la formule di area e circonferenza del cerchio.
Se invece il tuo angolo $alpha$ lo esprimi in radianti... allora nelle formule compaiono termini relativi a $2pi$ e $pi$ e dove il termine $pi$ viene eliminato fra numeratore e denonimatore.
Ecco il perché l'espressione varia a seconda se si considerano gradi e radianti. In semplicità:
$A_settore = A_cerchio * (gradi_settore / 360) = A_cerchio * (radianti_settore / 2pi)$
$L_arco = L_cerchio * (gradi_arco / 360) = L_cerchio * (radianti_arco / 2pi)$
P.S.: questo thread è una gara sul tempo...
$360° = 2pi$
Se il tuo angolo $alpha$ lo esprimi in gradi allora nella formule ti apparanno termini come $360$ e $180$ da mettere in proporzione con la formule di area e circonferenza del cerchio.
Se invece il tuo angolo $alpha$ lo esprimi in radianti... allora nelle formule compaiono termini relativi a $2pi$ e $pi$ e dove il termine $pi$ viene eliminato fra numeratore e denonimatore.
Ecco il perché l'espressione varia a seconda se si considerano gradi e radianti. In semplicità:
$A_settore = A_cerchio * (gradi_settore / 360) = A_cerchio * (radianti_settore / 2pi)$
$L_arco = L_cerchio * (gradi_arco / 360) = L_cerchio * (radianti_arco / 2pi)$
P.S.: questo thread è una gara sul tempo...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo