2 Esercizi da risolvere
Salve, ho dei problemi nel risolvere questi due esercizi; vi pregherei di elencarmi i passaggi in modo tale che possa capirli e ultimare in futuro consegne di questo genere.
Aggiunto 4 ore più tardi:
Salve, la ringrazio per la risposta a me data; vi è un inconveniente, però: il primo esercizio non chiede di essere risolto graficamente, bensì il secondo. Difatti, il primo chiede solo quando il trinomio è maggiore/uguale a zero (da risolvere con il tradizionale metodo) , mentre il secondo è un trinomio cui si chiede che valori avesse qualora fosse =, >, < di zero (da risolvere con il metodo grafico analitico). Spero di non crearle disturbo.
Aggiunto 4 ore più tardi:
Salve, la ringrazio per la risposta a me data; vi è un inconveniente, però: il primo esercizio non chiede di essere risolto graficamente, bensì il secondo. Difatti, il primo chiede solo quando il trinomio è maggiore/uguale a zero (da risolvere con il tradizionale metodo) , mentre il secondo è un trinomio cui si chiede che valori avesse qualora fosse =, >, < di zero (da risolvere con il metodo grafico analitico). Spero di non crearle disturbo.
Risposte
Vediamo il primo insieme, poi provi a fare il secondo:
Allora, devi vedere quando quel trinomio è maggiore o uguale a 0.
Per prima cosa, dobbiamo trovare le radici dell'equazione associata:
Questi sono i punti in cui la nostra parabola incontra l'asse delle x.
Ora sappiamo che la concavità della parabola dipende dal coeffciente del termine di secondo grado:
Se a > 0 , concavità verso l'alto (parabola che "sorride"...)
Se a < 0, concavità verso il basso (parabola "triste")
Noi dobbiamo vedere quando la parabola è sopra l'asse x (la disequazione chiedeva maggiore o uguale a 0).
La nostra parabola ha concavità verso il basso, quindi:
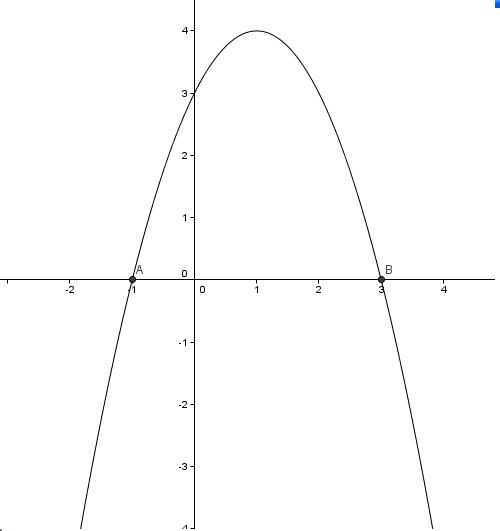
Come vedi, la parabola sta sopra l'asse x per valori compresi tra le radici:
quindi:
Se avessimo avuto la parabola con a > 0, i valori sarebbero stati esterni, in quanto tutta la parabola sarebbe capovolta.
Ora prova con il secondo...
Aggiunto 4 ore 20 minuti più tardi:
Non darmi del lei, mi fai sentire vecchio e ho solo qualche anno in più di te... siamo (quasi :asd) tutti ragazzi qui :)
Sinceramente, metodo grafico o no, io ho sempre risolto le disequazioni in questa maniera.
Ti ho postato l'immagine della parabola per farti avere chiaro il concetto di soluzioni esterne o soluzioni interne.
Se poi lo sai fare a mente, meglio per te :)
Comunque se era il secondo a dover essere risolto nel modo in cui ho risolto il primo, provaci e se non riesci posta il tuo dubbio. Se posso cercherò di chiartirtelo. :)
[math]-x^2+2x+3 \ge 0[/math]
Allora, devi vedere quando quel trinomio è maggiore o uguale a 0.
Per prima cosa, dobbiamo trovare le radici dell'equazione associata:
[math]-x^2+2x+3 = 0 \\ x_{1,2} = \frac{-2 \pm \sqrt{4+12}}{-2} \\ x_1= -1 \; x_2=3[/math]
Questi sono i punti in cui la nostra parabola incontra l'asse delle x.
Ora sappiamo che la concavità della parabola dipende dal coeffciente del termine di secondo grado:
Se a > 0 , concavità verso l'alto (parabola che "sorride"...)
Se a < 0, concavità verso il basso (parabola "triste")
Noi dobbiamo vedere quando la parabola è sopra l'asse x (la disequazione chiedeva maggiore o uguale a 0).
La nostra parabola ha concavità verso il basso, quindi:

Come vedi, la parabola sta sopra l'asse x per valori compresi tra le radici:
quindi:
[math]-1 \le x \le 3[/math]
Se avessimo avuto la parabola con a > 0, i valori sarebbero stati esterni, in quanto tutta la parabola sarebbe capovolta.
Ora prova con il secondo...
Aggiunto 4 ore 20 minuti più tardi:
Non darmi del lei, mi fai sentire vecchio e ho solo qualche anno in più di te... siamo (quasi :asd) tutti ragazzi qui :)
Sinceramente, metodo grafico o no, io ho sempre risolto le disequazioni in questa maniera.
Ti ho postato l'immagine della parabola per farti avere chiaro il concetto di soluzioni esterne o soluzioni interne.
Se poi lo sai fare a mente, meglio per te :)
Comunque se era il secondo a dover essere risolto nel modo in cui ho risolto il primo, provaci e se non riesci posta il tuo dubbio. Se posso cercherò di chiartirtelo. :)
ok..furor si riferisce ad un metodo di risoluzione più meccanico lontano da qualsiasi intuizione geometrica (che comunque a mio avviso è particolarmente importante). Detto questo puoi procedere nel modo che ho già spiegato in questo topic:
https://forum.skuola.net/matematica/math-superiori/disequazioni-di-secondo-grado-aiuto-46197.html#bottom
https://forum.skuola.net/matematica/math-superiori/disequazioni-di-secondo-grado-aiuto-46197.html#bottom


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo