Geometria (277938)

[mimsve.pix]

Calcola la misura di ciascun lato obliquo di un trapezio isoscele che ha l'area di 297 cmq, l'altezza di 9 cm e la base minore di 21 cm.
Grazie mille

[tiscali]

Anzitutto carico un'immagine così che tu possa meglio orientarti.





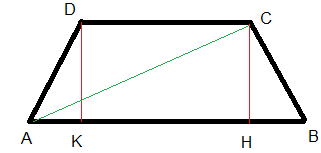
Siamo a conoscenza di determinate misure relative al trapezio:

[math]A = 297 cm^2[/math]

[math]DC = 21 cm[/math]

[math]DK = 9 cm[/math]

Il testo richiede il calcolo dei lati obliqui (in realtà è sufficiente calcolare la misura di uno solo dei due, poiché aventi la stessa misura. Prima di tutto occorre calcolare la misura della base maggiore AB. Per far ciò utilizziamo la formula inversa dell'area del trapezio:

[math]AB = \frac{A \cdot 2}{DK} - DC[/math]

sostituiamo i valori:

[math]AB = \frac{297 \cdot 2}{9} - 21 \to \frac{594}{9} - 21 \to 66 - 21 = 45 cm[/math]

Per calcolare il lato obliquo CA (o CB) possiamo applicare il teorema di Pitagora. Osserviamo che il triangolo DAK è rettangolo, per cui al fine di calcolare CA (ipotenusa di DAK) ci occorre la misura del segmento AK. Per misurarlo, sottraiamo dalla base maggiore AB la base minore DC, dopodiché dividiamo per due:

[math]AK = \frac{AB - DC}{2} = \frac{45 - 21}{2} = 12 cm[/math]

Adesso possiamo applicare il teorema di Pitagora per calcolare il lato obliquo DA:

[math]DA = \sqrt{AK^2 + DK^2} = \sqrt{12^2 + 9^2} = \sqrt{144 + 81} \to \sqrt{225} = 15 cm[/math]

Tutto chiaro?