Cilindro e cono

[fausto1947]

Buona sera,
non riesco a trovare la dimostrazione relativa al rapporto di volume di 1/3 esistente tra cono e cilindro.
Fausto

[moccidentale]

.

[fausto1947]

Grazie per la pronta risposta che già conoscevo.
Pensavo che esistesse una dimostrazione che non utilizzasse sommatorie o integrali e quindi più consona a dei ragazzi delle scuole medie.
Chiedo scusa del disturbo
Fausto

[lucastamba]

Ciao! Si potrebbe vedere anche in questo modo:
1) si può dividere un cubo in tre piramidi a base quadrata di volume equivalente, quindi il volume di ciascuna piramide è 1/3 di quello del cubo

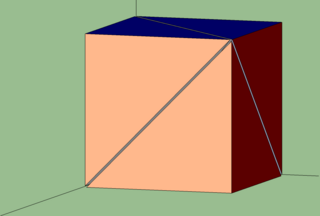
2) si può allungare il cubo lungo la sua altezza ottenendo un parallelepipedo a base quadrata. Le tre piramidi del punto precedente risulteranno anch'esse deformate ma il rapporto tra volumi rimane invariato, cioè sempre pari a 1/3 del volume del parallelepipedo
3) si può ottenere un cono con lo stesso volume di una piramide a base quadrata se si prende la stessa altezza e la stessa area di base (principio di Cavalieri)
4) si può ottenere un cilindro con lo stesso volume di un parallelepipedo a base quadrata se si prende la stessa altezza e la stessa area di base
5) si conclude che il cono ha volume pari a 1/3 del volume del cilindro con stessa area di base e stessa altezza :)

[fausto1947]

Grazie.
Si, sono soluzioni già più facilmente spiegabili ad uno studente delle medie.
Fausto

[axpgn]

Sinceramente tra il principio di Cavalieri e gli integrali come somma di infiniti pezzi non è che ci veda chissà quale differenza
Quello che ti ha spaventato è la certosina formalizzazione di sellacollesella

[moccidentale]

.

[@melia]

Ho un vago ricordo di un cono e un cilindro cavi, con ugual base e altezza, si riempiva d’acqua il cilindro e poi si verificava che con quell’acqua si poteva riempire 3 volte il cono.