Blocchi su piano inclinato

[75america]

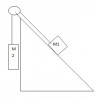
Due blocchi di massa m1=50kg e m2=100kg sono collegati come in figura.
La carrucola è di massa trascurabile e priva di attrito, il piano è inclinato di un angolo pigreco/6 rispetto all'orizzontale,
il coefficiente di attrito dinamico tra corpo1 e piano è uk=0.250. Determinare la variazione di enegia cinetica del corpo1 se sale di 20m. Determinare il tempo necessario se parte da fermo.

Ho provato a risolverlo così:
Diagramma delle forze:

${\(T-m_1gsentheta-u_dm_1gcostheta=m_1a),(m_2g-T=m_2a):}$
$-m_1gsentheta-udm_1gcostheta+m_2g=(m_1+m_2)a$

$(-245-106.6+980)/150=a$
$a=628.4/150=4.18m/s^2$

Conoscendo spazio percorso 20m e considerando velocità $v_0$ nulla applico la legge oraria del moto rett. unif. accelerato:
$x(t)=x_0+v_0t+1/2at^2$
$20=4.18/2 t^2$
$t=3.09s$

Calcolo velocità al momento del raggiungimento dei 20m:
$v=v_0+at$
$v=4.18*3.09=13m/s$
Variazione Energia Cinetica:
$1/2 m_1v^2=25*169=4425J$

Ci ho provato, ma credo di aver sbagliato...,spero nel vostro aiuto

[ciampax]

Dunque: sul corpo che scivola sul piano, lungo il piano stesso, agiscono tre forze: la componente della forza peso tangente al piano, la forza di attrito e la tensione della corda. Per cui possiamo scrivere

[math]T-m_1 g\sin\theta-\mu_d m_1 g\cos\theta=m_1 a_1[/math]

Per quanto riguarda il corpo sospeso, invece, direi che abbiamo la situazione seguente

[math]T-m_2 g=m_2 a_2[/math]

Ovviamente, se la fune è inestensibile, le due accelerazioni coincidono, pertanto possiamo scrivere

[math]T=m_2(a+g)[/math]

da cui

[math]m_2(a+g)-m_1 g\sin\theta-\mu_d m_1 g\cos\theta=m_1 a[/math]

e quindi

[math]a=\frac{m_1 g(\sin\theta+\mu_d\cos\theta)-m_2 g}{m_1+m_2}[/math]

Il resto mi sembra corretto, controlla solo che sia quello che ho scritto io il valore dell'accelerazione che hai trovato, perché non riesco a leggere bene.