FUNZIONE ERF(x)
Heila!!!!
volevo raccogliere tutte le informazioni possibili
sulla funzione ERF(x)! soprattutto su una sua possibile
approssimazione su tutto R (mi spiace per Taylor!!!)
veramente non esiste neanche una serie o una successione
che rappresenti anche discretamente (non continuamente)
la primitiva di e^(-x^2)?!?!?!?!?
Grazie in anticipo!!!!!! [;)]
Fury
volevo raccogliere tutte le informazioni possibili
sulla funzione ERF(x)! soprattutto su una sua possibile
approssimazione su tutto R (mi spiace per Taylor!!!)
veramente non esiste neanche una serie o una successione
che rappresenti anche discretamente (non continuamente)
la primitiva di e^(-x^2)?!?!?!?!?
Grazie in anticipo!!!!!! [;)]
Fury
Risposte
Come si è visto nel post precedente, la funzione erfc(x) = 1-erf(x) è assai meglio rappresentata su scala logaritmica che non su scala lineare e i motivi di ciò sono del tutto evidenti. Questa semplice considerazione indice quindi a cercare una approssimazione polinomiale ‘abbastanza accurata’ del logaritmo della funzione erfc(x) ottendo due sostanziali utili risultati…
a) grande semplificazione del calcolo
b) possibilità di valutare la funzione per valori di x ‘grandi’ [diciamo per x>5.5…], per il quali il calcolo diretto diviene probitivo a causa della precisione finita della macchina da calcolo utilizzata
Una soluzione standard a questo è dato dallo sviluppo in serie di Taylor di una funzione f(x), della quale si conoscono in un punto $x_0$ il valore della fuzione e di tutte le sue derivate…
$f(x)= f(x_0) + f^{\prime}(x_0)(x-x_0)/(1!) + f^((2))(x_0)(x-x_0)^2/(2!) + … + f^((n))(x_0) (x-x_0)^n/(n!) + …$ (1)
Nel nostro caso la funzione da svilippare è
$f(x)= ln [g(x)]$ (2)
... con…
$g(x)= erfc(x) = 1-2/sqrt(pi) int_0^x e^(-t^2) dt$ (3)
... nell’intorno di x=0. Un simile sviluppo è più noto come ‘serie di McLaurin’ e risulterà pertanto…
f(x)= sum_(n=0)^(+oo) a_n x^n$ (4)
… in cui…
$a_n= f^((n))(x_0)/(n!)$ (5)
Prima di iniziare ricordiamo che la derivata di ordine n della funzione g(x)=erfc(x) è…
$d^n/(dx^n) g(x) =-2/sqrt(pi) d^(n-1)/(dx^(n-1)) e^(-x^2)$ =
= $(-1)^n 2/sqrt(pi) e^(-x^2) * H_(n-1) (x)$ [n>0] (6)
in cui $H_(n)(x)$ è il polinomio di Hermite di grado n. Tra le proprietà dei polinomi di Hermite ci sarà utile la seguente…
$H_(2n-1) (0)=0$
$H_(2n)(0)=(-1)^n 2^n [1.3.5....(2n-1)]$ (7)
Sarà quindi…
$g(0)=1$
$g^(')(0) = -2/sqrt(pi) H_0(0) = -2/sqrt(pi)$
$g^((2))(0) = 2/sqrt(pi) H_1(0) =0$
$g^((3))(0) = -2/sqrt(pi) H_2(0) = 4/sqrt(pi)$
$g^((4))(0) = 2/sqrt(pi)*H_3(0) = 0$ (8)
Fatto questo procediamo al calcolo delle an che compaiono nella (4). Per n=0 sarà …
$a_0= ln [g(0)] = 0$
Per n=1 sarà…
$a_1= g^(')(0)/g(0)= -2/sqrt(pi) = -1.1283791671$
Per n=2 sarà…
$a_2= -g^(')(0)^2/(2!) = -2/pi= -.636619772368$
Per n=3 sarà…
$a3= [g^((3))(0)+2g^(')(0)^3]/(3!) = [4/sqrt(pi) –16/(pi^(3/2))]/(3!) = -.10277603302$
Per n=4 sarà…
$a_4= -4 [g^(')(0)*g^((3))(0)]/(4!) = [32/pi-96/(pi^2)]/(4!) = .019128447009$
Prima di procedere al calcolo dei termini successivi è bene osservare che risultati si ottengono troncando la serie al termine rispettivamente di grado due, tre e quattro…

Nel diagramma sono riportati…
a) il valore di log 10 [erfc(x)] calcolato con paziente applicazione della regola di Simpson [in nero…]
b) il valore di log 10 [erfc(x)] calcolato arrestando lo sviluppo in serie al termine di grado 2 [in rosso…]
c) il valore di log 10 [erfc(x)] calcolato arrestando lo sviluppo in serie al termine di grado 3 [in verde…]
d) il valore di log 10 [erfc(x)] calcolato arrestando lo sviluppo in serie al termine di grado 4 [in azzurro…]
Come logico aspettarsi la precisione cresce al crescere del grado. Per valori di x ‘grandi’ tuttavia è chiaro che la precisione diviene sempre più scarsa, a meno che non si voglia elevare il grado del polinomio oltre misura. Questo ‘difetto’ è tipico dello sviluppo in serie di Taylor, in cui quanto più ci si allontana dal punto xo [nel nostro caso x=0…], tanto più cresce l’errore. Diciamo che lo sviluppo di Taylor del quarto ordine dà risultati ottimi per valori di x non superiori a x=2.2 [erfc (2.2) circa uguale a $10^-3$…] dopo di che risultato è utile solo come stima preliminare ‘peggiorativa’. Abbiamo visto in precedenza però che per ottenere un risultato occorreva sommare venti termini, mentre qui ne bastano quattro e pertanto il metodo ora illustrato è pur sempre un miglioramento. Prossimamente esamineremo un approccio simile nel metodo ma che garantisce precisione assai maggiore…
cordiali saluti
lupo grigio

a) grande semplificazione del calcolo
b) possibilità di valutare la funzione per valori di x ‘grandi’ [diciamo per x>5.5…], per il quali il calcolo diretto diviene probitivo a causa della precisione finita della macchina da calcolo utilizzata
Una soluzione standard a questo è dato dallo sviluppo in serie di Taylor di una funzione f(x), della quale si conoscono in un punto $x_0$ il valore della fuzione e di tutte le sue derivate…
$f(x)= f(x_0) + f^{\prime}(x_0)(x-x_0)/(1!) + f^((2))(x_0)(x-x_0)^2/(2!) + … + f^((n))(x_0) (x-x_0)^n/(n!) + …$ (1)
Nel nostro caso la funzione da svilippare è
$f(x)= ln [g(x)]$ (2)
... con…
$g(x)= erfc(x) = 1-2/sqrt(pi) int_0^x e^(-t^2) dt$ (3)
... nell’intorno di x=0. Un simile sviluppo è più noto come ‘serie di McLaurin’ e risulterà pertanto…
f(x)= sum_(n=0)^(+oo) a_n x^n$ (4)
… in cui…
$a_n= f^((n))(x_0)/(n!)$ (5)
Prima di iniziare ricordiamo che la derivata di ordine n della funzione g(x)=erfc(x) è…
$d^n/(dx^n) g(x) =-2/sqrt(pi) d^(n-1)/(dx^(n-1)) e^(-x^2)$ =
= $(-1)^n 2/sqrt(pi) e^(-x^2) * H_(n-1) (x)$ [n>0] (6)
in cui $H_(n)(x)$ è il polinomio di Hermite di grado n. Tra le proprietà dei polinomi di Hermite ci sarà utile la seguente…
$H_(2n-1) (0)=0$
$H_(2n)(0)=(-1)^n 2^n [1.3.5....(2n-1)]$ (7)
Sarà quindi…
$g(0)=1$
$g^(')(0) = -2/sqrt(pi) H_0(0) = -2/sqrt(pi)$
$g^((2))(0) = 2/sqrt(pi) H_1(0) =0$
$g^((3))(0) = -2/sqrt(pi) H_2(0) = 4/sqrt(pi)$
$g^((4))(0) = 2/sqrt(pi)*H_3(0) = 0$ (8)
Fatto questo procediamo al calcolo delle an che compaiono nella (4). Per n=0 sarà …
$a_0= ln [g(0)] = 0$
Per n=1 sarà…
$a_1= g^(')(0)/g(0)= -2/sqrt(pi) = -1.1283791671$
Per n=2 sarà…
$a_2= -g^(')(0)^2/(2!) = -2/pi= -.636619772368$
Per n=3 sarà…
$a3= [g^((3))(0)+2g^(')(0)^3]/(3!) = [4/sqrt(pi) –16/(pi^(3/2))]/(3!) = -.10277603302$
Per n=4 sarà…
$a_4= -4 [g^(')(0)*g^((3))(0)]/(4!) = [32/pi-96/(pi^2)]/(4!) = .019128447009$
Prima di procedere al calcolo dei termini successivi è bene osservare che risultati si ottengono troncando la serie al termine rispettivamente di grado due, tre e quattro…

Nel diagramma sono riportati…
a) il valore di log 10 [erfc(x)] calcolato con paziente applicazione della regola di Simpson [in nero…]
b) il valore di log 10 [erfc(x)] calcolato arrestando lo sviluppo in serie al termine di grado 2 [in rosso…]
c) il valore di log 10 [erfc(x)] calcolato arrestando lo sviluppo in serie al termine di grado 3 [in verde…]
d) il valore di log 10 [erfc(x)] calcolato arrestando lo sviluppo in serie al termine di grado 4 [in azzurro…]
Come logico aspettarsi la precisione cresce al crescere del grado. Per valori di x ‘grandi’ tuttavia è chiaro che la precisione diviene sempre più scarsa, a meno che non si voglia elevare il grado del polinomio oltre misura. Questo ‘difetto’ è tipico dello sviluppo in serie di Taylor, in cui quanto più ci si allontana dal punto xo [nel nostro caso x=0…], tanto più cresce l’errore. Diciamo che lo sviluppo di Taylor del quarto ordine dà risultati ottimi per valori di x non superiori a x=2.2 [erfc (2.2) circa uguale a $10^-3$…] dopo di che risultato è utile solo come stima preliminare ‘peggiorativa’. Abbiamo visto in precedenza però che per ottenere un risultato occorreva sommare venti termini, mentre qui ne bastano quattro e pertanto il metodo ora illustrato è pur sempre un miglioramento. Prossimamente esamineremo un approccio simile nel metodo ma che garantisce precisione assai maggiore…
cordiali saluti
lupo grigio

Come ho già tentato di spiegare in precedenza, nella gran parte dei casi pratici, quello che interessa non è la funzione erf(x), bensì la sua complementare erfc(x)=1-erf(x) e il calcolo di quest’ultima per valori di x ‘grandi’ costituisce un problema niente affatto banale. Anni or sono, con la ‘paziente’ applicazione della regola di Simpson distribuita su di un gran numero di punti, ilò sottoscritto si è calcolato il valore di erfc(x) fino ad x=5 con precisione di 12 cifre. Il risultato di questo calcolo è illustrato nella figura seguente, nella quale è anche riportato un grafico del logaritmo della funzione [non ha molto senso reappresentare la funzione erfc(x) su scala lineare…]…
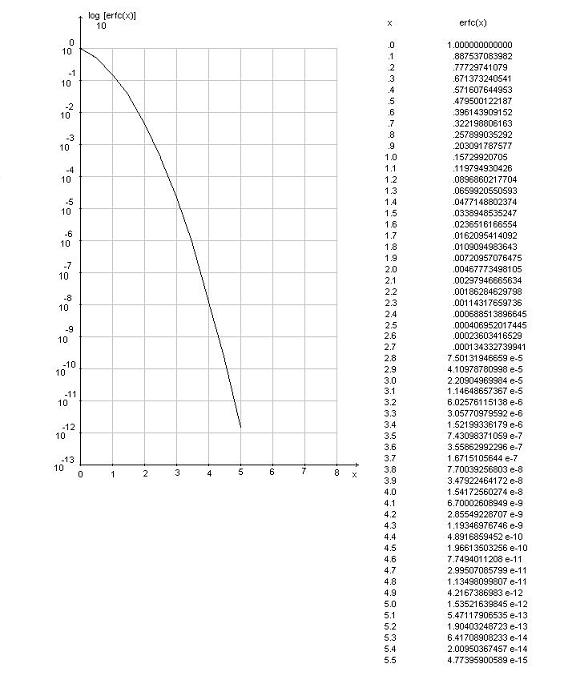
Nel caso sia necessario valutare la funzione per valori di x maggiori, una strada percorribile sarebbe quella di trovare una approssimazione polinomiale del logaritmo della funzione in modo da poterne ‘estrapolare’ i valori per valori di x superiori a 5. In un prossimo postato vedremo di affrontare questo problema…
cordiali saluti
lupo grigio


Nel caso sia necessario valutare la funzione per valori di x maggiori, una strada percorribile sarebbe quella di trovare una approssimazione polinomiale del logaritmo della funzione in modo da poterne ‘estrapolare’ i valori per valori di x superiori a 5. In un prossimo postato vedremo di affrontare questo problema…
cordiali saluti
lupo grigio

No, Camillo, cosa dici? mi hai frainteso, ho apprezzato molto! anche perchè io sapevo che
si poteva vare con mc laurin, ma non sapevo esprimerla con quella
serie! apprezzo sempre quando posso imparare qualcosa di nuovo! quello che volevo chiedere principalmente era se si conosce una
funzione che approssimi quasi perfettamente!
io ho provato a fugnare un po un'arctan(x), che le assomiglia molto, con
un'esponenziale con all'esponente la derivata prima di x^2 (esponente della gaussiana!).

si poteva vare con mc laurin, ma non sapevo esprimerla con quella
serie! apprezzo sempre quando posso imparare qualcosa di nuovo! quello che volevo chiedere principalmente era se si conosce una
funzione che approssimi quasi perfettamente!
io ho provato a fugnare un po un'arctan(x), che le assomiglia molto, con
un'esponenziale con all'esponente la derivata prima di x^2 (esponente della gaussiana!).

Per Fury : vedo che non hai apprezzato il mio modesto contributo : ma dimmi, come hai fatto a tirar fuori quella tua approssimazione ?
Camillo
Camillo
La ‘funzione errore’ e la sua ‘complementare’ sono asolutamente fondamentali nella teoria [e anche nella ‘pratica’…] dell’informatica e della comunicazione. Non stupisce pertanto che ad esse è stato dedicata una gran mole di studio fin dal XVII° secolo. La ‘funzione errore’ è definita come…
$erf(x) = 2/sqrt(pi) int_0^x e^(-t^2) dt$ (1)
… e la sua complementare come…
$erfc(x)= 1-erf(x)$ (2)
E’ importante notare che, dal punto di vista pratico, la (2) è quasi sempre più utile della (1), giacchè fornisce indicazione diretta del ‘tasso di errore’ di indeterminato processo. Non di rado per certi processi sono richiesti valori di tasso di errore non superiori a $10^(-12)$/$10^(-15)$ e questo la dice lunga sulla criticità del calcolo della funzione erf(x) per valori di x ‘abbastanza grandi’. L’approccio più semplice per il calcolo dell’integrale (1) è basato sullo sviluppo in serie della funzione $e^(-t^2)$…
$e^(-t^2) = sum_(n=0)^(+oo) (-1)^n * t^(2n)/(n!)$ (3)
... da cui, integrando termine a termine, si ottiene…
$erf(x) = 2/sqrt(pi) sum_(n=0)^(+oo) (-1)^n * x^(2n+1)/[(2n+1)*n!]$ (4)
In apparenza sembra che si possa nutrire un certo ottimismo in quanto si tratta di una serie a segni alterni ed è noto che, approssimando la (4) con la somma di un numero finito di termini, l’errore che si commette non supera [in valore assoluto] il primo termine trascurato. Per esempio quanti termini è necessario sommare per avere quattro decimali esatti?… Il termine n-esimo della serie (4) è, a parte il segno, …
$an = 2/sqrt(pi) * x^(2n+1)/[(2n+1)*n!]$ (5)
Imporre an<$10^(-4)$ equivale ad imporre…
$x^(2n+1)< ½ 10^(-4)sqrt(pi)(2n+1)n!$ (6)
Per x=1 si vede che è sufficiente sommare 8 termini per ottenere lo scopo. Se poniamo x=2 i termini da sommare divengono 15. Se poniamo x=2.5 i termini da sommare divengono 20. Per valori di x più elevati il numero di termini necessari cresce al punto tale da rendere l’accumulo degli errori di arrotondamento di entità paragonabile all’errore che si vuole ottenere, per cui il metodo in pratica non funziona più [provare per credere!…]. Prossimamente proveremo a trovare qualche altro sistema…
cordiali saluti
lupo grigio

$erf(x) = 2/sqrt(pi) int_0^x e^(-t^2) dt$ (1)
… e la sua complementare come…
$erfc(x)= 1-erf(x)$ (2)
E’ importante notare che, dal punto di vista pratico, la (2) è quasi sempre più utile della (1), giacchè fornisce indicazione diretta del ‘tasso di errore’ di indeterminato processo. Non di rado per certi processi sono richiesti valori di tasso di errore non superiori a $10^(-12)$/$10^(-15)$ e questo la dice lunga sulla criticità del calcolo della funzione erf(x) per valori di x ‘abbastanza grandi’. L’approccio più semplice per il calcolo dell’integrale (1) è basato sullo sviluppo in serie della funzione $e^(-t^2)$…
$e^(-t^2) = sum_(n=0)^(+oo) (-1)^n * t^(2n)/(n!)$ (3)
... da cui, integrando termine a termine, si ottiene…
$erf(x) = 2/sqrt(pi) sum_(n=0)^(+oo) (-1)^n * x^(2n+1)/[(2n+1)*n!]$ (4)
In apparenza sembra che si possa nutrire un certo ottimismo in quanto si tratta di una serie a segni alterni ed è noto che, approssimando la (4) con la somma di un numero finito di termini, l’errore che si commette non supera [in valore assoluto] il primo termine trascurato. Per esempio quanti termini è necessario sommare per avere quattro decimali esatti?… Il termine n-esimo della serie (4) è, a parte il segno, …
$an = 2/sqrt(pi) * x^(2n+1)/[(2n+1)*n!]$ (5)
Imporre an<$10^(-4)$ equivale ad imporre…
$x^(2n+1)< ½ 10^(-4)sqrt(pi)(2n+1)n!$ (6)
Per x=1 si vede che è sufficiente sommare 8 termini per ottenere lo scopo. Se poniamo x=2 i termini da sommare divengono 15. Se poniamo x=2.5 i termini da sommare divengono 20. Per valori di x più elevati il numero di termini necessari cresce al punto tale da rendere l’accumulo degli errori di arrotondamento di entità paragonabile all’errore che si vuole ottenere, per cui il metodo in pratica non funziona più [provare per credere!…]. Prossimamente proveremo a trovare qualche altro sistema…
cordiali saluti
lupo grigio

Penso che sui libri di statistica si faccia un'approssimazione integrando numericamente le gaussiane: in questo modo si puo' avere una precisione buona quanto si vuole.
Questa la sapevo anch'io! io dicevo un'approssimazione
per fini pratici! guarda in questo link: http://www.hal.varese.it/~bernasconi/pdf/nsan12.pdf
a pagina 4 si dice che in archeoastronomia viene usata
un'altra funzione, che però discosta da erf(x) di un errore molto
notevole! io sono riuscito a trovare un'approssimazione
con un errore più piccolo ( 0.03401471297 ).
guarda il confronto!
(la funzione erf(x) è quella rossa)
ERF(x) vs ARCHEOASTRONOMIA

ERF(x) vs MIA APPROSSIMAZIONE


per fini pratici! guarda in questo link: http://www.hal.varese.it/~bernasconi/pdf/nsan12.pdf
a pagina 4 si dice che in archeoastronomia viene usata
un'altra funzione, che però discosta da erf(x) di un errore molto
notevole! io sono riuscito a trovare un'approssimazione
con un errore più piccolo ( 0.03401471297 ).
guarda il confronto!
(la funzione erf(x) è quella rossa)
ERF(x) vs ARCHEOASTRONOMIA

ERF(x) vs MIA APPROSSIMAZIONE


La funzione erf(z) normalizzata è definita come:
(2/sqrt(pi)) *integrale tra 0 e z di(e^(-t^2)*dt) e può essere rappresentata dallo sviluppo di Mc Laurin:
erf(z) = (2/sqrt(pi))*(somma per n da 0 a inf) di : [((-1)^n)*z^(2n+1)]/[n!*(2n+1)] = (2/sqrt(pi))*[z-z^3/3+z^5/10-z^7/42+......]
che corrisponde a quello che dice david_e : infatti integrando termine a termine lo sviluppoo di Mclaurin di e^(-z^2) si ottiene proprio lo sviluppo sopra indicato.
Vai a vedere qui :
http://mathworld.wolfram.com/Erf.html
Camillo
(2/sqrt(pi)) *integrale tra 0 e z di(e^(-t^2)*dt) e può essere rappresentata dallo sviluppo di Mc Laurin:
erf(z) = (2/sqrt(pi))*(somma per n da 0 a inf) di : [((-1)^n)*z^(2n+1)]/[n!*(2n+1)] = (2/sqrt(pi))*[z-z^3/3+z^5/10-z^7/42+......]
che corrisponde a quello che dice david_e : infatti integrando termine a termine lo sviluppoo di Mclaurin di e^(-z^2) si ottiene proprio lo sviluppo sopra indicato.
Vai a vedere qui :
http://mathworld.wolfram.com/Erf.html
Camillo
ma, sapete che funzione si usa generalmente per approssimare i
valori di erf(x)?

valori di erf(x)?

Scusa ma se e(-x^2) e' analitica (ovvero e' uguale su tutto R al limite della sua serie di Taylor), a maggiore ragione lo sara' la sua primitiva!
Poi DEVE esistere per forza una serie che approssima una funzione integrale: l'integrale di Riemann e anche quello di Lebesgue sono definiti a partire da somme di cui si cerca l'inf e il sup! Se l'integrale esiste vuol dire che e' uguale all'inf delle somme superiori e al sup delle somme superiori.
Poi DEVE esistere per forza una serie che approssima una funzione integrale: l'integrale di Riemann e anche quello di Lebesgue sono definiti a partire da somme di cui si cerca l'inf e il sup! Se l'integrale esiste vuol dire che e' uguale all'inf delle somme superiori e al sup delle somme superiori.
Se cerchi su qualche raccolta di primitive, troverai sicuramente alcune serie che la approssimano.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo