Cronoconnettività
"Cominceremo se i tempi tecnici lo consentiranno, a pubblicare gli appunti, e i teoremi di un matematico di orgini messinesi, morto all' età di 39 anni suicida . i cui risultati ci sono perventuti da un amico comune.
[img]http://1.bp.blogspot.com/-2nqamg1_gnQ/T9nqVS0TTYI/AAAAAAAAACQ/wBiQ_GUcMsw/s1600/foto+giuseppe.bmp[/img]
Giuseppe Albanese.
Ogni risultato sarà postato.
Oltre a questo, probabilmente i post dedicati alle scienze, aumenteranno con qualche contributo di un fisico del cnr, sulle energie rinnovabili e sulle esperienze connesse.
Cain. kiss. "
Con questo mess. Cominciamo a pubblicare gli appunti di un matematico scomparso il sito del blog è:
http://cronoconnettivita.blogspot.it/
Per leggere gli appunti o i racconti, cliccare su buona lettura e si aprirà un link da cui scaricare.
Il blog si occupa in generale di tutto ciò che di solito potrebbe essere convenzionalmente scomodo pubblicare poiché interessa, solo determinate fasce, minori.
Mi riferisco, sia alla matematica,che ai racconti(fantascienza, steam punk etc..), ma anche alle recensioni.
Se qualcuno ha un risultato che vorrebbe rendere noto, o scrivere un articolo su un problema o una teoria, pubblicare una recensione di un libro anche vecchio, o un racconto che tiene nel cassetto, noi se la cosa è convincente lo metteremo in rete.
Grazie per il tempo che vi ho rubato, spero che qualcosa in mezzo al caos possa interessarvi o stimolarvi a riflettere. BYE
[img]http://1.bp.blogspot.com/-2nqamg1_gnQ/T9nqVS0TTYI/AAAAAAAAACQ/wBiQ_GUcMsw/s1600/foto+giuseppe.bmp[/img]
Giuseppe Albanese.
Ogni risultato sarà postato.
Oltre a questo, probabilmente i post dedicati alle scienze, aumenteranno con qualche contributo di un fisico del cnr, sulle energie rinnovabili e sulle esperienze connesse.
Cain. kiss. "
Con questo mess. Cominciamo a pubblicare gli appunti di un matematico scomparso il sito del blog è:
http://cronoconnettivita.blogspot.it/
Per leggere gli appunti o i racconti, cliccare su buona lettura e si aprirà un link da cui scaricare.
Il blog si occupa in generale di tutto ciò che di solito potrebbe essere convenzionalmente scomodo pubblicare poiché interessa, solo determinate fasce, minori.
Mi riferisco, sia alla matematica,che ai racconti(fantascienza, steam punk etc..), ma anche alle recensioni.
Se qualcuno ha un risultato che vorrebbe rendere noto, o scrivere un articolo su un problema o una teoria, pubblicare una recensione di un libro anche vecchio, o un racconto che tiene nel cassetto, noi se la cosa è convincente lo metteremo in rete.
Grazie per il tempo che vi ho rubato, spero che qualcosa in mezzo al caos possa interessarvi o stimolarvi a riflettere. BYE
Risposte
cosa che sono uguali i punti? E si la prima...
cmq, tornando a noi non è ovvio. due punti che si susseguono e che formano un angolo, nel cerchio maggiore diventano un intervallo sempre finito n.
Quindi scusa cosa c'è di ovvio? a me sembra molto incoerente piuttosto...
cmq, tornando a noi non è ovvio. due punti che si susseguono e che formano un angolo, nel cerchio maggiore diventano un intervallo sempre finito n.
Quindi scusa cosa c'è di ovvio? a me sembra molto incoerente piuttosto...
"Icarocremisi":
ora che ho attirato un po di attenzione. Possiamo cominciare, scusami luca, non volevo dire che le tue appendici sono unidimensionali. se questo può valere qualcosa nell' averti in parte usato:
Paradosso del cerchio:
Il paradosso consiste, semplicemente nel fatto che se costruisco due cerchi, uno inscritto nell' altro ed estendo un raggio dal centro ( che faccio ruotare e che unisce, entrambi i cerchi come in figura, per ogni punto nel cerchio più piccolo ne esiste uno sul cerchio più grande. (non credo ci voglia 190 di qi per comprenderlo ma se qualcuno ha dei problemi, posso essere più dettagliato.
È la prima frase che scrivi che abbia un senso matematico, anche se di paradosso ha ben poco. Mi sembra tutto piuttosto ovvio.
Passiamo al resto? Palla Piena? tridimensionale. e non è esattamente un punto secondo euclide. O forse è solo più una traccia la geometria euclida, più che una certezza?
Quando siete pronti, ditemelo e passiamo oltre. Per me è piuttosto banale.
Ps luca io non ho mai vita facile mi sono subito abituato però.
Quando siete pronti, ditemelo e passiamo oltre. Per me è piuttosto banale.
Ps luca io non ho mai vita facile mi sono subito abituato però.
Dimostrazione dell' impossibilita che l' insieme dei punti che compongono i due perimetri abbiano medesima cardinalità.
Parole povere, il numero degli elementi è impossibile che sia uguale.
1) passaggio, prendiamo la costruzione precedente e disegnamo un altro raggio che passi per un intorno del punto segnato dalle intersezioni fra il raggio prolungato e i due perimetri in modo da formare un angolo:[img]
http://3.bp.blogspot.com/-XJqWMLuTWi0/T ... erchio.png[/img]
Ora i due raggi, che partono dal medesimo punto e attraversano i due punti uno accanto all' altro nel primo cerchio, nel secondo a distanza n, dato che formano un angolo che si distanzia, devono toccare due punti, ma in un intervallo maggiore.
Ovviamente saranno 3 o 4, o 6 in tutto i punti che formano la parte di perimetro del secondo cerchio, limitati dall' angolo.
Traccio da questi punti che non vengono toccati tutti i raggi, che li congiungono al centro del primo cerchio( e anche del secondo).
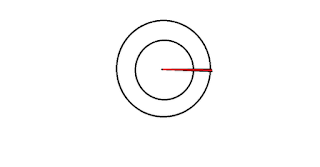
Questo implica che tutti i raggi, del primo cerchio corrispondenti ad almeno un punto, non bastano a toccare ogni punto del secondo cerchio.
Ovviamente basta immaginare tutti gli angoli formati da punti continui del perimetro del primo cerchio e tutti quelli invece che formano il secondo.
E con questo il paradosso è accantonato per sempre.
2) Ma se i segmenti sono unidimensionali, cioè non hanno spessore, questa che io chiamo sovrapposizione di stati, cosa comporta?
Che il segmento deve avere uno spessore, prossimo allo zero ma deve averlo. Quindi il punto (usato come unità di misura).. del segmento che forma il raggio ha uno spessore, non può essere in alcun modo unidimensionale.
A me non pare complicato.
Se non si capisce posso spiegarlo nessun problema. Anche se così mi sembra di imboccare un bambino. con l' ultimo post se volete vi indico anche il mio di qi, e il tempo che ho impiegato a finire tutti i test.
Se volete possiamo sollevare cantor e hilbert e analizzare il tutto secondo un' altra prospettiva-
Parole povere, il numero degli elementi è impossibile che sia uguale.
1) passaggio, prendiamo la costruzione precedente e disegnamo un altro raggio che passi per un intorno del punto segnato dalle intersezioni fra il raggio prolungato e i due perimetri in modo da formare un angolo:[img]
http://3.bp.blogspot.com/-XJqWMLuTWi0/T ... erchio.png[/img]
Ora i due raggi, che partono dal medesimo punto e attraversano i due punti uno accanto all' altro nel primo cerchio, nel secondo a distanza n, dato che formano un angolo che si distanzia, devono toccare due punti, ma in un intervallo maggiore.
Ovviamente saranno 3 o 4, o 6 in tutto i punti che formano la parte di perimetro del secondo cerchio, limitati dall' angolo.
Traccio da questi punti che non vengono toccati tutti i raggi, che li congiungono al centro del primo cerchio( e anche del secondo).

Questo implica che tutti i raggi, del primo cerchio corrispondenti ad almeno un punto, non bastano a toccare ogni punto del secondo cerchio.
Ovviamente basta immaginare tutti gli angoli formati da punti continui del perimetro del primo cerchio e tutti quelli invece che formano il secondo.
E con questo il paradosso è accantonato per sempre.
2) Ma se i segmenti sono unidimensionali, cioè non hanno spessore, questa che io chiamo sovrapposizione di stati, cosa comporta?
Che il segmento deve avere uno spessore, prossimo allo zero ma deve averlo. Quindi il punto (usato come unità di misura).. del segmento che forma il raggio ha uno spessore, non può essere in alcun modo unidimensionale.
A me non pare complicato.
Se non si capisce posso spiegarlo nessun problema. Anche se così mi sembra di imboccare un bambino. con l' ultimo post se volete vi indico anche il mio di qi, e il tempo che ho impiegato a finire tutti i test.
Se volete possiamo sollevare cantor e hilbert e analizzare il tutto secondo un' altra prospettiva-
ora che ho attirato un po di attenzione. Possiamo cominciare, scusami luca, non volevo dire che le tue appendici sono unidimensionali. se questo può valere qualcosa nell' averti in parte usato:
Paradosso del cerchio:
Il paradosso consiste, semplicemente nel fatto che se costruisco due cerchi, uno inscritto nell' altro ed estendo un raggio dal centro ( che faccio ruotare e che unisce, entrambi i cerchi come in figura, per ogni punto nel cerchio più piccolo ne esiste uno sul cerchio più grande. (non credo ci voglia 190 di qi per comprenderlo ma se qualcuno ha dei problemi, posso essere più dettagliato.
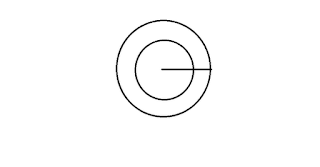
Paradosso del cerchio:
Il paradosso consiste, semplicemente nel fatto che se costruisco due cerchi, uno inscritto nell' altro ed estendo un raggio dal centro ( che faccio ruotare e che unisce, entrambi i cerchi come in figura, per ogni punto nel cerchio più piccolo ne esiste uno sul cerchio più grande. (non credo ci voglia 190 di qi per comprenderlo ma se qualcuno ha dei problemi, posso essere più dettagliato.

Sono d'accordo con Luca Lussardi, un programma del computer che generi frasi matematiche a caso comporrebbe un testo di maggiore senso. Capiamoci, non è che sia incredulo di ciò che dimostri, è proprio che non ho capito neanche lontanamente COSA stai dimostrando. Penso non ci sia neanche un frase nelle prime 3-4 pagine in cui ogni parola abbia il suo usuale senso matematico. Ne tanto meno ho trovato che i disegni aiutassero molto. In pratica il tuo testo mi risulta come un agglomerato di parole matematiche (elementari) messe a caso. Ti assicuro che le definizioni sono la parte fondamentale della matematica.
Che cosa significhi poi che un punto abbia 2 dimensioni proprio mi sfugge. Inoltre se proprio vuoi potresti quasi dire che ne contiene infinite dato che ogni palla "piena" n-dimensionale può essere contratta in un punto, e questo in alcuni casi vuol dire che tu puoi considerare le due cose come sostanzialmente equivalenti (anche se in genere non lo sono affatto).
Che cosa significhi poi che un punto abbia 2 dimensioni proprio mi sfugge. Inoltre se proprio vuoi potresti quasi dire che ne contiene infinite dato che ogni palla "piena" n-dimensionale può essere contratta in un punto, e questo in alcuni casi vuol dire che tu puoi considerare le due cose come sostanzialmente equivalenti (anche se in genere non lo sono affatto).
Benissimo, allora andiamo avanti: per tutto quello che dirò mi riferisco al pdf intitolato "bidimensionalità del punto".
"Costruiamo sul piano una figura a curvatura minore di 2"
cosà è la curvatura di una figura? Niente viene detto e si disegnano solo quadrati poi... figure molto curve.
"Le diagonali, indicano chiaramente come è impossibile costruire un quadrato che non abbia una parte più interna > del segmento."
Non vuol dire niente.
"Il punto diagonale, deve necessariamente esistere. Se non esistesse il quadrato non potrebbe essere perfetto."
??????? cosa è il punto diagonale? Come è definito un quadrato perfetto?
"Ipotizziamo che il punto nell' angolo non sia frutto di due dimensioni. Quindi se non appartiene ne' a destra né a sinistra non esiste. E' solo frutto di una congiunzione di due segmenti unidimensionali. La sua continuità è dunque unidimensionale."
Cosa vuol dire che un punto è frutto di due dimensioni? cosa vuol dire che appartiene a destra o a sinistra? continuità unidimensionale?
Devo andare avanti? Ti rinnovo l'invito: lascia perdere o avrai vita breve qui da noi; oppure studia prima e ripresentati poi.
"Costruiamo sul piano una figura a curvatura minore di 2"
cosà è la curvatura di una figura? Niente viene detto e si disegnano solo quadrati poi... figure molto curve.
"Le diagonali, indicano chiaramente come è impossibile costruire un quadrato che non abbia una parte più interna > del segmento."
Non vuol dire niente.
"Il punto diagonale, deve necessariamente esistere. Se non esistesse il quadrato non potrebbe essere perfetto."
??????? cosa è il punto diagonale? Come è definito un quadrato perfetto?
"Ipotizziamo che il punto nell' angolo non sia frutto di due dimensioni. Quindi se non appartiene ne' a destra né a sinistra non esiste. E' solo frutto di una congiunzione di due segmenti unidimensionali. La sua continuità è dunque unidimensionale."
Cosa vuol dire che un punto è frutto di due dimensioni? cosa vuol dire che appartiene a destra o a sinistra? continuità unidimensionale?
Devo andare avanti? Ti rinnovo l'invito: lascia perdere o avrai vita breve qui da noi; oppure studia prima e ripresentati poi.
E con questo post. Spero di essere chiaro il più possibile.
1) quando si mettono in dubbio verità matematiche.
(e riguardo il post precedente e la risposta sull' unidimensionalità. E' un mero dato di fatto contrariamente a quello che diceva il ragazzo prima, che l' unidimensionalità del segmento astrattamente è costruibile, tanto come possono esistere astrattamente piani n dimensionali. Fortunatamente la ragione e la fantasia hanno pochi limiti)
Che non sempre saremo d'accordo, e che la forma non sempre può rispecchiare quelli che sono i nostri gusti o ciò che noi assumiamo che sia la forma corretta.
Ma questo non significa che non siano vere coerenti o non coerenti. Dato che è il dubbio l' animo della verità.
2) non c'è l' intenzione di offendere nessuno, e se qualcuno si riterrà offeso da qualcosa si chieda prima in che toni si è rivolto all' interlocutore. Sono idee in forma di appunti e come tali devono essere concepite. Avrei potuto portare questo ad altri e trovare una forma più perfetta che non aggiunge e non toglie nulla.
3) Io sono convinto della correttezza di quanto posto e posterò e lo faccio nella piena consapevolezza che questo potrebbe non essere compreso. Ma se non lo farei io, qualcun' altro lo farebbe prima o poi spero. E nessuno qui vuole convencere nessuno, se qualcuno sarà concorde, sarà perché lo ha constatato grazie al proprio ragionamento.
4) Lo scopo è proprio quello di aprirsi, ad idee nuove e persone nuove. E dare la possibilità di esprimersi attraverso canali non istituzionali.
5) ho detto che questo è il minore dei risultati ed è vero. E se già viene accettato così non vedo l'ora di postare gli altri.
Credo che dalle dinamiche del caos e del confronto sereno possano nascere cose interessanti ed è a questo che ambisco.
Per cui se qualcun altro, vorrà discuterne nessun problema. Ansi se i rapporti saranno civili. Di certo non ho da perdere.
Se l' intenzione è fare polemica sterile o dire assurdità. Io per primo mi riterrò offeso anche se ciò accadrà ad un interlocutore, che ha idee opposte alle mie.
Questo è uno spazio libero, lo scopo è approfittarsene e non autocastrarsi, privandoci di dire qualcosa perché questo urta qualcun altro.
E lo spazio che ho creato sul web idem. Malgrado lo screzio, sono sempre disposto ad ospitare qualsiasi idea purché sia coerente.
Ed è proprio questo il "punto" le idee devono avere il requisito della coerenza. Se non lo sono non sono esatte, o sono esatte solo seguendo determinati assiomi.
L' invito resta aperto.
1) quando si mettono in dubbio verità matematiche.
(e riguardo il post precedente e la risposta sull' unidimensionalità. E' un mero dato di fatto contrariamente a quello che diceva il ragazzo prima, che l' unidimensionalità del segmento astrattamente è costruibile, tanto come possono esistere astrattamente piani n dimensionali. Fortunatamente la ragione e la fantasia hanno pochi limiti)
Che non sempre saremo d'accordo, e che la forma non sempre può rispecchiare quelli che sono i nostri gusti o ciò che noi assumiamo che sia la forma corretta.
Ma questo non significa che non siano vere coerenti o non coerenti. Dato che è il dubbio l' animo della verità.
2) non c'è l' intenzione di offendere nessuno, e se qualcuno si riterrà offeso da qualcosa si chieda prima in che toni si è rivolto all' interlocutore. Sono idee in forma di appunti e come tali devono essere concepite. Avrei potuto portare questo ad altri e trovare una forma più perfetta che non aggiunge e non toglie nulla.
3) Io sono convinto della correttezza di quanto posto e posterò e lo faccio nella piena consapevolezza che questo potrebbe non essere compreso. Ma se non lo farei io, qualcun' altro lo farebbe prima o poi spero. E nessuno qui vuole convencere nessuno, se qualcuno sarà concorde, sarà perché lo ha constatato grazie al proprio ragionamento.
4) Lo scopo è proprio quello di aprirsi, ad idee nuove e persone nuove. E dare la possibilità di esprimersi attraverso canali non istituzionali.
5) ho detto che questo è il minore dei risultati ed è vero. E se già viene accettato così non vedo l'ora di postare gli altri.
Credo che dalle dinamiche del caos e del confronto sereno possano nascere cose interessanti ed è a questo che ambisco.
Per cui se qualcun altro, vorrà discuterne nessun problema. Ansi se i rapporti saranno civili. Di certo non ho da perdere.
Se l' intenzione è fare polemica sterile o dire assurdità. Io per primo mi riterrò offeso anche se ciò accadrà ad un interlocutore, che ha idee opposte alle mie.
Questo è uno spazio libero, lo scopo è approfittarsene e non autocastrarsi, privandoci di dire qualcosa perché questo urta qualcun altro.
E lo spazio che ho creato sul web idem. Malgrado lo screzio, sono sempre disposto ad ospitare qualsiasi idea purché sia coerente.
Ed è proprio questo il "punto" le idee devono avere il requisito della coerenza. Se non lo sono non sono esatte, o sono esatte solo seguendo determinati assiomi.
L' invito resta aperto.
se non leggi quello che non ti sembra corretto come ti possono convincere.. Oppure sei capace di autoconvincerti da solo?
inoltre:
Di certo da te potrei imparare qualcosa, tu sai anche quello che non leggi.
E cmq, non hai risposto....
Anche perché 1) umile non sei. 2) nessuno ti vuole convincere è un mero dato di fatto.
3) io studio quello che non so.
Per il resto scusa ma mi fai anche un pò ridere, sei piuttosto superbo... Complesso del pene?
Nessuno mi ha ancora convinto del contrario.
inoltre:
E io direi che se fossi serio dovresti prima studiarti la matematica con umiltà e poi affrontare le relative discussioni
Di certo da te potrei imparare qualcosa, tu sai anche quello che non leggi.
E cmq, non hai risposto....
Anche perché 1) umile non sei. 2) nessuno ti vuole convincere è un mero dato di fatto.
3) io studio quello che non so.
Per il resto scusa ma mi fai anche un pò ridere, sei piuttosto superbo... Complesso del pene?
"Icarocremisi":
Vedi se fosse come dici tu, i punti del cerchio sarebbero uguali, ma non è così.
Nessuno mi ha ancora convinto del contrario.
"Icarocremisi":
Io direi che se sei serio dovresti porre delle risposte precise
E io direi che se fossi serio dovresti prima studiarti la matematica con umiltà e poi affrontare le relative discussioni.
"Icarocremisi":
Sul piano bidimensionale, ogni linearità ruotando la base ortonormale di n gradi cessa di poter essere espressa in maniera solo lineareo meglio di poter essere espressa tramite una unica coordinata. Daltronde Euclide, lo ha dato come assioma.
Vai a leggerti gli Elementi di Euclide, poi ne riparliamo, ammesso sai cosa siano.
"Icarocremisi":
Ma non esistono nella realtà, segmenti privi di spessore né puoi costruirli.
E questa è la ciliegina sulla torta: che nella realtà oggetti puramente uni-dimensionali non esistono. Come dicono i bresciani: "è arrivato Marconi con la radio in mano".
In bocca al lupo per il proseguimento delle tue disquisizioni qui sul forum; per quanto mi riguarda ho già sentito abbastanza.
Vedi se fosse come dici tu, i punti del cerchio sarebbero uguali, ma non è così.
Se costruisci un cerchio esterno e parti dal presupposto che passano per l' intorno di due punti due segmenti che formano un angolo, ovviamente, nel cerchio esterno maggioe(immaginiamo un orologio), i segmenti che passano per i due punti se formano un angolo devono allargarsi, avrai n punti che non possono essere toccati, se tracci i segmenti, di questi n punti ti troverai ad avere raggi sovrapposti, ma se sono unidimensionali come puoi sovrapporli dato che non hanno spessore?
Io direi che se sei serio dovresti porre delle risposte precise, se no astieniti, daltronde nessuno ti obbliga a leggerlo. E se non ti piace e non lo condividi, puoi benissimo non leggerlo. Le posizioni qualunquiste non mi interessano perché non sono serie di per se. E la cosa è ovvia. Sul piano bidimensionale, ogni linearità ruotando la base ortonormale di n gradi cessa di poter essere espressa in maniera solo lineareo meglio di poter essere espressa tramite una unica coordinata. Daltronde Euclide, lo ha dato come assioma. Ma non esistono nella realtà, segmenti privi di spessore né puoi costruirli. Direi che a questo punto data la tua bravura e serietà ci darai la dimostrabilità del concetto che al momento a me sfugge. Prego... Sono curioso. Vediamo queste stringhe-
Ps e per dirla tutta, se non hai letto che giudichi? quello che pensi che sia?
Se costruisci un cerchio esterno e parti dal presupposto che passano per l' intorno di due punti due segmenti che formano un angolo, ovviamente, nel cerchio esterno maggioe(immaginiamo un orologio), i segmenti che passano per i due punti se formano un angolo devono allargarsi, avrai n punti che non possono essere toccati, se tracci i segmenti, di questi n punti ti troverai ad avere raggi sovrapposti, ma se sono unidimensionali come puoi sovrapporli dato che non hanno spessore?
Io direi che se sei serio dovresti porre delle risposte precise, se no astieniti, daltronde nessuno ti obbliga a leggerlo. E se non ti piace e non lo condividi, puoi benissimo non leggerlo. Le posizioni qualunquiste non mi interessano perché non sono serie di per se. E la cosa è ovvia. Sul piano bidimensionale, ogni linearità ruotando la base ortonormale di n gradi cessa di poter essere espressa in maniera solo lineareo meglio di poter essere espressa tramite una unica coordinata. Daltronde Euclide, lo ha dato come assioma. Ma non esistono nella realtà, segmenti privi di spessore né puoi costruirli. Direi che a questo punto data la tua bravura e serietà ci darai la dimostrabilità del concetto che al momento a me sfugge. Prego... Sono curioso. Vediamo queste stringhe-
Ps e per dirla tutta, se non hai letto che giudichi? quello che pensi che sia?
Per favore... questo è un forum di matematica serio. Solo se mi troverò a leggere cose serie avrete una mia partecipazione. Mi è bastato leggere le prime righe del paragrafo sulla bidimensionalità per interrompere la lettura.
pubblicazioni di appunti, hanno una forma molto libera.
1) la soluzione (viene definita, come il sottoinsieme di tutti i segmenti orizzontali e verticali che non tornano indietro e che congiunge entrata ad uscita)
2) Teorema se uscita ed entrata per ogni soluzione sono le medesime, le soluzioni sono o solo pari o solo dispari, ad esclusione di due soli casi punto centrale e diagonale.
3) questo implica che basta calcolare il coefficente angolare nel qual caso sono solo 4 angoli di 90°. Per comprendere se il segmento è una soluzione possibile o meno.
4) Se altero lo spazio e prendo in cosiderazione i punti interni la soluzione unica o le soluzioni uniche hanno due angoli, quindi prima gli dai l' orizzontale, e elimini i verticali, poi il verticale ed elimini gli orizzontali.
Ciò che resta è solo la soluzione.
Punto bidimensionale (sul piano esiste necessariamente, vedi l' allegato) se esiste almeno un punto del quadrato appartiene sia alla lunghezza che alla altezza, ma questo è ininfluente, per me quasi banale, il punto è che i punti diagonali dell' algoritmo del labirinto corrispondono, a situazioni tali dunque è indifferente se andare dritto o a destra e a sinistra. Serviva solo a questo credo.
Zenone, se i raggi che noi crediamo unidimensionali, si accavallano in posizione di stato, il paradosso del cerchio non esiste(il paradosso del cerchio indica che ogni cerchio a prescindere dalle dimensioni, illimitato abbia sempre lo stesso numero di punti), la conclusione è inoltre che sul piano bidimensionale la sola unidimensionalità non è coerente.
Seconda conclusione sui paradossi di zenone, se gli illimitati sono proporzionali tali che una parte di tutti gli N:
xN, può contenerli e inoltre creare spazi che non sono toccati dai raggi dei cerchi proporzionalmente più piccoli, 1) Achille raggiungerà la tartaruga, ed infine la conclusione più sconvolgente è che rispetto a v=s/t, se il tempo si riduce a 0, la velocità è infinita.
Cioè un paradosso in sintesi perché se il tempo diventa nullo o meglio la sua costante più piccola prossima allo 0, dovrebbe esistere la stasi.
Personalmente ne ho tratta un' altra idea, anche come conseguenza ma non è matura.
Martino discutendone, mi ha detto che esistono anche altri algoritmi riguardo i labirinti, io ne ho visti un paio in rete.
Ma nessuuno esclude costi di computazione. In pratica sapendo angolo di inizio e angolo della fine soltanto, di un percorso a segmenti orizzontali e verticali, tu non sai quale dei due sia pari o dispari, con il teorema invece non devi contare lo spazio o tornare indietro, lo sai e basta.
sai sempre se è pari o dispari a prescinderne dal numero e dalla lunghezza. In pratica ti basta sapere che se la soluzione è pari e non devi contarla, i percorsi dispari non sono soluzioni... etc..
Spero da neofita di essere stato chiaro.
Mi trovi concorde, la bellezza della matematica è nella sua libertà.
Scusa se non mi soffermo ma non ne ho il tempo al momento.
Se la tua domanda invece si riferisce al blog. E' nato come esperimento, per aprire uno spazio virtuale, dove far entrare idee di persone che solitamente non avrebbero grossi spazi. Se tu hai un racconto o vuoi scrivere un articolo o hai un' idea.
Scrivi alla mail e vedremo come fare e se possiamo aiutarti a esprimerla indipendentemente nel nostro spazio sul blog.
Almeno su 15 persone che hanno visto il post, qualcuno che si è incuriosito c'è. E sono contento che porti nel mess. una frase così bella. Grazie.
E cmq questo è il materiale meno importante, difatti è stato scelto come primo post.
Sicuramente dovrò aggiungerne un altro per indicare i paradossi di zenone e del cerchio, ma questo è poco importante il tempo c'è... e poi nulla esclude che qualcuno voglia avventurarsi da solo in rete, ansi se avete altre idee sui labirinti e ricordo che è affine ad un altro problema (del millenio) anche se non uguale, e cioè capire la strada più breve senza costi di computazione, scrivete non aspettiamo altro.
1) la soluzione (viene definita, come il sottoinsieme di tutti i segmenti orizzontali e verticali che non tornano indietro e che congiunge entrata ad uscita)
2) Teorema se uscita ed entrata per ogni soluzione sono le medesime, le soluzioni sono o solo pari o solo dispari, ad esclusione di due soli casi punto centrale e diagonale.
3) questo implica che basta calcolare il coefficente angolare nel qual caso sono solo 4 angoli di 90°. Per comprendere se il segmento è una soluzione possibile o meno.
4) Se altero lo spazio e prendo in cosiderazione i punti interni la soluzione unica o le soluzioni uniche hanno due angoli, quindi prima gli dai l' orizzontale, e elimini i verticali, poi il verticale ed elimini gli orizzontali.
Ciò che resta è solo la soluzione.
Punto bidimensionale (sul piano esiste necessariamente, vedi l' allegato) se esiste almeno un punto del quadrato appartiene sia alla lunghezza che alla altezza, ma questo è ininfluente, per me quasi banale, il punto è che i punti diagonali dell' algoritmo del labirinto corrispondono, a situazioni tali dunque è indifferente se andare dritto o a destra e a sinistra. Serviva solo a questo credo.
Zenone, se i raggi che noi crediamo unidimensionali, si accavallano in posizione di stato, il paradosso del cerchio non esiste(il paradosso del cerchio indica che ogni cerchio a prescindere dalle dimensioni, illimitato abbia sempre lo stesso numero di punti), la conclusione è inoltre che sul piano bidimensionale la sola unidimensionalità non è coerente.
Seconda conclusione sui paradossi di zenone, se gli illimitati sono proporzionali tali che una parte di tutti gli N:
xN, può contenerli e inoltre creare spazi che non sono toccati dai raggi dei cerchi proporzionalmente più piccoli, 1) Achille raggiungerà la tartaruga, ed infine la conclusione più sconvolgente è che rispetto a v=s/t, se il tempo si riduce a 0, la velocità è infinita.
Cioè un paradosso in sintesi perché se il tempo diventa nullo o meglio la sua costante più piccola prossima allo 0, dovrebbe esistere la stasi.
Personalmente ne ho tratta un' altra idea, anche come conseguenza ma non è matura.
Martino discutendone, mi ha detto che esistono anche altri algoritmi riguardo i labirinti, io ne ho visti un paio in rete.
Ma nessuuno esclude costi di computazione. In pratica sapendo angolo di inizio e angolo della fine soltanto, di un percorso a segmenti orizzontali e verticali, tu non sai quale dei due sia pari o dispari, con il teorema invece non devi contare lo spazio o tornare indietro, lo sai e basta.
sai sempre se è pari o dispari a prescinderne dal numero e dalla lunghezza. In pratica ti basta sapere che se la soluzione è pari e non devi contarla, i percorsi dispari non sono soluzioni... etc..
Spero da neofita di essere stato chiaro.
Mi trovi concorde, la bellezza della matematica è nella sua libertà.
Scusa se non mi soffermo ma non ne ho il tempo al momento.
Se la tua domanda invece si riferisce al blog. E' nato come esperimento, per aprire uno spazio virtuale, dove far entrare idee di persone che solitamente non avrebbero grossi spazi. Se tu hai un racconto o vuoi scrivere un articolo o hai un' idea.
Scrivi alla mail e vedremo come fare e se possiamo aiutarti a esprimerla indipendentemente nel nostro spazio sul blog.
Almeno su 15 persone che hanno visto il post, qualcuno che si è incuriosito c'è. E sono contento che porti nel mess. una frase così bella. Grazie.
E cmq questo è il materiale meno importante, difatti è stato scelto come primo post.
Sicuramente dovrò aggiungerne un altro per indicare i paradossi di zenone e del cerchio, ma questo è poco importante il tempo c'è... e poi nulla esclude che qualcuno voglia avventurarsi da solo in rete, ansi se avete altre idee sui labirinti e ricordo che è affine ad un altro problema (del millenio) anche se non uguale, e cioè capire la strada più breve senza costi di computazione, scrivete non aspettiamo altro.
Puoi essere più specifico?
Di cosa si tratta!?
Di cosa si tratta!?




 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo