Dimostrazione teorema di pitagora alquanto ignorante

[kobeilprofeta]

Considera una scacchiera contenente $j^2$ caselle, ognuna quadrata e di lato $l$. Traccia le diagonali della scacchiera: ognuna delle due diagonali sarà la somma delle diagonali dei $j$ quadrati attraversati e chiama le diagonali dei singoli quadrati $d$. Ora prendi un insieme contente $n=j^2$ nomi di colori e crea una funzione biunivoca che associ ad ogni casella il nome di un colore. Questa funzione sarà definita $AA x in NN : 0 CVD

[kobeilprofeta]

"Zero87":[quote="kobeilprofeta"]Il fulcro era quello: che $d=sqrt(2)*l$ lo si ricava proprio da pitagora.

Chiedo scusa allora... però ho visto che non ero l'unico ad averla presa alla lettera. [/quote]

Tranquillo, l'ho messa giù male io

[nato_pigro1]

Per ma la più semplice in assoluto è la seguente:




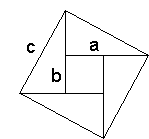
E una delle più strambe/carine/innovative e -in altro senso- didattiche è la 100 (l'ultima) di questo link:
http://www.cut-the-knot.org/pythagoras/index.shtml

[Zero87]

"kobeilprofeta":Il fulcro era quello: che $d=sqrt(2)*l$ lo si ricava proprio da pitagora.

Chiedo scusa allora... però ho visto che non ero l'unico ad averla presa alla lettera.

[kobeilprofeta]

"Zero87":...
Inizialmente ho pensato che $\sqrt(2)\cdot l$ lo si ricavava dal teorema di Pitagora ma poi mi sono ricordato che un quadrato non è altro che un caso particolare di rombo e, quindi, se so l'area ricavo la diagonale senza passare per il già citato Pitagora...!

Il fulcro era quello: che $d=sqrt(2)*l$ lo si ricava proprio da pitagora.


@gugo
Mi spiace vedere che non ti è piaciuto. L'ho trovata e sinceramente mi faceva sorridere per la convinzione.

[gugo82]

No, non si era capito. Affatto.

[kobeilprofeta]

Ok non si era capito. Era ironica.

[gugo82]

Sinceramente, non capisco cosa tu voglia dimostrare né cosa credi di aver dimostrato.

Una dimostrazione davvero bella, perché senza parole, è quella che si ottiene confrontando le seguenti due figure:
[asvg]xmin=0; xmax=17; ymin=-5; ymax=12;
noaxes();
fill="yellow"; path([[0,0],[3,0],[0,4],[0,0]]); path([[3,0],[7,0],[7,3],[3,0]]); path([[7,3],[7,7],[4,7],[7,3]]); path([[4,7],[0,7],[0,4],[4,7]]);
rect([10,0],[13,4]); line([10,4],[13,0]); rect([13,4],[17,7]); line([13,7],[17,4]);
fill="none"; path([[10,4],[10,7],[13,7]]); path([[13,0],[17,0],[17,4]]);
text([3.5,3.5],"c^2"); text([11.5,5.5],"a^2"); text([15,2],"b^2");[/asvg]

[Zero87]

Sinceramente non capisco la faccenda dei colori...
... ma comunque posso obiettare che l'hai dimostrato per dei triangoli rettangoli isosceli che sono un caso particolare dell'infinità dei vari tipi di triangoli rettangoli.

"kobeilprofeta":Sapendo che l'ipotenusa è la diagonale del quadrato di lato $ l $ e sapendo che la diagonale di un quadrato di lato $ l $ è pari a $ sqrt(2)*l $

Inizialmente ho pensato che $\sqrt(2)\cdot l$ lo si ricavava dal teorema di Pitagora ma poi mi sono ricordato che un quadrato non è altro che un caso particolare di rombo e, quindi, se so l'area ricavo la diagonale senza passare per il già citato Pitagora...!