Verfica densità congiunta e densità marginali
$ int_(-oo)^(oo)int_(-oo)^(oo) f(x,y) dx dy = int_(0)^(oo) int_(0)^(x) 2e^{-x-y} dy dx = int_(0)^(oo) 2*[-e^{-x-y}]_{0}^{x} dx = int_(0)^(oo) 2*e^{-x}(1-e^{-x}) dx= int_(0)^(oo) 2e^{-x}dx - int_(0)^(oo) 2e^{-2x} dx= [-2e^{-x}]_{0}^{oo} + 2*(1/2)[e^{-2x}]_{0}^{oo}$
Verificare che $f(x,y)=$\begin{cases}2e^{-y-x}&0<=y<=x \\0&altrimenti \end{cases} sia una densità congiunta di $(X,Y)$ e calcolare le densità $\rho_{X}, \rho_{Y}$.
Per controllare che sia una densità congiunta:
$ int_(-oo)^(oo)int_(-oo)^(oo) f(x,y) dx dy = 1$
$ int_(-oo)^(oo)int_(-oo)^(oo) f(x,y) dx dy = int_(0)^(oo) int_(0)^(x) 2e^{-x-y} dy dx = int_(0)^(oo) 2*[-e^{-x-y}]_{0}^{x} dx = int_(0)^(oo) 2*e^{-x}(1-e^{-x}) = int_(0)^(oo) 2e^{-x} - int_(0)^(oo) 2e^{-2x} = [-2e^{-x}]_{0}^{oo} + 2*(1/2)[e^{-2x}]_{0}^{oo}= 2 - 1 = 1$
La funzione in questione è una densità.
Per le densità marginali basta porre:
$\rho_{X} = int_(0)^(x) 2e^{-x-y} dy = 2e^{-x}-e^{-2x} = 2e^{-x}(1-e^{-x}) $
Ho un dubbio sulla riscrittura del sostegno per trovare la seguente. Quale delle due è corretta?
$\rho_{Y} = int_(y)^(oo) 2e^{-x-y} dx = 2e^{-2y}$
oppure
$\rho_{Y} = int_(0)^(oo) 2e^{-x-y} dx = 2e^{-y} $
Verificare che $f(x,y)=$\begin{cases}2e^{-y-x}&0<=y<=x \\0&altrimenti \end{cases} sia una densità congiunta di $(X,Y)$ e calcolare le densità $\rho_{X}, \rho_{Y}$.
Per controllare che sia una densità congiunta:
$ int_(-oo)^(oo)int_(-oo)^(oo) f(x,y) dx dy = 1$
$ int_(-oo)^(oo)int_(-oo)^(oo) f(x,y) dx dy = int_(0)^(oo) int_(0)^(x) 2e^{-x-y} dy dx = int_(0)^(oo) 2*[-e^{-x-y}]_{0}^{x} dx = int_(0)^(oo) 2*e^{-x}(1-e^{-x}) = int_(0)^(oo) 2e^{-x} - int_(0)^(oo) 2e^{-2x} = [-2e^{-x}]_{0}^{oo} + 2*(1/2)[e^{-2x}]_{0}^{oo}= 2 - 1 = 1$
La funzione in questione è una densità.
Per le densità marginali basta porre:
$\rho_{X} = int_(0)^(x) 2e^{-x-y} dy = 2e^{-x}-e^{-2x} = 2e^{-x}(1-e^{-x}) $
Ho un dubbio sulla riscrittura del sostegno per trovare la seguente. Quale delle due è corretta?
$\rho_{Y} = int_(y)^(oo) 2e^{-x-y} dx = 2e^{-2y}$
oppure
$\rho_{Y} = int_(0)^(oo) 2e^{-x-y} dx = 2e^{-y} $
Risposte
Suppongo che quella giusta sia questa: $ \rho_{Y} = int_(0)^(oo) 2e^{-x-y} dx = 2e^{-y} $.
Eppure non c'è una regola per cui l'ho scelta come corretta se non perché ho riscritto il dominio come:
$0<=x<=oo,0<=y<=x$. Mi è sfuggito qualcosa?
Eppure non c'è una regola per cui l'ho scelta come corretta se non perché ho riscritto il dominio come:
$0<=x<=oo,0<=y<=x$. Mi è sfuggito qualcosa?
supponi male. E' l'altra che evidentemente è una esponenziale negativa di media $1/2$
ma la domanda che mi pongo è: che problemi incontri nell'integrare rispetto ad $X$ il seguente dominio??
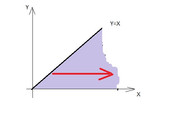
in definitiva la tua densità viene
$f_Y(y)=2e^(-2y)mathbb{1}_([0;+oo))(y)$
ovvero Y è distribuita marginalmente secondo una legge esponenziale negativa di media 0.5
Sì ti è sfuggito che per integrare rispetto ad $X$ devi riscrivere il dominio diversamente, ovvero semplice rispetto all'altro asse:
$D={(x,y) in RR^2: 0<=y
[ot]Questa però non è Statistica...qui ci sono lacune sulla matematica di base....[/ot]
ma la domanda che mi pongo è: che problemi incontri nell'integrare rispetto ad $X$ il seguente dominio??

in definitiva la tua densità viene
$f_Y(y)=2e^(-2y)mathbb{1}_([0;+oo))(y)$
ovvero Y è distribuita marginalmente secondo una legge esponenziale negativa di media 0.5
"ingetor":
Eppure non c'è una regola per cui l'ho scelta come corretta se non perché ho riscritto il dominio come:
$0<=x<=oo,0<=y<=x$. Mi è sfuggito qualcosa?
Sì ti è sfuggito che per integrare rispetto ad $X$ devi riscrivere il dominio diversamente, ovvero semplice rispetto all'altro asse:
$D={(x,y) in RR^2: 0<=y
[ot]Questa però non è Statistica...qui ci sono lacune sulla matematica di base....[/ot]
Mi pare di capire che la verifica della densità la potevo fare anche riscrivendo il dominio rispetto all'altro asse come hai scritto tu in fondo. E' esatto?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo