Variabili aleatorie indipendenti
Salve ragazzi e buona domenica. Non mi fermo mai 
"Siano $X$ e $Y$ due variabili aleatorie indipendenti con distribuzione uniforme in $[0,2]$. Sia inoltre $Z$ una terza variabile aleatoria definita come segue:
$ Z = { ( X if X>Y ),( 0 if otherwise ):} $
Calcolare:
$1)$ il valore atteso di $X + Y$;
$2)$ il valore atteso di $X*Y$;
$3)$ la probabilità che $Y>X$ [Suggerimento: si ragioni graficamente disegnando un diagramma cartesiano che abbia sull’asse $x$ la variabile $X$ e sull’asse $y$ la variabile $Y$ e quindi si disegni la retta $X$= $Y$ . Si identifichi quindi la regione cui si riferisce il quesito.];
$4)$ il valore medio di $Z$;
$5)$ la probabilità che $Z>1$.
[Risoluzione]
$1)$ Ho definito una nuova variabile aleatoria $S$ tale che $S = X + Y$.
Per linearità dell'operatore valore medio, ho calcolato che $E(S) = E(X) + E(Y) = 2$.
$2)$ Analogamente ho definito una nuova variabile aleatoria $P$ tale che $P = X * Y$.
$P$ dovrebbe essere nuovamente una uniforme in $[0,4]$ con valore medio $E(P) = 1/2*("lower"+"upper")$ dove $"lower" = 0$ e $"upper" = 4$ dunque anche in questo caso $E(P) = 2$.
$3)$ a questo punto ho fatto come suggerito, ho tracciato la retta $Y = X$ nonchè bisettrice del primo (e del terzo) quadrante, ottenendo due zone. Al di sotto della retta (andando verso destra in direzioni di $x$ crescenti, insomma) avremo $X > Y$. Al di sopra della retta, dunque verso valori crescenti di $Y$ avremo $XX) = 1/2$ ?
$4)$ $Z$ dovrebbe essere una distribuzione anch'essa uniforme, però devo prima analizzare bene in quale intervallo è definita. Posso in qualche modo riusare il grafico visto sopra per determinare i valori di $Z$ o devo fare qualcos'altro?? non mi viene nulla in mente
"Siano $X$ e $Y$ due variabili aleatorie indipendenti con distribuzione uniforme in $[0,2]$. Sia inoltre $Z$ una terza variabile aleatoria definita come segue:
$ Z = { ( X if X>Y ),( 0 if otherwise ):} $
Calcolare:
$1)$ il valore atteso di $X + Y$;
$2)$ il valore atteso di $X*Y$;
$3)$ la probabilità che $Y>X$ [Suggerimento: si ragioni graficamente disegnando un diagramma cartesiano che abbia sull’asse $x$ la variabile $X$ e sull’asse $y$ la variabile $Y$ e quindi si disegni la retta $X$= $Y$ . Si identifichi quindi la regione cui si riferisce il quesito.];
$4)$ il valore medio di $Z$;
$5)$ la probabilità che $Z>1$.
[Risoluzione]
$1)$ Ho definito una nuova variabile aleatoria $S$ tale che $S = X + Y$.
Per linearità dell'operatore valore medio, ho calcolato che $E(S) = E(X) + E(Y) = 2$.
$2)$ Analogamente ho definito una nuova variabile aleatoria $P$ tale che $P = X * Y$.
$P$ dovrebbe essere nuovamente una uniforme in $[0,4]$ con valore medio $E(P) = 1/2*("lower"+"upper")$ dove $"lower" = 0$ e $"upper" = 4$ dunque anche in questo caso $E(P) = 2$.
$3)$ a questo punto ho fatto come suggerito, ho tracciato la retta $Y = X$ nonchè bisettrice del primo (e del terzo) quadrante, ottenendo due zone. Al di sotto della retta (andando verso destra in direzioni di $x$ crescenti, insomma) avremo $X > Y$. Al di sopra della retta, dunque verso valori crescenti di $Y$ avremo $X
$4)$ $Z$ dovrebbe essere una distribuzione anch'essa uniforme, però devo prima analizzare bene in quale intervallo è definita. Posso in qualche modo riusare il grafico visto sopra per determinare i valori di $Z$ o devo fare qualcos'altro?? non mi viene nulla in mente
Risposte
"MrEngineer":
$2)$ Analogamente ho definito una nuova variabile aleatoria $P$ tale che $P = X * Y$.
$P$ dovrebbe essere nuovamente una uniforme in $[0,4]$ con valore medio $E(P) = 1/2*("lower"+"upper")$ dove $"lower" = 0$ e $"upper" = 4$ dunque anche in questo caso $E(P) = 2$.
...sta roba mi fa accapponare la pelle[nota]per calcolare la distribuzione di $W=XY$ (che non serve) dovresti calcolare l'area sotto il ramo di iperbole $Y
Per l'indipendenza si ha che $E[XY]=E[X]E[Y]$
Infatti se le variabili sono indipendenti a maggior ragione saranno anche non correlate
Z è uniforme? certo ma uniforme bidimensionale
$f_Z(z)=f_(XY)(x,y)=1/2 \mathbb{1}_([0;2]) (x)\mathbb{1}_([0;x])(y)$
per rendersene conto, senza fare alcun conto (la cacofonìa è voluta) basta fare l'area del triangolo in questione, moltiplicarlo per $1/2$ (che poi è proprio $f(x)$) e vedi che fa uno.
La sua media la calcoli con la definizione (per integrazione)
mentre la probabilità che $z>1$ è l'area del trapezio colorato moltiplicata per la densità, ovvero per $1/2$
(cliccami per ingrandirmi)
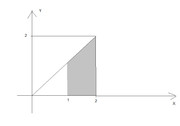
...lo so ho aiutato troppo...ma dai è la befana
(sono in giro e non ho fatto alcun conto....)
"tommik":
(sono in giro e non ho fatto alcun conto....)
Se avessi la tua capacità nel padroneggiare la materia,sarei già con un $30$ in tasca da un pezzo... ma il $30$ è solo un miraggio!!!
Mi scuso se volano baggianate ma non ho fatto granchè sulle variabili indipendenti.
Se $E(XY) = E(X)E(Y)$ allora $E(XY) = 1$. Per il resto, ora cerco di attenzionare per benino...
il punto $3)$ è corretto oppure ho fallito anche in quello?
"MrEngineer":
Se avessi la tua capacità nel padroneggiare la materia...
ho 55 anni e circa 30 di esperienza....anche se non faccio l'insegnante l'esperienza varrà pure qualche cosa no?
Il 3) è giusto anche se andrebbe meglio formalizzato.
Per calcolare la probabilità $X
"tommik":
ho 55 anni e circa 30 di esperienza....anche se non faccio l'insegnante l'esperienza varrà pure qualche cosa no?
Per carità, è ovvio che l'esperienza è tutto! Il mio voleva essere un complimento
Tutor AI
Ciao! Sono il tuo Tutor AI, il compagno ideale per uno studio interattivo. Utilizzo il metodo maieutico per affinare il tuo ragionamento e la comprensione. Insieme possiamo:
- Risolvere un problema di matematica
- Riassumere un testo
- Tradurre una frase
- E molto altro ancora...
Il Tutor AI di Skuola.net usa un modello AI di Chat GPT.
Per termini, condizioni e privacy, visita la relativa pagina.
Per termini, condizioni e privacy, visita la relativa pagina.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo