Trasformazione v.a.
Siano X e Y v.a. indipendenti e i.d. con legge Exp(1).
Trovare la distibuzione di Z=Y-X.
Essendo esponenziali, X>0 e Y>0, quindi direi che Z(-$oo$,+$oo$).
Ore per trovare la Fz mi cacolo P(Y$<=$z+X)
Essendo indipendenti fxy(x,y)=fx(x)fy(y).
Ora devo quindi calcolarmi l'integrale doppio per trovare la fz(z).
La soluzione del mio libro mi dstingue i due casi z$>=$0 e z$<$0. La prima cosa che non capisco è perchè, se diide nei vari casi, non lo fa anche per z=0, visto che a parer mio varierebbero gli estremi di integrazione tra z=0 e z$>=$0.
L'altro dubbio è quindi sugli estremi di integrazione.
Per z<0, io farei $int_0^(+oo)dxint_0^(z+x)dy$ mentre la soluzione scrive $int_(-z)^(+oo)dxint_0^(z+x)dy$
perchè da -z e non 0?
se z per esempio valesse -2, perchè dovrei integrare da -(-2) e on da 0?
Per z$>=$0 io metterei $int_z^(+oo)dxint_0^(z+x)dy$, mentre la soluzione è $int_(0)^(+oo)dxint_0^(z+x)dy$
in questo caso, se z>0, perchè parte da 0 e non da z?
Il dominio non dovrebbe essere così?
Trovare la distibuzione di Z=Y-X.
Essendo esponenziali, X>0 e Y>0, quindi direi che Z(-$oo$,+$oo$).
Ore per trovare la Fz mi cacolo P(Y$<=$z+X)
Essendo indipendenti fxy(x,y)=fx(x)fy(y).
Ora devo quindi calcolarmi l'integrale doppio per trovare la fz(z).
La soluzione del mio libro mi dstingue i due casi z$>=$0 e z$<$0. La prima cosa che non capisco è perchè, se diide nei vari casi, non lo fa anche per z=0, visto che a parer mio varierebbero gli estremi di integrazione tra z=0 e z$>=$0.
L'altro dubbio è quindi sugli estremi di integrazione.
Per z<0, io farei $int_0^(+oo)dxint_0^(z+x)dy$ mentre la soluzione scrive $int_(-z)^(+oo)dxint_0^(z+x)dy$
perchè da -z e non 0?
se z per esempio valesse -2, perchè dovrei integrare da -(-2) e on da 0?
Per z$>=$0 io metterei $int_z^(+oo)dxint_0^(z+x)dy$, mentre la soluzione è $int_(0)^(+oo)dxint_0^(z+x)dy$
in questo caso, se z>0, perchè parte da 0 e non da z?
Il dominio non dovrebbe essere così?
Risposte
Il libro ha ragione.
Ecco il grafico del dominio; a sinistra il caso in cui $z<0$, a destra il caso in cui $z>0$
(cliccami per ingrandirmi)
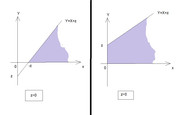
Il caso $z=0$ non ci interessa perché la distribuzione è continua e dunque $P[Z=k]=0$ $AAk$
guardando il dominio vedi subito i corretti estremi di integrazione per trovare la $F_Z(z)$
$F_Z(z)=int_(-z)^(+oo)f(x)dxint_0^(x+z)f(y)dy$
$F_Z(z)=int_(0)^(+oo)f(x)dxint_0^(x+z)f(y)dy$
Ecco il grafico del dominio; a sinistra il caso in cui $z<0$, a destra il caso in cui $z>0$
(cliccami per ingrandirmi)
Il caso $z=0$ non ci interessa perché la distribuzione è continua e dunque $P[Z=k]=0$ $AAk$
guardando il dominio vedi subito i corretti estremi di integrazione per trovare la $F_Z(z)$
$F_Z(z)=int_(-z)^(+oo)f(x)dxint_0^(x+z)f(y)dy$
$F_Z(z)=int_(0)^(+oo)f(x)dxint_0^(x+z)f(y)dy$
Grazie, mi ero bloccata per una banalità. Continuo a non capire invece perchè non interessi z=0... Anche perchè il libro non è che la omette ma me la calcola con z$>=$0
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo