Prodotti di convoluzione e somma di variabili aleatorie
Posto qui e non in Statistica e Probabilità in quanto è un topic un po' più matematico che non altro.
Dunque, mi trovo a dover ricavare la funzione di densità della somma di tre variabili casuali uniformi (0,1) (o rettangolari che dir si voglia, o Beta(1,1))
dette variabili sono indipendenti, per cui al punto prima dell'esercizio, dove mi chiedeva la somma di due di esse, ho applicato il prodotto di convoluzione
e ho ricavato la mia brava distribuzione triangolare.
la mia domanda è questa: devo ripartire da capo e fare una trasformazione di variabili classica, oppure posso applicare ancora una volta la convoluzione fra
la somma delle prime due (che ho, appunto, già ricavato) e la terza uniforme?
ovvero, posso dire che:
$S=X_1+X_2
$W=X_1+X_2+X_3
$f_W=f_S ** f_(X_3)
?
Dunque, mi trovo a dover ricavare la funzione di densità della somma di tre variabili casuali uniformi (0,1) (o rettangolari che dir si voglia, o Beta(1,1))
dette variabili sono indipendenti, per cui al punto prima dell'esercizio, dove mi chiedeva la somma di due di esse, ho applicato il prodotto di convoluzione
e ho ricavato la mia brava distribuzione triangolare.
la mia domanda è questa: devo ripartire da capo e fare una trasformazione di variabili classica, oppure posso applicare ancora una volta la convoluzione fra
la somma delle prime due (che ho, appunto, già ricavato) e la terza uniforme?
ovvero, posso dire che:
$S=X_1+X_2
$W=X_1+X_2+X_3
$f_W=f_S ** f_(X_3)
?
Risposte
Si: $f_(X_1+X_2+X_3)=f_(X_1) ** f_(X_2) ** f_(X_3)=f_(X_1) **( f_(X_2) ** f_(X_3))=(f_(X_1) ** f_(X_2)) ** f_(X_3)=ldots$
dunque è associativa..grazie mille
ora devo solo cavarmene fuori con i domini di integrazione...sono un danno
ora devo solo cavarmene fuori con i domini di integrazione...sono un danno
"Chicco_Stat_":
ora devo solo cavarmene fuori con i domini di integrazione...sono un danno
Intendi in questo caso?
si
per il caso di due variabili me la sono cavata, posto
${(S=X_1+X_2),(T=X_2):}$
quindi
${(X_1=S-T),(X_2=T):}$
e siccome $0
$f_S(s)={(int_0^s dt = s, 0
però ora non riesco a cavarmela con le tre variabili (lo so, è una boiata, ma forse sbaglio ragionamento..)
${(W=S+X_3),(U=X_3):}$
quindi
${(S=W-U),(X_3=U):}$
e deve valere ${(0
mi viene da dire: spezzo in tre parti
per la prima considero $0
$f_W(w)=int_0^w f_s(w-u)f_(X_3)(u)du = int_0^w (w-u)du = w^2/2$
ma, posto che sia giusto, mi blocco per la determinazione degli estremi per $1<=w<2$ e $2<=w<3$
per il caso di due variabili me la sono cavata, posto
${(S=X_1+X_2),(T=X_2):}$
quindi
${(X_1=S-T),(X_2=T):}$
e siccome $0
$f_S(s)={(int_0^s dt = s, 0
però ora non riesco a cavarmela con le tre variabili (lo so, è una boiata, ma forse sbaglio ragionamento..)
${(W=S+X_3),(U=X_3):}$
quindi
${(S=W-U),(X_3=U):}$
e deve valere ${(0
mi viene da dire: spezzo in tre parti
per la prima considero $0
$f_W(w)=int_0^w f_s(w-u)f_(X_3)(u)du = int_0^w (w-u)du = w^2/2$
ma, posto che sia giusto, mi blocco per la determinazione degli estremi per $1<=w<2$ e $2<=w<3$
"elgiovo":
Si: $f_(X_1+X_2+X_3)=f_(X_1) ** f_(X_2) ** f_(X_3)=f_(X_1) **( f_(X_2) ** f_(X_3))=(f_(X_1) ** f_(X_2)) ** f_(X_3)=ldots$
toglietemi un dubbio:
per rispondere alla prima domanda posta da chicco, secondo me non e' necessario sapere che la convoluzione e' associativa.
cioe' io gli avrei risposto: si', in quanto stai semplicemente riapplicando una regola che hai applicato per la somma delle prime 2. sbaglio?
eh ma la densità di una somma di variabili aleatorie coincide con la convoluzione solo se dette variabili sono indipendenti, quindi al limite questo è un caso particolare..non penso basti dire "ho già applicato alle prime due", non sapendo che la convoluzione fosse un operatore lineare non avrei potuto concludere così tanto per, credo 
Quando si ha a che fare con funzioni rettangolari o triangolari a mio avviso conviene procedere per via grafica.
In questo caso devi convolvere una funzione triangolare con una rettangolare. Fissando la prima, ribaltando la seconda e facendola scorrere si vede che devi distinguere i cinque casi $w<0$, $03$ (che poi si riducono a 3 vista la simmetria delle d.d.p.).
Un suggerimento, più che altro per verificare l'esattezza delle tue convoluzioni: se le d.d.p. da convolvere hanno supporti $S_1$ e $S_2$ di misura $|S_1|$ e $|S_2|$ in genere la misura del supporto della convoluzione è $|S_1|+|S_2|$ (scusa il gergo un pò matematico, in genere si parla di banda e occupazione spettrale, ma non è proprio questo il contesto). Nel tuo caso, infatti, convolvendo un triangolo con supporto di misura $2$ e un rettangolo con supporto di misura $1$, ottieni una funzione con supporto di misura $3$.
In questo caso devi convolvere una funzione triangolare con una rettangolare. Fissando la prima, ribaltando la seconda e facendola scorrere si vede che devi distinguere i cinque casi $w<0$, $0
Un suggerimento, più che altro per verificare l'esattezza delle tue convoluzioni: se le d.d.p. da convolvere hanno supporti $S_1$ e $S_2$ di misura $|S_1|$ e $|S_2|$ in genere la misura del supporto della convoluzione è $|S_1|+|S_2|$ (scusa il gergo un pò matematico, in genere si parla di banda e occupazione spettrale, ma non è proprio questo il contesto). Nel tuo caso, infatti, convolvendo un triangolo con supporto di misura $2$ e un rettangolo con supporto di misura $1$, ottieni una funzione con supporto di misura $3$.
avevo escluso $w<0$ e $w>3$ in quanto per quei valori la funzione risultante è zero
mi spiegheresti meglio che intendi con "fissando la prima, ribaltando la seconda e facendola scorrerre" ?
mi spiegheresti meglio che intendi con "fissando la prima, ribaltando la seconda e facendola scorrerre" ?
"Chicco_Stat_":
mi spiegheresti meglio che intendi con "fissando la prima, ribaltando la seconda e facendola scorrerre" ?
E' l'interpretazione grafica della convoluzione. Si fissa uno dei due segnali, si ribalta il secondo, lo si fa scorrere sull'asse delle ascisse da sinistra a destra e di volta in volta si calcola l'area del loro prodotto. Questa immagine di Wikipedia aiuta:
Anche meglio questa gif di MathWorld:
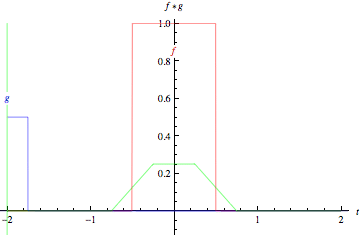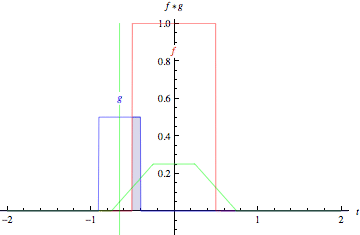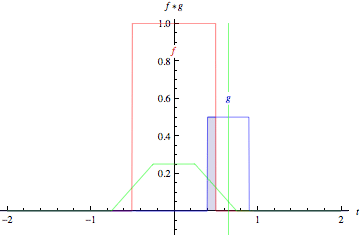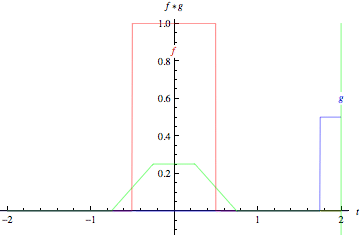
Qui addirittura puoi divertirti creando segnali a tuo piacimento.
molto carina..ma sono punto e a capo temo 
non ho mai studiato teoria dei segnali o cose del genere, quindi è la prima volta che vedo queste rappresentazioni...continuo a non capire come possano essermi d'aiuto per individuare i corretti estremi di integrazione..grazie per la pazienza
non ho mai studiato teoria dei segnali o cose del genere, quindi è la prima volta che vedo queste rappresentazioni...continuo a non capire come possano essermi d'aiuto per individuare i corretti estremi di integrazione..grazie per la pazienza
Il fatto che mi sia erroneamente uscito un "segnali" al posto di "funzioni" non implica che tu non possa capire il meccanismo grafico della convoluzione, e di conseguenza saperti trovare gli estremi di integrazione: dopotutto è lo stesso metodo che cercavi di applicare qualche post più su. In sostanza, devi distinguere i casi in cui il rettangolo e il triangolo non sono sovrapposti, lo sono parzialmente o lo sono totalmente; è così che ho determinato la casistica prima. Fidati, è il modo migliore (se non si può usare un computer) per il calcolo di questi integrali.
direi che questo potrebbe essere tranquillamente un post da statistica e probabilità!
il calcolo delle probabilità non è urne e testa e croce! in un corso di calcolo delle probbilità 2 di statistica si fa molto approfonditamente la convoluzione di v.a.
insomma questo è calcolo delle prob (MAT/06)!!!!!
!
il calcolo delle probabilità non è urne e testa e croce! in un corso di calcolo delle probbilità 2 di statistica si fa molto approfonditamente la convoluzione di v.a.
insomma questo è calcolo delle prob (MAT/06)!!!!!
!
Ho provato a rosolvere l'esercizio (3 uniformi 0,1) ma ho paura di aver sbagliato.
Mi potete dare la pdf?
Mi potete dare la pdf?
La somma di tre uniformi in (0,1) ha densità:
$x^2/2$ per $x in (0,1)$;
$3/4-(x-3/2)^2$ per $x in (1,2)$;
$(3-x)^2/2$ per $x in (2,3)$;
$0$ altrove.
$x^2/2$ per $x in (0,1)$;
$3/4-(x-3/2)^2$ per $x in (1,2)$;
$(3-x)^2/2$ per $x in (2,3)$;
$0$ altrove.
Come al solito sei un grande!
Comunque,
Definendo $X_1+X_2= Y$ cerco $S=Y+X_3$
Uso la regola
$int_ (-oo)^(oo) f_y(s-x_3) f_(x_3)(x_3)dx_3$
Ed usando la pdf della triangolare ottengo (sbagliando)
$int_ (0)^(s) (s-x_3) $ per $0
$int_ (s-1)^(1) 2-(s-x_3) $ per $1
$int_ (s-2)^(1) 2-(s-x_3) $ per $2
Il primo ed il terzo pezzo mi danno i tuio risultati quidi forse vanno bene, ma il secondo no. Dove sta l’errore? Che regola si usa per definire gli spazi di integrazione?
Comunque,
Definendo $X_1+X_2= Y$ cerco $S=Y+X_3$
Uso la regola
$int_ (-oo)^(oo) f_y(s-x_3) f_(x_3)(x_3)dx_3$
Ed usando la pdf della triangolare ottengo (sbagliando)
$int_ (0)^(s) (s-x_3) $ per $0
$int_ (s-1)^(1) 2-(s-x_3) $ per $1
$int_ (s-2)^(1) 2-(s-x_3) $ per $2
Il primo ed il terzo pezzo mi danno i tuio risultati quidi forse vanno bene, ma il secondo no. Dove sta l’errore? Che regola si usa per definire gli spazi di integrazione?
Se i risultati sono gli stessi i calcoli dovrebbero essere giusti anche se nel primo e nel terzo io ho delle cose leggermente differenti.
per il secondo $int_(s-1)^1 y dy\ +\ int_1^s (2-y) dy$ questo perchè la densità y cambia a seconda che y è in (0,1) o (1,2).
Gli estremi di integrazioni sono determinati dai valori per i quali le densità $f_y$ e $f_(x_3))$ non si annullano (o al di fuori di quelli l'integrando è 0).
per il secondo $int_(s-1)^1 y dy\ +\ int_1^s (2-y) dy$ questo perchè la densità y cambia a seconda che y è in (0,1) o (1,2).
Gli estremi di integrazioni sono determinati dai valori per i quali le densità $f_y$ e $f_(x_3))$ non si annullano (o al di fuori di quelli l'integrando è 0).
mi sbagliavo i conti mi tornano solo nel primo mio integrale.
Tuttavia se hai la pazienza di spiegarmi vorrei ripartire dalla somma di 2 uniformi $X_1+X_2$, i problemi ho paura partano da li.
In sostanza cerco di applicare la formula generale scritta sopra,siccome le densità sono entrambe 1 metto dx e faccio che ragionare solo sugli estremi d'integrazione. Dopodiché
$P(z-x_2<0)=0$ da cui $P(x_2>z)=0$ e $z$ diventa l'estremo superiore dell'integrale quando siamo su (0,1). Poi a dire il vero come far saltar fuori gli estremi dell'integrale valido per lo spazio (1,2), sinceramente mi sfugge.
Tuttavia se hai la pazienza di spiegarmi vorrei ripartire dalla somma di 2 uniformi $X_1+X_2$, i problemi ho paura partano da li.
In sostanza cerco di applicare la formula generale scritta sopra,siccome le densità sono entrambe 1 metto dx e faccio che ragionare solo sugli estremi d'integrazione. Dopodiché
$P(z-x_2<0)=0$ da cui $P(x_2>z)=0$ e $z$ diventa l'estremo superiore dell'integrale quando siamo su (0,1). Poi a dire il vero come far saltar fuori gli estremi dell'integrale valido per lo spazio (1,2), sinceramente mi sfugge.
"markowitz":
Tuttavia se hai la pazienza di spiegarmi vorrei ripartire dalla somma di 2 uniformi $X_1+X_2$, i problemi ho paura partano da li.
Va bene.
La formula di convoluzione è: $f_(X_1+X_2)(y)=int_(RR) f_(X_1)(y-x)f_(X_2)(x) dx$
Ora $Y=X_1+X_2$ appartiene q.c. a (0,2) quindi $f_Y(y)=0$ fuori da (0,2).
Quindi lavoriamo su $y in (0,2)$. Dalla formula di convoluzione l'integranda è: $f_(X_1)(y-x)f_(X_2)(x)$ dove entrambe le funzioni sono della uniforme in (0,1) quindi valgono 0 se il loro argomento è fuori (0,1); 1 se è dentro.
Quindi l'integranda è non nulla quando: $y-x in (0,1)$ (che viene da $f_(X_1)$) e $x in (0,1)$ dalla seconda. Ora stiamo integrando in x quindi devi trovare delle condizioni espicite in x. La seconda è gia pronta; la prima la puoi riscrivere come $y-1
Hai quindi le due condizioni:
i) $y-1
Di questi ne devi fare l'intersezione; però il loro comportamento dipende dal valore che ha assunto y (ed è qua che salta fuori la divisione dei due casi $y in (0,1)$ e $y in (1,2)$).
Intersecando i) e ii) nel primo caso ottieni $0
Quindi la densità è nulla fuori da (0,2) ed i lati obliqui del triangolo (è rettangolo quindi sono i due cateti) di vertici (0,0); (1,1); (2,0).


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo