Problema gioco delle buste
Buongiorno a tutti, scrivo per esporre un dubbio.
Tempo fa lessi un articolo che si ispirava ad un gioco televisivo americano. Il concorrente sceglie una fra tre buste (A, B oppure C); una contiene un premio, le altre nulla. Fatta la scelta, il presentatore apre una delle due rimaste mostrando che non contiene nulla e chiede al concorrente se intende tenere la busta scelta o cambiarla con quella rimasta. Se il concorrente cambia la busta, la probabilità di vincere è maggiore, uguale o minore che non quella nel caso in cui invece si tenga la propria? L'articolo risolve la faccenda così: supponiamo che la busta col premio sia la C; allora tre casi:
1. il concorrente sceglie la A, ovviamente il presentatore gli fa vedere che nella B non c'è nulla, quindi se tiene la busta perde, se la cambia (con la C che è rimasta) vince;
2. il concorrente sceglie la B, ovviamente il presentatore gli fa vedere che nella A non c'è nulla, quindi se tiene la busta perde, se la cambia (con la C che è rimasta) vince;
3. il concorrente sceglie la C ; il presentatore apre indifferentemente la A o la B, in ogni caso se il concorrente tiene la busta vince, se la cambia perde.
Conclusione: se cambia la busta, in due casi vince ed in uno perde quindi la probabilità (subordinata) di vincere cambiando busta è $2/3$.
Mi pare ci sia una falla nel ragionamento. Credo che il caso 3. sia in realtà da scomporre in due casi elementari:
3.1 il concorrente sceglie la C ; il presentatore apre la A , se il concorrente tiene la busta vince, se la cambia perde;
3.2 il concorrente sceglie la C ; il presentatore apre la B , se il concorrente tiene la busta vince, se la cambia perde.
Così gli esiti possibili diventano $8$, in $4$ dei quali il concorrente vince cambiando la busta e pertanto la probabilità di vincita rimane la stessa indipendentemente dalla scelta fatta.
Chi ha ragione?
Tempo fa lessi un articolo che si ispirava ad un gioco televisivo americano. Il concorrente sceglie una fra tre buste (A, B oppure C); una contiene un premio, le altre nulla. Fatta la scelta, il presentatore apre una delle due rimaste mostrando che non contiene nulla e chiede al concorrente se intende tenere la busta scelta o cambiarla con quella rimasta. Se il concorrente cambia la busta, la probabilità di vincere è maggiore, uguale o minore che non quella nel caso in cui invece si tenga la propria? L'articolo risolve la faccenda così: supponiamo che la busta col premio sia la C; allora tre casi:
1. il concorrente sceglie la A, ovviamente il presentatore gli fa vedere che nella B non c'è nulla, quindi se tiene la busta perde, se la cambia (con la C che è rimasta) vince;
2. il concorrente sceglie la B, ovviamente il presentatore gli fa vedere che nella A non c'è nulla, quindi se tiene la busta perde, se la cambia (con la C che è rimasta) vince;
3. il concorrente sceglie la C ; il presentatore apre indifferentemente la A o la B, in ogni caso se il concorrente tiene la busta vince, se la cambia perde.
Conclusione: se cambia la busta, in due casi vince ed in uno perde quindi la probabilità (subordinata) di vincere cambiando busta è $2/3$.
Mi pare ci sia una falla nel ragionamento. Credo che il caso 3. sia in realtà da scomporre in due casi elementari:
3.1 il concorrente sceglie la C ; il presentatore apre la A , se il concorrente tiene la busta vince, se la cambia perde;
3.2 il concorrente sceglie la C ; il presentatore apre la B , se il concorrente tiene la busta vince, se la cambia perde.
Così gli esiti possibili diventano $8$, in $4$ dei quali il concorrente vince cambiando la busta e pertanto la probabilità di vincita rimane la stessa indipendentemente dalla scelta fatta.
Chi ha ragione?
Risposte
intanto leggi qui. E' lo stesso esercizio più generalizzato proposto da un utente.
poi, just in case, cercherò di dipanare meglio il tuo dubbio. La scelta è indifferente se il presentatore non conosce il contenuto delle buste altrimenti no.
poi, just in case, cercherò di dipanare meglio il tuo dubbio. La scelta è indifferente se il presentatore non conosce il contenuto delle buste altrimenti no.
A mio avviso la spiegazione migliore è con il teorema di Bayes[nota]vedi link che ho messo nel precedente post[/nota]ma vediamo di spiegarlo in modo differente (ho voglia di farmi del male  )
)
Non proprio...
Sì in effetti ci sono 8 eventi elementari: 4 dove si cambia e 4 dove si tiene; in entrambi i casi ci sono 2 casi in cui si vince e 2 casi in cui si perde....ma non tutti gli 8 eventi sono equiprobabili, e ciò a causa dell'asimmetria di informazioni fra Presentatore (che sa dove c'è il premio) e Concorrente (che invece non lo sa)
Ecco una tabellina dove ho supposto che il concorrente scelga se Cambiare o Tenere lanciando una moneta[nota]stessa ipotesi anche per il Presentatore nel caso debba aprire A oppure B se il Concorrente sceglie la busta giusta, ovvero C[/nota], supponendo che il premio sia in C:
(cliccami per ingrandirmi)
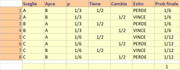
Come vedi, l'accoppiata Cambia-Vince ha probabilità $2/6$ mentre l'accoppiata Tiene-Vince ha probabilità $1/6$, ovvero la metà.
Il che equivale a dire che la probabilità di vincere dato che Cambia è $2/3$ menntre la probabilità di Vincere dato che Tiene è $1/3$ cioè lo stesso risultato ottenuto con Bayes.
Ora dovrebbe essere chiaro.
Nell'esempio del link precedente postato da @Gughigt l'esercizio era più articolato ma la sostanza è la stessa.
"Palliit":
Così gli esiti possibili diventano $8$, in $4$ dei quali il concorrente vince cambiando la busta e pertanto la probabilità di vincita rimane la stessa indipendentemente dalla scelta fatta.
Non proprio...
Sì in effetti ci sono 8 eventi elementari: 4 dove si cambia e 4 dove si tiene; in entrambi i casi ci sono 2 casi in cui si vince e 2 casi in cui si perde....ma non tutti gli 8 eventi sono equiprobabili, e ciò a causa dell'asimmetria di informazioni fra Presentatore (che sa dove c'è il premio) e Concorrente (che invece non lo sa)
Ecco una tabellina dove ho supposto che il concorrente scelga se Cambiare o Tenere lanciando una moneta[nota]stessa ipotesi anche per il Presentatore nel caso debba aprire A oppure B se il Concorrente sceglie la busta giusta, ovvero C[/nota], supponendo che il premio sia in C:
(cliccami per ingrandirmi)

Come vedi, l'accoppiata Cambia-Vince ha probabilità $2/6$ mentre l'accoppiata Tiene-Vince ha probabilità $1/6$, ovvero la metà.
Il che equivale a dire che la probabilità di vincere dato che Cambia è $2/3$ menntre la probabilità di Vincere dato che Tiene è $1/3$ cioè lo stesso risultato ottenuto con Bayes.
Ora dovrebbe essere chiaro.
Nell'esempio del link precedente postato da @Gughigt l'esercizio era più articolato ma la sostanza è la stessa.
 grazie mille!
grazie mille!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo