Problema di Statistica: Urna e Palline!
Ciao a tutti, volevo chiedere un aiuto a proposito di questo esercizietto di statistica. Sareste gentili rispondendo alla domanda e chiarendo ogni passaggio. Grazie in anticipo.
Es:
Si dispone di un urna nella quale vengono agitate 12 palline. Ognuna di esse è contrassegnata da un numero e nel dettaglio:
1 pallina con il numero 1
1 pallina con il numero 2
4 palline con il numero 3
1 pallina con il numero 4
1 pallina con il numero 5
2 palline con il numero 6
1 pallina con il numero 12
1 pallina con il numero 13
Dopo 4 estrazioni (senza reimmissione), sommando i numeri riportati sulle palline estratte, si è raggiunto un totale di 22.
Calcolare la probabilità alla 5 estrazione di pescare una pallina con il numero 3 tra le 8 rimaste.
Es:
Si dispone di un urna nella quale vengono agitate 12 palline. Ognuna di esse è contrassegnata da un numero e nel dettaglio:
1 pallina con il numero 1
1 pallina con il numero 2
4 palline con il numero 3
1 pallina con il numero 4
1 pallina con il numero 5
2 palline con il numero 6
1 pallina con il numero 12
1 pallina con il numero 13
Dopo 4 estrazioni (senza reimmissione), sommando i numeri riportati sulle palline estratte, si è raggiunto un totale di 22.
Calcolare la probabilità alla 5 estrazione di pescare una pallina con il numero 3 tra le 8 rimaste.
Risposte
Il numero 22, con quattro valori, si può comporre:
2+3+4+13;
3+3+3+13;
mi pare che non ci sono altre possibilità, pertanto nella prima configurazione la probabilità è 3/8, mentre nella seconda è 1/8
2+3+4+13;
3+3+3+13;
mi pare che non ci sono altre possibilità, pertanto nella prima configurazione la probabilità è 3/8, mentre nella seconda è 1/8
Qual è il procedimento generale nel caso ci fossero n configurazioni da considerare invece di 2? La probabilità è una, non credo si debbano considerare tutti i casi (nel caso fossero molto alti diventerebbe impossibile...). Fatemi sapere. Grazie
"IvanTerr":
Il numero 22, con quattro valori, si può comporre:
2+3+4+13;
3+3+3+13;
mi pare che non ci sono altre possibilità, pertanto nella prima configurazione la probabilità è 3/8, mentre nella seconda è 1/8
Ve ne sono altre:
13+6+2+1
13+5+3+1
Ci sono anche le possibilità con il numero 12 come:
12+6+3+1
12+5+4+1
12+5+3+2
12+4+3+3.
Ragazzi nessuno saprebbe aiutarmi un po' di più?
Potresti cominciare con il dettagliare tutti i modi per raggiungere 22, come hanno cominciato a fare IvanTerr e Mamo.
I possibili modi di raggruppare 4 palline prese dall'urna è dato da:
(12!) / 4!(12-4)!4!2!
dove il coefficiente binomiale dà tutti i modi di raggruppare 4 palline tra le 12 e il 4!2! è dovuto al fatto che ci sono 4 palline col numero 3 e 2 col numero 6.
Può essere giusto quello che ho scritto?
Comunque una volta trovato il numero totale di modi di estrarne 4, si devono isolare quelli col punteggio richiesto. Ma io mi chiedo: si deve per forza stare a contarli tutti (cosa che mi era già venuta in mente e in questo caso non è poi nanche molto complicato) o c'è un modo più veloce? Magari potrebbero esserci migliaia diversi casi possibili in un altra situazione.
E infine la domanda finale: sapendo che si è ottenuto 22 si chiede la probabilità che alla 5 estrazione si ottenga 25.
Non so potrebbe essere utile sapere che la media dei punteggi delle 4 estrazioni è 22/4 e con la nuova estrazione si sposta a 5?
Comunque mi piacerebbe avere risposta più a questo caso che all'esercizio:
Sia un urna con (a1,a2...an) palline dove (f1,f2...fn) è la frequenza di ogni pallina e (k1,k2...kn) il valore ad esse associato.
Si sa poi che dopo m estrazioni la sommatoria dei punteggi delle m palline è s. Determinare la probabilità che alla
(m+1)esima estrazione la sommatoria dei punteggi delle m+1 palline sia s+ki, dove ki è uno dei valori (k1,k2...kn).
Grazie
(12!) / 4!(12-4)!4!2!
dove il coefficiente binomiale dà tutti i modi di raggruppare 4 palline tra le 12 e il 4!2! è dovuto al fatto che ci sono 4 palline col numero 3 e 2 col numero 6.
Può essere giusto quello che ho scritto?
Comunque una volta trovato il numero totale di modi di estrarne 4, si devono isolare quelli col punteggio richiesto. Ma io mi chiedo: si deve per forza stare a contarli tutti (cosa che mi era già venuta in mente e in questo caso non è poi nanche molto complicato) o c'è un modo più veloce? Magari potrebbero esserci migliaia diversi casi possibili in un altra situazione.
E infine la domanda finale: sapendo che si è ottenuto 22 si chiede la probabilità che alla 5 estrazione si ottenga 25.
Non so potrebbe essere utile sapere che la media dei punteggi delle 4 estrazioni è 22/4 e con la nuova estrazione si sposta a 5?
Comunque mi piacerebbe avere risposta più a questo caso che all'esercizio:
Sia un urna con (a1,a2...an) palline dove (f1,f2...fn) è la frequenza di ogni pallina e (k1,k2...kn) il valore ad esse associato.
Si sa poi che dopo m estrazioni la sommatoria dei punteggi delle m palline è s. Determinare la probabilità che alla
(m+1)esima estrazione la sommatoria dei punteggi delle m+1 palline sia s+ki, dove ki è uno dei valori (k1,k2...kn).
Grazie
Posso dire una cosa: questo forum è deludente. Molte persone che leggono e nessuno che si degni anche di dire un banale e modesto "non lo so".
"Eric":
Posso dire una cosa: questo forum è deludente. Molte persone che leggono e nessuno che si degni anche di dire un banale e modesto "non lo so".
Non lo so.
Ciao.
Ciao Eric,
a prima vista mi verrebbe da dire che, salvo situazioni particolari, non vi sono metodi veloci che evitano di enumerare tutte le possibilità che danno per somma 22 con le quattro estrazioni. Credo che devi contarle tutte (condivido con te: in questo caso è facile, in altri potrebbe essere lunghissimo!), calcolare la probabilità che esca un 3 alla quinta in corrispondenza di ognuna di dette possibilità e poi basterà fare la media aritmetica tra le suddette probabilità per avere l'unica risposta richiesta dal problema.
a prima vista mi verrebbe da dire che, salvo situazioni particolari, non vi sono metodi veloci che evitano di enumerare tutte le possibilità che danno per somma 22 con le quattro estrazioni. Credo che devi contarle tutte (condivido con te: in questo caso è facile, in altri potrebbe essere lunghissimo!), calcolare la probabilità che esca un 3 alla quinta in corrispondenza di ognuna di dette possibilità e poi basterà fare la media aritmetica tra le suddette probabilità per avere l'unica risposta richiesta dal problema.
luluemicia,
condivido. In effetti, era lo stesso suggerimento che gli avevo dato io.
Sembra un post inutile, questo?
No! Mi vale per il conteggio dei post.
[size=75]Perdonate la meschinità, ma oggi sono cattivo. Come gli altri giorni.[/size]
condivido. In effetti, era lo stesso suggerimento che gli avevo dato io.
Sembra un post inutile, questo?
No! Mi vale per il conteggio dei post.
[size=75]Perdonate la meschinità, ma oggi sono cattivo. Come gli altri giorni.[/size]
Una nota terminologica a margine: si tratta di un problema (banale e seccante, forse per questo nessuno si è voluto mettere a far conti) di Calcolo delle Probabilità e non di Statistica come riportato nel titolo.
[size=75]Vale la stesa considerazione fatta da FP.[/size]
[size=75]Vale la stesa considerazione fatta da FP.[/size]
Grazie a tutti per l'aiuto, comunque ho trovato un modo per approssimare molto bene la soluzione di questo problema e altri simili senza stare a contare i casi possibili. che alcuni trovino banali questioni di questo tipo posso capirlo (anche se pensandoci bene la mia questione non era cosi banale, infatti il modo che ho trovato è molto interessante) ma non capisco perchè scrivere, o meglio scrivere solo per avere un post in più... ma vabbè avevo già capito la sostanza di molti forumisti...
ciao ciao
ciao ciao
ah comunque non è colpa mia se l'esame che ha sollevato il problema si chiama statistica e non probabilità...
che bello un post in più! ma si vincono dei premi?
che bello un post in più! ma si vincono dei premi?
Un po vecchiotto come topic, pero' ....
direi che parallelamente a trovare le soluzioni possibili, è necessario sapere anche quante volte possa capitare.
Ne ho trovate 33 anche se raggruppate in 8 possibili soluzioni.
Ognuna delle 33 puo' avere 8 soluzioni (una per ogni pallina rimasta). Trovare la % ora diventa semplice.
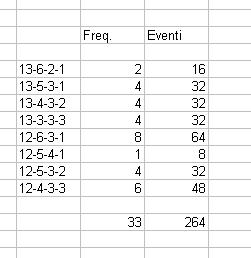
direi che parallelamente a trovare le soluzioni possibili, è necessario sapere anche quante volte possa capitare.
Ne ho trovate 33 anche se raggruppate in 8 possibili soluzioni.
Ognuna delle 33 puo' avere 8 soluzioni (una per ogni pallina rimasta). Trovare la % ora diventa semplice.



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo