Probabilità percorsi
Salve, sto cercando di calcolare la probabilità relativa ai percorsi che partono dallo stato iniziale $0$ e che portano agli stati finali $2$, $3$, $4$:
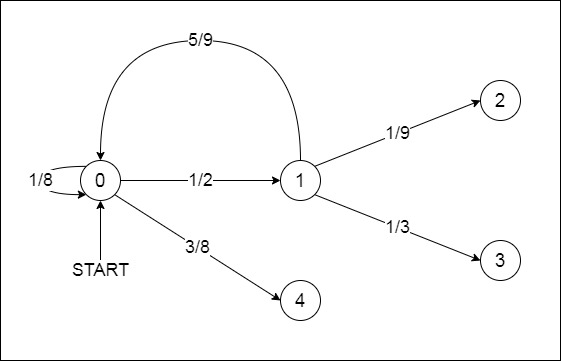
Questi i ragionamenti e i calcoli che ho fatto:
$A=sum_(n=0)^(oo)(1/8)^n=8/7$
$B=sum_(n=0)^(oo)(1/2*5/9)^n=18/13$
$p(4)=3/8[A+(B-1)+(A-1)(B-1)]=3/8*A*B=54/91$
$p(2)=1/2*1/9*A*B=8/91$
$p(3)=1/2*1/3*A*B=24/91$
Ma $p(2)+p(3)+p(4)=86/91<1$
Dove sbaglio?

Questi i ragionamenti e i calcoli che ho fatto:
$A=sum_(n=0)^(oo)(1/8)^n=8/7$
$B=sum_(n=0)^(oo)(1/2*5/9)^n=18/13$
$p(4)=3/8[A+(B-1)+(A-1)(B-1)]=3/8*A*B=54/91$
$p(2)=1/2*1/9*A*B=8/91$
$p(3)=1/2*1/3*A*B=24/91$
Ma $p(2)+p(3)+p(4)=86/91<1$
Dove sbaglio?
Risposte
Io faccio sempre così:
$H(2,2)=1$
$H(1,2)=\frac{1}{9}+\frac{5}{9}H(0,2)$
$H(0,2)=frac{1}{8}H(0,2)+\frac{1}{2}H(1,2)$
e cose simili per gli altri casi.
E tu vuoi $H(0,2)$, $H(0,3)$ e $H(0,4)$.
$H(2,2)=1$
$H(1,2)=\frac{1}{9}+\frac{5}{9}H(0,2)$
$H(0,2)=frac{1}{8}H(0,2)+\frac{1}{2}H(1,2)$
e cose simili per gli altri casi.
E tu vuoi $H(0,2)$, $H(0,3)$ e $H(0,4)$.
Grazie, credo di aver afferrato il metodo; alla fine il calcolo di $p(O',D)$, dove $O'$ e $D$ rappresentano rispettivamente il nodo di origine e di destinazione, si dovrebbe ridurre alla risoluzione di un sistema lineare (di $n$ equazioni nelle $n$ incognite $p(O_i, D)$, dove $O_i$ rappresentano gli $n$ nodi raggiungibili a partire da $O'$ e da cui è possibile raggiungere $D$), facilmente risolvibile per sostituzione.
In ogni caso, giusto per curiosità, sapreste dirmi dove ho sbagliato nel mio ragionamento iniziale?
Per esempio, in riferimento a $p(0,4)$, ho provato a sommare le probabilità relative ad ogni possibile percorso, ossia il passaggio dal nodo $0$ al nodo $4$ diretto oppure preceduto da ogni possibile combinazione di attraversamento, per un numero di volte che va da $1$ a $oo$, dei cicli (0-0) e (0-1-0). Presumo però di aver tralasciato qualcosa, visto che la probabilità trovata di $54/91$ è minore di quella corretta pari a $27/43$.
In ogni caso, giusto per curiosità, sapreste dirmi dove ho sbagliato nel mio ragionamento iniziale?
Per esempio, in riferimento a $p(0,4)$, ho provato a sommare le probabilità relative ad ogni possibile percorso, ossia il passaggio dal nodo $0$ al nodo $4$ diretto oppure preceduto da ogni possibile combinazione di attraversamento, per un numero di volte che va da $1$ a $oo$, dei cicli (0-0) e (0-1-0). Presumo però di aver tralasciato qualcosa, visto che la probabilità trovata di $54/91$ è minore di quella corretta pari a $27/43$.
"utente__medio":
Grazie, credo di aver afferrato il metodo; alla fine il calcolo di $p(O',D)$, dove $O'$ e $D$ rappresentano rispettivamente il nodo di origine e di destinazione, si dovrebbe ridurre alla risoluzione di un sistema lineare (di $n$ equazioni nelle $n$ incognite $p(O_i, D)$, dove $O_i$ rappresentano gli $n$ nodi raggiungibili a partire da $O'$ e da cui è possibile raggiungere $D$), facilmente risolvibile per sostituzione.
Le uniche destinazioni che ci interessano sono 2, 3 e 4 in questo caso. E non appariranno mai come nodi di origine per altri nodi, chiaramente.
In questo caso siamo relativamente fortunati e per ciascun problema dobbiamo usare solo 0 e 1 come origini per calcolare $H(0,n)$. In un caso più generale potrebbe essere molto peggiore. Poi guardo meglio il tuo tentativo, ma sembrava opportuno dirti che c'è questa via senza serie infinite.
Puoi anche scrivere un programma per simulare la cosa, ovviamente.
"utente__medio":
In ogni caso, giusto per curiosità, sapreste dirmi dove ho sbagliato nel mio ragionamento iniziale?
Puoi convincermi che con i tuoi $A$ e $B$ hai tenuto conto di ogni possibile successione 001001010001010101010 ecc. ?
Ovviamente se il risultato è sbagliato qualche errore ci sta... in ogni caso il ragionamento che ho fatto è il seguente:
- $3/8A$ dovrebbe tener conto del passaggio da 0 a 4 diretto o preceduto da una generica successione
di $n>=1$ (0);
- $3/8(B-1)$ dovrebbe tener conto del passaggio da 0 a 4 preceduto da una generica successione
di $n>=1$ (1-0);
- $3/8(A-1)(B-1)$ dovrebbe tener conto del passaggio da 0 a 4 preceduto da una generica combinazione di $n>=1$ (0) e (1-0).
Forse il problema è che nel terzo addendo, non tenendo conto dell'ordine con cui si susseguono gli (0) e
(1-0), vado a sottostimare il numero delle effettive successioni?
- $3/8A$ dovrebbe tener conto del passaggio da 0 a 4 diretto o preceduto da una generica successione
di $n>=1$ (0);
- $3/8(B-1)$ dovrebbe tener conto del passaggio da 0 a 4 preceduto da una generica successione
di $n>=1$ (1-0);
- $3/8(A-1)(B-1)$ dovrebbe tener conto del passaggio da 0 a 4 preceduto da una generica combinazione di $n>=1$ (0) e (1-0).
Forse il problema è che nel terzo addendo, non tenendo conto dell'ordine con cui si susseguono gli (0) e
(1-0), vado a sottostimare il numero delle effettive successioni?
"utente__medio":
Forse il problema è che nel terzo addendo, non tenendo conto dell'ordine con cui si susseguono gli (0) e
(1-0), vado a sottostimare il numero delle effettive successioni?
Perché le tue soluzioni per 2 e 3 hanno solo $AB$?
Per arrivare in uno stato finale facciamo uno di questi percorsi.
(casino)4
(casino)12
(casino)13
La tua formula per (casino) dovrebbe essere uguale in tutte e tre le risposte, se è così che vuoi procedere.
Visto che sappiamo anche che la somma delle probabilità di questi percorsi è 1 magari questo è un altro modo per arrivare alle risposte senza usare le serie infinite.
"ghira":
La tua formula per (casino) dovrebbe essere uguale in tutte e tre le risposte, se è così che vuoi procedere.
Infatti è così:
$A+(B-1)+(A-1)(B-1)=A*B$
"ghira":
Visto che sappiamo anche che la somma delle probabilità di questi percorsi è 1 magari questo è un altro modo per arrivare alle risposte senza usare le serie infinite.
Certo, anche questa potrebbe essere una strada, ma vorrei capire cosa c'è di sbagliato nel mio approccio iniziale con le serie infinite. Come detto nel precedente post:
"utente__medio":
Forse il problema è che nel terzo addendo (ossia $(A-1)(B-1)$), non tenendo conto dell'ordine con cui si susseguono gli (0) e (1-0), vado a sottostimare il numero delle effettive successioni?
Ho provato a sviluppare ulteriormente questo ragionamento, spero di non dire troppe sciocchezze...
In pratica, sempre relativamente al terzo addendo, se per una generica combinazione di (0) e (1-0) indico con $n_1$ e $n_2$ il numero di volte in cui si ripetono rispettivamente i cicli (0) e (1-0), avrò che alla suddetta combinazione corrispondono diverse successioni, il cui cui numero può essere calcolato sfruttando le permutazioni con ripetizione:
$((n_1+n_2)!)/(n_1!*n_2!)$
Ovviamente bisogna capire come tener conto di questa cosa per ogni $n_1,n_2=1,...,oo$.
Secondo voi è corretto come ragionamento?
"utente__medio":
Infatti è così:
$A+(B-1)+(A-1)(B-1)=A*B$
L'avevi anche scritto. Chiedo scusa.
"ghira":
L'avevi anche scritto. Chiedo scusa.
Figurati!
Sicuramente il metodo del "sistema lineare" è più semplice e facilmente implementabile, ma ormai mi ero intestardito di far quadrare i conti anche con le "serie infinite"... e credo di esserci riuscito!
$A=sum_(i=0)^(oo)(1/8)^i=8/7$
$B=sum_(i=0)^(oo)(1/2*5/9)^i=18/13$
$C=sum_(i=1)^(oo)[(1/8)^i*sum_(j=1)^(oo)(1/2*5/9)^j*((i+j)!)/(i!*j!)]=575/3913$
$D=A+B-1+C=72/43$
$p(0,2)=1/2*1/9*D=4/43$
$p(0,3)=1/2*1/3*D=12/43$
$p(0,4)=3/8*D=27/43$
Per quanto riguarda $C$ non so di preciso di che "animale" si tratti... mi sono limitato a darlo in pasto al buon wolfram, il quale, con mia somma sorpresa, ha restituito un risultato "umano"!
Aggiungo che non mi dispiacerebbe affatto se qualcuno che ha più dimestichezza di me con queste cose mi volesse indicare come si risolvono serie di questo tipo!
Puoi anche considerare
$a_0=1$
$a_1=\frac{1}{8}$
$a_i=\frac{1}{8}a_{i-1}+\frac{5}{18}a_{i-2}$
$a_0=1$
$a_1=\frac{1}{8}$
$a_i=\frac{1}{8}a_{i-1}+\frac{5}{18}a_{i-2}$
Mi sono reso conto che il valore di $D$, trovato al post precedente come $A+B+C-1$, può essere calcolato direttamente (e wolfram me lo conferma) come:
$D=sum_(i=0)^(oo)[(1/8)^i*sum_(j=0)^(oo)(1/2*5/9)^j*((i+j)!)/(i!*j!)]=72/43$
Nel caso in esame sul nodo $0$ insistono due percorsi ciclici, ossia (0-0), a cui è associata una probabilità di $1/8$, e (0-1-0), a cui è associata una probabilità di $1/2*5/9$; se invece i percorsi ciclici (a cui è associata una probabilità $p$) fossero tre, presumo che la formula diventerebbe:
$D=sum_(i=0)^(oo)(p_1)^i*sum_(j=0)^(oo)(p_2)^j*sum_(k=0)^(oo)(p_3)^k*((i+j+k)!)/(i!*j!*k!)$
giusto?
Nel caso fosse corretto, come si potrebbe scrivere la formula per il caso generale in cui i percorsi ciclici che insistono sul nodo siano $n$?
Infine (fatemi sapere se conviene spostare questa domanda in un'altra sezione) come andrebbero inquadrate e risolte serie di questo tipo?
$D=sum_(i=0)^(oo)[(1/8)^i*sum_(j=0)^(oo)(1/2*5/9)^j*((i+j)!)/(i!*j!)]=72/43$
Nel caso in esame sul nodo $0$ insistono due percorsi ciclici, ossia (0-0), a cui è associata una probabilità di $1/8$, e (0-1-0), a cui è associata una probabilità di $1/2*5/9$; se invece i percorsi ciclici (a cui è associata una probabilità $p$) fossero tre, presumo che la formula diventerebbe:
$D=sum_(i=0)^(oo)(p_1)^i*sum_(j=0)^(oo)(p_2)^j*sum_(k=0)^(oo)(p_3)^k*((i+j+k)!)/(i!*j!*k!)$
giusto?
Nel caso fosse corretto, come si potrebbe scrivere la formula per il caso generale in cui i percorsi ciclici che insistono sul nodo siano $n$?
Infine (fatemi sapere se conviene spostare questa domanda in un'altra sezione) come andrebbero inquadrate e risolte serie di questo tipo?
"utente__medio":
come andrebbero inquadrate e risolte serie di questo tipo?
Trasformandole in catene di Markov e calcolando i loro valori con metodi da catene di Markov?
"ghira":
ma sembrava opportuno dirti che c'è questa via senza serie infinite.
Vorrei chiedere una conferma relativamente a questo approccio (il quale si traduce nella risoluzione di $n$ sistemi lineari, uno per ogni nodo terminale raggiungibile a partire dal nodo iniziale $0$): i sistemi di equazioni così ottenuti risultano sempre determinati, giusto?
Io l'ho dedotto dal fatto che nella riduzione a scalini della matrice dei coefficienti, gli elementi della diagonale principale non possono essere mai annullati, e quindi il rango sarà sempre massimo.
"ghira":
Trasformandole in catene di Markov e calcolando i loro valori con metodi da catene di Markov?
Mi dispiace, ma è un argomento che proprio non conosco.
Ma non ci sarebbe un approccio un po' più "matematico" per risolvere serie di questo tipo?
"utente__medio":
[quote="ghira"]Trasformandole in catene di Markov e calcolando i loro valori con metodi da catene di Markov?
Mi dispiace, ma è un argomento che proprio non conosco.
[/quote]
Ma il tuo problema originale è una catena di Markov.
"ghira":
Ma il tuo problema originale è una catena di Markov.
Ah ok, buono a sapersi! In ogni caso presumo resti valida la domanda:
"utente__medio":
Ma non ci sarebbe un approccio un po' più "matematico" per risolvere serie di questo tipo?
Per quanto riguarda invece l'altra questione? Ossia:
"utente__medio":
[quote="ghira"]ma sembrava opportuno dirti che c'è questa via senza serie infinite.
Vorrei chiedere una conferma relativamente a questo approccio (il quale si traduce nella risoluzione di $ n $ sistemi lineari, uno per ogni nodo terminale raggiungibile a partire dal nodo iniziale $ 0 $): i sistemi di equazioni così ottenuti risultano sempre determinati, giusto?[/quote]
"utente__medio":
Ma non ci sarebbe un approccio un po' più "matematico" per risolvere serie di questo tipo?
Come dice Ghira, è una catena di Markov...ed è intuibile che nel luuuuungo periodo tutto si arresti in uno dei nodi 2,3 o 4.
Per problemi discreti, come questo, il miglior metodo è l'algebra lineare. Si trasforma il grafo in una matrice:
$ M=( ( 1/8 , 5/9 , 0 , 0 , 0 ),( 1/2 , 0 , 0 , 0 , 0 ),( 0 , 1/9 , 1 , 0 , 0 ),( 0 , 1/3 , 0 , 1 , 0 ),( 3/8 , 0 , 0 , 0 , 1 ) ) $
(è facile, è come battaglia navale e noterai che ogni colonna somma a 1. Sul significato, magari ne parliamo quando avrai risposta alla domanda sotto).
M è la matrice di transizione. Diagonalizzandola, e usando una proprietà fondamentale, è possibile ottenere la matrice di convergenza "ad infinitum" :
$ M^(oo)=( ( 0 , 0 , 0 , 0 , 0 ),( 0 , 0 , 0 , 0 , 0 ),( 4/43 , 7/43 , 1 , 0 , 0 ),( 12/43 , 21/43 , 0 , 1 , 0 ),( 27/43 , 15/43 , 0 , 0 , 1 ) ) $
Questa matrice ci dice che partendo dai nodi 2, 3 o 4, si finisce/resta in quei nodi con probabilità 1 (come è ovvio che sia dato che non si può uscirne).
Partendo invece dal nodo 0, si finirà nel nodo 2 con prob. 4/43, ovvero $P_0(2)=4/43$
Poi abbiamo $P_0(3)=12/43$ e $P_0(4)=27/43$. Se sommate danno ovviamente 1.
Partendo dal nodo 1 invece abbiamo $P_1(2)=7/43$, $P_1(3)=21/43$ e infine $P_1(4)=15/43$
Conosci l'algebra lineare?
"Bokonon":
Conosci l'algebra lineare?
Ciao, in realtà dopo la prima risposta di ghira al topic:
"ghira":
Io faccio sempre così:
$H(2,2)=1$
$H(1,2)=\frac{1}{9}+\frac{5}{9}H(0,2)$
$H(0,2)=frac{1}{8}H(0,2)+\frac{1}{2}H(1,2)$
e cose simili per gli altri casi.
E tu vuoi $H(0,2)$, $H(0,3)$ e $H(0,4)$.
pur non conoscendo le catene di Markov, ho subito provveduto ad implementare quello che nei precedenti post ho chiamato "metodo del sistema lineare". In pratica a partire da una matrice $A$ di dimensioni $nXn$ (quasi equivalente a quella che tu chiami "matrice di transizione") fornita dal problema (il grafo l'ho ricavato io)
$A=((1, 4, 0, 0, 3),(5, 0, 1, 3, 0),(0, 0, 0, 0, 0),(0, 0, 0, 0, 0),(0, 0, 0, 0, 0))$
ho ricavato una seconda matrice $B$ di valori booleani, delle stesse dimensioni di $A$, dove il generico elemento $e_(ij)$ indica se dal nodo $i$-esimo è possibile o meno raggiungere il nodo $j$-esimo.
A questo punto, a partire da $A$ e $B$, risulta abbastanza agevole ricavare per ogni stato terminale ($2,3,4$ in questo caso) una matrice $C$ di dimensioni $nX(n+1)$ contenente i coefficienti di un sistema lineare come quello riportato nel messaggio quotato sopra.
Quindi per risolvere il sistema, o meglio per ottenere $p(0,"nodo terminale")$, che poi è quello che mi interessa, ho ridotto $C$ a scalini e annullato gli elementi extra-diagonali relativi alla prima riga.
Detto ciò, l'approccio da te utilizzato mi sembra molto interessante, ma di preciso come si passa dalla matrice "di transizione" a quella "di convergenza"? Se è troppo lungo o complicato da spiegare non ti preoccupare, farò poi io qualche ricerca in rete sulle catene di Markov.
In ogni caso penso che permangono le due domande fatte in precedenza:
- sistemi di equazioni come quelli appena descritti (che si traducono nella matrice $C$) risultano sempre determinati? Da un ragionamento veloce mi verrebbe da dire di sì, in quanto gli elementi della diagonale principale non possono essere annullati e quindi il rango di $C$ sarà sempre massimo, ma non ne sono sicuro;
- come andrebbero inquadrate e risolte serie di questo tipo:
$D=sum_(i=0)^(oo)(p_1)^isum_(j=0)^(oo)(p_2)^j((i+j)!)/(i!*j!)$ con $p in(0,1)$
"utente__medio":
Detto ciò, l'approccio da te utilizzato mi sembra molto interessante, ma di preciso come si passa dalla matrice "di transizione" a quella "di convergenza"?
Se non erro, hai capito come ho costruito la matrice di transizione M: quindi do questo passaggio per assodato.
(Nota a parte: a me piace lavorare per colonne mentre invece spesso e volentieri in letteratura lavorano per righe...questioni di gusti, ma il mio è migliore
 )
)Non ho inventato le matrici di transizione di stato (oppure matrici di Markov o semplicemente matrici stocastiche) e non gli ho neppure dato il nome: https://en.wikipedia.org/wiki/Stochastic_matrix
Come funzionano? Semplice, si moltiplica la matrice per lo stato iniziale e poi si opera ricorsivamente.
Se immaginiamo di mettere una biglia nel grafo (che è un percorso aleatorio), $Ms_0=s_1$
$s_0$ è lo stato iniziale della biglia: per esempio, nel nostro esempio, $s_0^T=(1,0,0,0,0)^T$ equivale a dire ho posto la biglia con certezza nel nodo 0. Oppure $s_0^T=(1/5,1/5,1/5,1/5,1/5)^T$ equivale a dire ho lanciato bendato la biglia a caso in uno dei possibili stati iniziali
$s_1$ è il vettore che rappresenta lo stato aleatorio della biglia dopo la prima iterazione (oppure dopo la prima transizione temporale fissa).
$Ms_0=s_2$ è lo stato/distribuzione aleatoria dopo la seconda transizione e così via $Ms_(n-1)=s_n$
Niente di complicato insomma: per esempio $ M( ( 1 ),( 0 ),( 0 ),( 0 ),( 0 ) ) $ restituisce la prima colonna di M.
Ora poichè $s_n=Ms_(n-1)=M^2s_(n-2)=...=M^ns_0$ significa che, stabilito lo stato iniziale, siamo solo interessati alle potenze della matrice di transizione.
Come è noto, SE la matrice è diagonalizzabile (altrimenti si passa alla forma canonica di Jordan etc etc...ma restiamo sul semplice), allora abbiamo che $M=SDS^(-1)$ per cui $M*M=M^2=SDS^(-1)SDS^(-1)=SD^2S^(-1)$ e così via ricorsivamente ottenendo $M^n=SD^nS^(-1)$.
La diagonalizzazione semplifica i calcoli di $M^n$ perchè, una volta nota la matrice degli autovettori, è sufficiente calcolare le potenze della matrice diagonale degli autovalori, ovvero elevare all'ennesima potenza ogni elemento della diagonale tout court. A livello pratico, questo rende assai più facile calcolare $M^ns_0=s_n$ (ammesso che calcolare la matrice degli autovettori e la sua inversa sia una cosa "facile"...ma a questo vengono incontro gli algoritmi numerici).
Inoltre, la teoria ci assicura che i valori assoluti degli autovalori di una matrice di transizione diagonalizzabile siano tutti compresi fra $0<|d_i|<=1$.
Un autovalore pari ad 1 è sempre associato alla colonna della matrice di transizione che corrisponde ad un nodo senza uscita (nel nostro esempio infatti le ultime tre colonne di M sono tutti nodi senza uscita e sono appunto autovettori associato al medesimo autospazio).
Tornando al nostro esempio, sappiamo già che (fissato uno stato iniziale) nel lungo periodo la nostra biglia entrerà (senza mai più uscirne) in tre possibili stati. E quindi sappiamo anche che la nostra $D$ ha tre $1$ sulla diagonale e due valori compresi fra -1 e 1.
Sorprendentemente $1^n=1$ sempre

Mentre se si eleva $0<|d_i|<=1$ abbiamo che $lim_(n->oo) d_i^n =0$.
Ergo, $lim_(n->oo) D^n=D^(oo)$ restituisce la nostra matrice diagonale in cui sono rimasti solo gli $1$ sulla diagonale e il resto è tutto zero.
Pertanto $lim_(n->oo) M^n =M^(oo)=SD^(oo)S^(-1)$
Ed è così che ho calcolato la matrice a cui converge: per il resto basta fare $M^(oo)s_0$ e si ottiene tutto ciò che vogliamo sapere. Inoltre possiamo calcolare rapidamente anche $M^(20)( ( 1 ),( 0 ),( 0 ),( 0 ),( 0 ) )$ e scoprire che alla 20-esima transizione la probabilità che la biglia, partita dal nodo $0$, si trovi nel nodo $0$ oppure nel nodo $1$ è di circa 1/50.000.
Ora, io intendevo solo darti un'infarinatura sulle matrici di Markov. Tutta la parte teorica la trovi nei libri (in cui vengono spiegate anche le convergenze o meno del processo stocastico in tutte le sue variegate possibili forme).
Per quanto riguarda il tuo approccio, mi spiace ma è confuso e non vale la pena che tu ci spenda tempo.
"Bokonon":
Ora, io intendevo solo darti un'infarinatura delle matrici di Markov. Tutta la parte teorica la trovi nei libri (in cui vengono spiegate anche le convergenze o meno del processo stocastico in tutte le sue variegate possibili forme).
In linea di massima ho capito il procedimento, ma ovviamente si tratta di argomenti che vanno studiati per bene; in ogni caso grazie mille per l'infarinatura!
"Bokonon":
Per quanto riguarda il tuo approccio, mi spiace ma è confuso e non vale la pena che tu ci spenda tempo.
Se ti riferisci all'approccio matriciale che ho esposto nel precedente messaggio, purtroppo il consiglio viene fuori tempo massimo, in quanto l'ho già implementato; inoltre sinceramente mi sembra un approccio molto "accessibile", in quanto basato su logica e algebra lineare di base.
Se ti riferisci invece all'approccio basato sulle serie infinite, in effetti risulta un po' più complesso e contorto, ma ci ho ragionato molto e alla fine credo di aver trovato il modo di formalizzare il problema correttamente (se volete posso spiegare meglio l'algoritmo risolutivo). Inoltre visto che ho già implementato tutto e che manca solo una soluzione in forma chiusa (ammesso che esista) per serie del tipo postato in precedenza, mi sembra un peccato non andare fino in fondo, in modo poi da poter anche confrontare l'efficienza tra i vari approcci.
"utente__medio":
In linea di massima ho capito il procedimento, ma ovviamente si tratta di argomenti che vanno studiati per bene; in ogni caso grazie mille per l'infarinatura!
Per fare un esempio concreto, puoi risolvere questo problema in due righe con le catene di Markov:
"Se un cavallo degli scacchi si muove a caso (cioè sceglie uniformemente fra le mosse possibili in ogni momento) e adesso si trova sulla casella A1, mediamente fra quante mosse si troverà di nuovo su A1?"
e la seconda di queste due righe è "=168" (se mi ricordo bene). Ok ho fatto il calcolo. 168.
E lo stesso per la una torre, un re, una donna. Solo che i numeri sono diversi. Per la torre la risposta è "ovviamente" 64.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo