Probabilità con 40 carte ...
Salve ragazzi, un amico parlando di giochi di carte è entrato in discorso con un gioco eseguito con le 40 classiche carte e dice che distribuendo 3 carte all'avversario e 3 carte a lui, basandosi su una regola che se il mazziere abbia fra le sue 3 carte una uguale fra le 3 dell'avversario, vince; dice che il mazziere ha un vantaggio sempre maggiore .
Esiste un calcolo matematico per vedere se è veramente cosi ?
Semplifico:
avendo un mazzo di 40 carte che vanno dall'Asso al RE e distribuendo due gruppi di 3 carte a terra, quante probabilità ci sono che nei due gruppi esca una carta uguale ?
Naturalmente le carte vengono distribuite sempre nello stesso modo, cioè, mischiata, alzata, distribuzione delle prime 3 carte all'avevrsario e distibuzione delle seconde 3 carte al mazziere.
Grazie.
Esiste un calcolo matematico per vedere se è veramente cosi ?
Semplifico:
avendo un mazzo di 40 carte che vanno dall'Asso al RE e distribuendo due gruppi di 3 carte a terra, quante probabilità ci sono che nei due gruppi esca una carta uguale ?
Naturalmente le carte vengono distribuite sempre nello stesso modo, cioè, mischiata, alzata, distribuzione delle prime 3 carte all'avevrsario e distibuzione delle seconde 3 carte al mazziere.
Grazie.
Risposte
Scusa, ma non ho compreso se le carte uguali devono essere all'interno delle 3 carte del mazziere o se una delle 3 carte del mazziere deve essere uguale ad una delle 3 carte dell'avversario.
Per carte uguali intendi ad es. 4 di picche con 4 di fiori o ad es. re di cuori con re di quadri?
Per carte uguali intendi ad es. 4 di picche con 4 di fiori o ad es. re di cuori con re di quadri?
Esatta la seconda ipotesi:
se il mazziere ha una carta uguale ad una delle 3 dell'avversario, vince.
può verificarsi anche la possibilità che l'avversario riceve 3 carte uguali e il mazziere prende la 4° mancante, vincendo.
se il mazziere ha una carta uguale ad una delle 3 dell'avversario, vince.
può verificarsi anche la possibilità che l'avversario riceve 3 carte uguali e il mazziere prende la 4° mancante, vincendo.
"danut":
Salve ragazzi, un amico parlando di giochi di carte è entrato in discorso con un gioco eseguito con le 40 classiche carte e dice che distribuendo 3 carte all'avversario e 3 carte a lui, basandosi su una regola che se il mazziere abbia fra le sue 3 carte una uguale fra le 3 dell'avversario, vince; dice che il mazziere ha un vantaggio sempre maggiore .
Esiste un calcolo matematico per vedere se è veramente cosi ?
Semplifico:
avendo un mazzo di 40 carte che vanno dall'Asso al RE e distribuendo due gruppi di 3 carte a terra, quante probabilità ci sono che nei due gruppi esca una carta uguale ?
Naturalmente le carte vengono distribuite sempre nello stesso modo, cioè, mischiata, alzata, distribuzione delle prime 3 carte all'avevrsario e distibuzione delle seconde 3 carte al mazziere.
Grazie.
Allora...
Secondo me la probabilità che nei due gruppi di 3 carte ci sia una carta uguale è:
$P=(4*((9),(4))*10*((4),(2)))/(((40),(6)))$.
Questo risultato perchè...
Intanto è come estrarre 6 carte da un mazzo di 40.
Per quanto riguarda il numeratore, è possibile ottenere $10*((4),(2))$ insiemi di due carte uguali. Successivamente ogni combinazione di due carte uguali deve avere le rimanenti 4 diverse cioè $((9),(4))*4$. Ho moltiplicato per $4$ perchè tengo conto del tipo (quadri, cuori, fiori, picche).
Grazie clrscr, ma ci ho capito poco 
quindi qual'è la percentuale che il mazziere vince sull'avversario ?
quindi qual'è la percentuale che il mazziere vince sull'avversario ?
"danut":
Grazie clrscr, ma ci ho capito poco
quindi qual'è la percentuale che il mazziere vince sull'avversario ?
Più o meno il $0.7%$. Spero di non aver sbagliato...
Volevo dire un' ultima cosa...
La probabilità calcolata è la probabilità di vincita del mazziere quando per vittoria si intende che ci sia SOLO UNA COPPIA di carte uguali...
Però se la vittoria corrispondesse al fatto che ci sia ALMENO una coppia uguale, allora il risultato sarebbe molto diverso...
La probabilità calcolata è la probabilità di vincita del mazziere quando per vittoria si intende che ci sia SOLO UNA COPPIA di carte uguali...
Però se la vittoria corrispondesse al fatto che ci sia ALMENO una coppia uguale, allora il risultato sarebbe molto diverso...
"clrscr":
[quote="danut"]Grazie clrscr, ma ci ho capito poco
quindi qual'è la percentuale che il mazziere vince sull'avversario ?
Più o meno il $0.7%$. Spero di non aver sbagliato...[/quote]
0,7 % ?
mi sembra un po pochino.... cosi' a sensazione !!!
0.7 ?
penso anche io che sia un po poco !
in questo caso una coppia di carte uscirebbe 7 volte ogni 1000, e facendo delle prove reali, anche se so che poche prove non bastano per determinarlo, il risultato è largamente superiore.
penso anche io che sia un po poco !
in questo caso una coppia di carte uscirebbe 7 volte ogni 1000, e facendo delle prove reali, anche se so che poche prove non bastano per determinarlo, il risultato è largamente superiore.
Da una prima indagine sembra effettivamente che il mazziere abbia più probabilità di vincita!
I dati elaborati dicono di: 52,9 % (circa) di vincita e 47,1 % (circa) di perdita.
I dati elaborati dicono di: 52,9 % (circa) di vincita e 47,1 % (circa) di perdita.
Grazie Umby per il tuo contributo, potresti gentilmente scrivere il calcolo che hai eseguito per arrivare a questo risultato ?
Ti ringrazio
Ti ringrazio
Tengo a precisare che il calcolo non l'ho fatto io, ma il mio pc. 
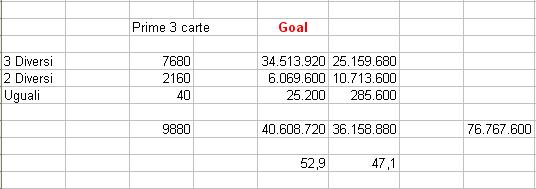
Comunque ho simulato il primo lancio delle 3 carte $(40*39*38)/(3*2)=9880$ ed ho calcolato le possibilita' che queste 3 carte siano tutte le 3 diverse tra loro, oppure due diverse, oppure tutte le 3 uguali, e per ognuna di queste possibilità ho calcolato $(37*36*35)/(3*2)=7770$ (successive 3 carte).
Mi sembra ovvio che se le prime 3 carte sono tutte diverse, la percentuale che una delle altre 3 sia uguale è piu alta (vedi prima riga).
Cmq, su 76 milioni di possibilità, 40 milioni sono quelle favorevoli (vedi colonna Goal)
Spero di aver preso in esame tutto, e che non mi sia sfuggito nulla.

Comunque ho simulato il primo lancio delle 3 carte $(40*39*38)/(3*2)=9880$ ed ho calcolato le possibilita' che queste 3 carte siano tutte le 3 diverse tra loro, oppure due diverse, oppure tutte le 3 uguali, e per ognuna di queste possibilità ho calcolato $(37*36*35)/(3*2)=7770$ (successive 3 carte).
Mi sembra ovvio che se le prime 3 carte sono tutte diverse, la percentuale che una delle altre 3 sia uguale è piu alta (vedi prima riga).
Cmq, su 76 milioni di possibilità, 40 milioni sono quelle favorevoli (vedi colonna Goal)
Spero di aver preso in esame tutto, e che non mi sia sfuggito nulla.

Umby, mi sembra che non ti è sfuggito nulla, oppure ho fatto anch'io lo stesso errore.
Ho fatto un giro diverso per arrivare al risultato, che però risulta uguale.
Ho preso in esame i 3 casi (carte avversario= 1° caso 3 carte uguali
2° caso 2 carte uguali
3° caso 3 carte diverse
Per ogni caso ho calcolato le % di uscita delle 3 carte e le % di vincita del mazziere
1° caso - probabiltà di uscita di 3 carte uguali = 0,4048%
probabiltà di vincita del mazziere 630 contro 7140 di perdere =8,1081%
percentuale totale = 0,0328%
2° caso probabiltà di uscita di 2 carte uguali = 21,8623%
probabiltà di vincita del mazziere 2810 contro 4960 di perdere =36,1647%
percentuale totale = 7,9064%
3° caso probabiltà di uscita di 3 carte diverse = 77,7327%
probabiltà di vincita del mazziere 4494 contro 3276 di perdere =57,8378%
percentuale totale = 44,9588%
Sommando le % totali si ricava:
0,0328+7.9064+44.9588= 52,898%
Ho fatto un giro diverso per arrivare al risultato, che però risulta uguale.
Ho preso in esame i 3 casi (carte avversario= 1° caso 3 carte uguali
2° caso 2 carte uguali
3° caso 3 carte diverse
Per ogni caso ho calcolato le % di uscita delle 3 carte e le % di vincita del mazziere
1° caso - probabiltà di uscita di 3 carte uguali = 0,4048%
probabiltà di vincita del mazziere 630 contro 7140 di perdere =8,1081%
percentuale totale = 0,0328%
2° caso probabiltà di uscita di 2 carte uguali = 21,8623%
probabiltà di vincita del mazziere 2810 contro 4960 di perdere =36,1647%
percentuale totale = 7,9064%
3° caso probabiltà di uscita di 3 carte diverse = 77,7327%
probabiltà di vincita del mazziere 4494 contro 3276 di perdere =57,8378%
percentuale totale = 44,9588%
Sommando le % totali si ricava:
0,0328+7.9064+44.9588= 52,898%
Bene, mi fa piacere vedere che si è giunto allo stesso risultato, percerrendo una altra strada ! 


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo