Non riesco a fare un grafico....
Ciao devo fare un grafico sulla densità di una determinata tabella. Ma quando vado su exel per fare il mio grafico, non so come inserire i dati x far uscire la tabella come la voglio io; ho provato centinaia di volte ma non mi viene.....potete consigliarmi......???......grazie..... 
Risposte
altre info ?
cerca di essere piu dettagliata....
cerca di essere piu dettagliata....
Che significa "densità di una tabella"? Mai sentito un'espressione così vaga!
Sono tuttavia pieno d'ammirazione per quel "centinaia di volte" che la dice tutta sulla tenacia di Babygirl.
Lo stesso Vittorio Alfieri, ben noto per il suo "volli, volli, volli, fortissimamente volli", lei fa appena un baffo!
Sono tuttavia pieno d'ammirazione per quel "centinaia di volte" che la dice tutta sulla tenacia di Babygirl.
Lo stesso Vittorio Alfieri, ben noto per il suo "volli, volli, volli, fortissimamente volli", lei fa appena un baffo!
in un esercizio di statistica mi sono calcolata l'ampiezza, le frequenze percentuali ed infine la relativa densità. L'esercizio mi chiede di fare anche una rappresentazione grafica, attraverso stogramma, di questi dati, ma non riesco a fare il grafico.
seleziona un po di dati ( a titolo di esempio), ed allegali a questa discussione.
i miei dati sono :
Voto test---------Ampiezza------fp (%)--------Densità
14 - 17__________3_________5___________1,666
17 - 23__________6_________30__________5
23 - 27_________ 4_________54__________13,5
27 - 30 _________ 3_________11__________3,666
adesso con qst dati devo fare il mio grafico.....
Voto test---------Ampiezza------fp (%)--------Densità
14 - 17__________3_________5___________1,666
17 - 23__________6_________30__________5
23 - 27_________ 4_________54__________13,5
27 - 30 _________ 3_________11__________3,666
adesso con qst dati devo fare il mio grafico.....
Fer fare uno "stogramma" occorre procedere come segue.
Nel seguito assumo che i tuoi dati provengano da una variabile aleatoria continua e che i dati siano almeno 30.
Innanzi tutto devi fissare un certo numero di classi, di norma ugualmente ampie.
Per esempio, se hai 120 dati che oscillano fra -3 e 5, puoi fissare anche una ventina di classi (5 punti in media per ogni classe). Per fissare le classi dividi l'intervallo fra minimo (-3) e massimo (5) in 20 parti (dette anche classi o "bin"). A questo punto devi contare le frequenze assolute per ogni bin, cioè quanti dei tuoi dati cadono in ogni bin.
Alla fine avrai per esempio:
_____Bin______Conteggi
da -3 a -2.5_______ 7
da -2.5 a -2_______18
......
da 4.5 a 5.0 _______ 3
Quelle che ho chiamato conteggi (o "frequenze assolute" dello "stogramma") sono le altezze delle barre rettangolari che, disegnate sopra ogni bin a partire dall'asse x, vanno a formare, appunto, il cosiddetto 'sto gramma.
Ma, per avere una migliore presentazione conviene a questo punto disegnare non le frequenze assolute, bensì quelle percentuali, che si ottengono dalle assolute dividendo per il numero totale di dati e moltiplicando per 100.
Per esempio se hai 120 dati e in un bin ne cadono 18, allora 18 è la frequenza assoluta, mentre la frequenza relativa è: $100 xx (18/120) = 15%$
Se si disegna appunto lo sto-gramma usando le frequenze percentuali, si ha una rappresentazione sperimentale efficace di quella che è la sottostante densità di probabilità della variabile aleatoria che è stata campionata (di cui cioè si sono osservati quei 120 dati di cui si parlava).
Chiaro?
Nel seguito assumo che i tuoi dati provengano da una variabile aleatoria continua e che i dati siano almeno 30.
Innanzi tutto devi fissare un certo numero di classi, di norma ugualmente ampie.
Per esempio, se hai 120 dati che oscillano fra -3 e 5, puoi fissare anche una ventina di classi (5 punti in media per ogni classe). Per fissare le classi dividi l'intervallo fra minimo (-3) e massimo (5) in 20 parti (dette anche classi o "bin"). A questo punto devi contare le frequenze assolute per ogni bin, cioè quanti dei tuoi dati cadono in ogni bin.
Alla fine avrai per esempio:
_____Bin______Conteggi
da -3 a -2.5_______ 7
da -2.5 a -2_______18
......
da 4.5 a 5.0 _______ 3
Quelle che ho chiamato conteggi (o "frequenze assolute" dello "stogramma") sono le altezze delle barre rettangolari che, disegnate sopra ogni bin a partire dall'asse x, vanno a formare, appunto, il cosiddetto 'sto gramma.
Ma, per avere una migliore presentazione conviene a questo punto disegnare non le frequenze assolute, bensì quelle percentuali, che si ottengono dalle assolute dividendo per il numero totale di dati e moltiplicando per 100.
Per esempio se hai 120 dati e in un bin ne cadono 18, allora 18 è la frequenza assoluta, mentre la frequenza relativa è: $100 xx (18/120) = 15%$
Se si disegna appunto lo sto-gramma usando le frequenze percentuali, si ha una rappresentazione sperimentale efficace di quella che è la sottostante densità di probabilità della variabile aleatoria che è stata campionata (di cui cioè si sono osservati quei 120 dati di cui si parlava).
Chiaro?
Si ho capito e ti ringrazio per la risposta. Non so se hai visto i miei dati che ho aggiunto poco fa. In base hai quei dati, come posso fare per creare un grafico?....non so se hai capito cosa intendo....io una volta calcolata la densità di una variabile aleatoria, devo rappresentare la stessa attraverso un grafico....ma non lo so fare
Il primo che farei è la rappresentazione delle % (ti consiglio la torta per le % perchè rende bene visivamente)...
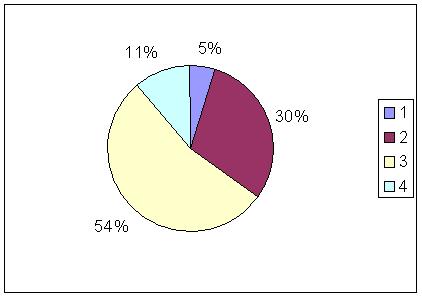

@BabyGirl
Non avevo letto la tua risposta a Umby.
Ora ho visto i tuoi dati e ho anche visto che i tuoi bin non sono tutti ugualmente ampi.
Mancano le frequenze assolute, ma fa niente.
I calcoli sono ben fatti.
Per fare ora il cosiddetto "stogramma", disegna su ogni bin un rettangolo alto quanto la rispettiva densità.
Avrai così una rappresentazione efficace della sottostante densità di probabilità (come dicevo nel mio precedente intervento).
Per esempio, sul secondo bin (che va da 17 a 23) devi disegnare un rettangolo appoggiato sull'asse $x$ di base 6 (cioè pari all'ampiezza del bin) e di altezza 5 (pari cioè alla rispettiva densità).
Chiaro?
Non avevo letto la tua risposta a Umby.
Ora ho visto i tuoi dati e ho anche visto che i tuoi bin non sono tutti ugualmente ampi.
Mancano le frequenze assolute, ma fa niente.
I calcoli sono ben fatti.
Per fare ora il cosiddetto "stogramma", disegna su ogni bin un rettangolo alto quanto la rispettiva densità.
Avrai così una rappresentazione efficace della sottostante densità di probabilità (come dicevo nel mio precedente intervento).
Per esempio, sul secondo bin (che va da 17 a 23) devi disegnare un rettangolo appoggiato sull'asse $x$ di base 6 (cioè pari all'ampiezza del bin) e di altezza 5 (pari cioè alla rispettiva densità).
Chiaro?
Ok ci provo.....ti ringrazio...!!!
Cmq grazie a tutti..... 


Io invece di una "torta" (in gergo, "pie-plot") ti consiglio invece un'umile rappresentazione con 4 rettangoli in severo black & white, anche perchè nessuno considererebbe seriamente uno stogramma una "torta", per quanto attraente e squisita sia!
Ve detto che anche l'istogramma presenta alcuni problemi di soggettività. Se non mi sbaglio, ultimamente si cerca di risolvere il problema utilizzando l'istogramma perequato, la cui opzione dovrebbe essere presente in quasi tutti i software (ovviamente free, sono da preferirsi per ovvi motivi  ).
).
 ).
).
Permettimi di dissentire.
Innanzi tutto non vedo quali problemi di "soggettività" possa presentare un istogramma che non si presentino anche con una torta.
La torta ha poi un grave difetto che l'istogramma non ha: congiungendo in modo circolare l'ultimo bin col primo, si finisce per perdere la serialità dei bin e quindi anche una quantità importante di informazioni circa la distribuzione di probabilità, cioè per esempio in quali intervalli tale densità è una funzione crescente e in quali decrescente, dove tende ad essere concava e in quali convessa, etc.... Vi sembra poco?
A mio parere, l'unica soggettività insita in un istogramma è la scelta dei bin (o classi), ma in questo un istogranna non ha nulla da invidiare ad una torta!
Innanzi tutto non vedo quali problemi di "soggettività" possa presentare un istogramma che non si presentino anche con una torta.
La torta ha poi un grave difetto che l'istogramma non ha: congiungendo in modo circolare l'ultimo bin col primo, si finisce per perdere la serialità dei bin e quindi anche una quantità importante di informazioni circa la distribuzione di probabilità, cioè per esempio in quali intervalli tale densità è una funzione crescente e in quali decrescente, dove tende ad essere concava e in quali convessa, etc.... Vi sembra poco?
A mio parere, l'unica soggettività insita in un istogramma è la scelta dei bin (o classi), ma in questo un istogranna non ha nulla da invidiare ad una torta!
Figurati, puoi dissentire tranquillamente. Il mio intervento non era per evidenziare che la "torta" fosse meglio dell'istogramma: ho voluto evidenziare che anche l'istogramma presenta alcuni problemi, come la scelta delle classi (che non è poco e non è l'unico). Anche io preferisco l'istogramma alla "torta", ma preferisco anche l'istogramma perequato all'istogramma "classico"  .
.
 .
.
E io l'istogramma "fuzzy" ...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo