Interpretazione malata testo
Poker italiano (32 carte). Sapendo che il vostro vicino di destra ha un poker di assi ed un re e quello di sinistra un tris di re, qual è la probabilità di fare un tris di donne?
Ora, interpretandolo normalmente la probabilità viene $(((4),(3))*((20),(2)))/(((24),(4)))$
Se però lo intendo che il giocatore di sinistra ha un tris di re e solo un tris di re, cioè non può avere un full, la probabilità dovrebbe cambiare... infatti, se lo intendo nel primo modo è possibile che abbia una coppia di donne, mentre la secodna interpretazione esclude questo caso, per cui la probabilità deve essere diversa. (e non credo che sia solo questo il caso in cui cambi la probabilità da calcolare...).
Ora, interpretandolo normalmente la probabilità viene $(((4),(3))*((20),(2)))/(((24),(4)))$
Se però lo intendo che il giocatore di sinistra ha un tris di re e solo un tris di re, cioè non può avere un full, la probabilità dovrebbe cambiare... infatti, se lo intendo nel primo modo è possibile che abbia una coppia di donne, mentre la secodna interpretazione esclude questo caso, per cui la probabilità deve essere diversa. (e non credo che sia solo questo il caso in cui cambi la probabilità da calcolare...).
Risposte
"nato_pigro":
Poker italiano (32 carte). Sapendo che il vostro vicino di destra ha un poker di assi ed un re e quello di sinistra un tris di re, qual è la probabilità di fare un tris di donne?
Ora, interpretandolo normalmente la probabilità viene $(((4),(3))*((20),(2)))/(((24),(4)))$
Se però lo intendo che il giocatore di sinistra ha un tris di re e solo un tris di re, cioè non può avere un full, la probabilità dovrebbe cambiare... infatti, se lo intendo nel primo modo è possibile che abbia una coppia di donne, mentre la secodna interpretazione esclude questo caso, per cui la probabilità deve essere diversa. (e non credo che sia solo questo il caso in cui cambi la probabilità da calcolare...).
Secondo me a occhio invece la probabilità potrebbe rimanere la stessa, perchè così come escludi la coppia di donne escludi anche la coppia di qualsiasi altro valore.
(Comunque il denominatore dovrebbe essere $((24),(5))$
si, ma la probabilità che ci interessa è il tris di donne. Secondo la prima interpretazione, qualunque siano le due carte restanti del giocatore è possibile per me fare il tris di donne. Con la seconda se l'altro ha full con coppia di donne io non sono più in grado di fare il tris. Mi sembra una differenza notevole...
In caso potresti chiamare $F_i =$ {Il giocatore di sinistra ha $i$ donne}
e calcolare $P(E) = P(E|F_0)P(F_0) + P(E|F_1)P(F_1) + P(E|F_2)P(F_2)$.
E' vero che può capitare che il giocatore di sinistra abbia due donne, ma la probabilità non è altissima.
Edit: Nel caso i risultati non coincidano, comunque, a modificare la tua formula è l'ipotesi che il giocatore non possa avere full: nel caso egli possa avere due carte qualsiasi, ciò equivale a togliere due carte a caso dal mazzo (il che quindi non modificherebbe la probabilità richiesta).
e calcolare $P(E) = P(E|F_0)P(F_0) + P(E|F_1)P(F_1) + P(E|F_2)P(F_2)$.
E' vero che può capitare che il giocatore di sinistra abbia due donne, ma la probabilità non è altissima.
Edit: Nel caso i risultati non coincidano, comunque, a modificare la tua formula è l'ipotesi che il giocatore non possa avere full: nel caso egli possa avere due carte qualsiasi, ciò equivale a togliere due carte a caso dal mazzo (il che quindi non modificherebbe la probabilità richiesta).
"Gatto89":
In caso potresti chiamare $F_i =$ {Il giocatore di sinistra ha $i$ donne}
e calcolare $P(E) = P(E|F_0)P(F_0) + P(E|F_1)P(F_1) + P(E|F_2)P(F_2)$.
E' vero che può capitare che il giocatore di sinistra abbia due donne, ma la probabilità non è altissima.
nè ma non è questione se la probabilità è alta o bassa. la questione è "qual è questa probabilità"...
"Gatto89":
Edit: Nel caso i risultati non coincidano, comunque, a modificare la tua formula è l'ipotesi che il giocatore non possa avere full: nel caso egli possa avere due carte qualsiasi, ciò equivale a togliere due carte a caso dal mazzo (il che quindi non modificherebbe la probabilità richiesta).
non ho ben capito...
Riprendendo il calcolo:
La formula $(((4),(3))*((20),(2)))/(((24),(5)))$ pari a 1,788% mi determina la possibilita' che escano le 3 donne
La stessa include anche eventuali full (le 3 donne appunto, con una coppia)
La possibilita' di questa coppia è pari a $3/19$ (escludendo la quarta donna, restano 20 carte, mettendo una qualsiasi in quarta posizione, ne restano 3 su 19 dello stesso valore), quindi otteniamo:
$(((4),(3))*((20),(2)))/(((24),(5))) * 16/19$ pari al 1,506%
.... manca l'ultimo passaggio (il giocatore alla mia sinistra NON ha un full....)
La formula $(((4),(3))*((20),(2)))/(((24),(5)))$ pari a 1,788% mi determina la possibilita' che escano le 3 donne
La stessa include anche eventuali full (le 3 donne appunto, con una coppia)
La possibilita' di questa coppia è pari a $3/19$ (escludendo la quarta donna, restano 20 carte, mettendo una qualsiasi in quarta posizione, ne restano 3 su 19 dello stesso valore), quindi otteniamo:
$(((4),(3))*((20),(2)))/(((24),(5))) * 16/19$ pari al 1,506%
.... manca l'ultimo passaggio (il giocatore alla mia sinistra NON ha un full....)
Opps... ho cancelllato un mio intervento per errore. Sorry... 
rimane ancora da fare l'ultimo step ....

rimane ancora da fare l'ultimo step ....
"nato_pigro":
... infatti, se lo intendo nel primo modo è possibile che abbia una coppia di donne, mentre la secodna interpretazione esclude questo caso....
"Gatto89":
E' vero che può capitare che il giocatore di sinistra abbia due donne, ma la probabilità non è altissima.
Il giocatore alla mia sinistra NON puo' avere una coppia di donne. Nel senso che la formula applicata ci determina la possibilità che io abbia 3 ( e solo 3 [nemmeno 4]) donne. Quindi ne rimane un'altra, che potrebbe o non potrebbe avere il mio compagno.
"Umby":
[quote="nato_pigro"]
... infatti, se lo intendo nel primo modo è possibile che abbia una coppia di donne, mentre la secodna interpretazione esclude questo caso....
"Gatto89":
E' vero che può capitare che il giocatore di sinistra abbia due donne, ma la probabilità non è altissima.
Il giocatore alla mia sinistra NON puo' avere una coppia di donne. Nel senso che la formula applicata ci determina la possibilità che io abbia 3 ( e solo 3 [nemmeno 4]) donne. Quindi ne rimane un'altra, che potrebbe o non potrebbe avere il mio compagno.[/quote]
Quelle erano le considerazioni sui casi possibili nel caso il giocatore di destra potesse avere full (l'altra interpretazione del testo, anche se meno probabile)
ma ci siamo arresi ? 
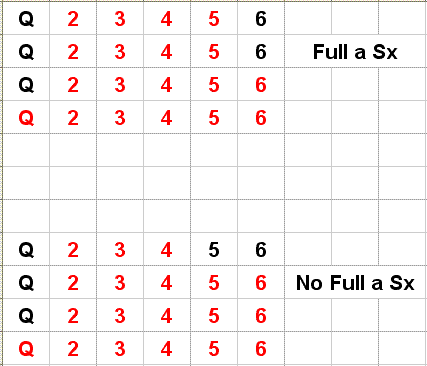
L'immagine in alto mostra la situazione in cui il giocatore a sinistra ha un full, quella in basso non ha il full.
Con 4 Cinque e 2 Sei ho una maggiore probabilità di fare un full( condizione da scartare) rispetto alla seconda ipotesi 3 Cinque e 3 Sei.
Pertanto se si esclude (cosi come il testo sembra escludere), che il giocatore alla mia sinistra abbia un full, la mia % di fare un tris cala leggermente.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo