***Interessante*** Massimo di variabili aleatorie
Mi trovo a dover calcolare la distribuzione M=max(X,Y), dove il vettore $[X Y]$si distribuisce uniformemente sul dominio $|x|+|y|<1$. Se le due variabili aleatorie fossero indipendenti saprei cosa fare, ma in questo caso non lo sono e quindi non capisco come procedere.
Grazie
Grazie
Risposte
carino! mai visto prima. disegna il dominio (un rombo) e vedi $AAz in Z$ quanto vale $mathbb{P}[X<=z,Y<=z]$
tieni presente che tale probabilità è data da $"Area "xx" Densità "$
se non riesci inizia a farlo con variabili uniformi ed indipendenti con il metodo che ti ho descritto...tanto lì la soluzione la conosci....
tieni presente che tale probabilità è data da $"Area "xx" Densità "$
se non riesci inizia a farlo con variabili uniformi ed indipendenti con il metodo che ti ho descritto...tanto lì la soluzione la conosci....
Allora... la densità sarà 1/2 nel rombo e zero all'esterno, e quindi nel caso di indipendenza il massimo sarà $P(max{X, Y}
Non hai capito. Le variabili definite sul rombo non possono essere indipendenti. Valuta quanto vale l'area $(X
Il mio suggerimento di partire con variabili indipendenti uniformi, ad esempio su $(0;1)$, era per verificare che la CDF ti viene proprio $z^2$...non di applicare la formula del libro...
Il mio suggerimento di partire con variabili indipendenti uniformi, ad esempio su $(0;1)$, era per verificare che la CDF ti viene proprio $z^2$...non di applicare la formula del libro...
Nel caso fossero indipendenti e uniformi in $(0,1)$ avrei un quadrato e dovendo essere $X
In pratica dovrei fare l'integrale doppio con $x$ e $y$ che variano, entrambe, da -infinito a $z$, tenendo presente che la funzione densità vale $1/2$ solo all'interno del rombo e zero altrimenti.
E' corretto?
E' corretto?
Nessun integrale. E' macchinoso stare ad integrare con quel dominio e del tutto inutile. Dato che la distribuzione è uniforme la probabilità, come ti ho già detto prima[nota]è evidente che non leggi ciò che scrivo ma continui ad andare per la tua strada; considerato poi che qui ti ho risposto in maniera dettagliata e non hai nemmeno fatto un cenno...che so, grazie per la risposta ecc ecc, penso sinceramente che sia tempo perso stare a dettagliare tutto il ragionamento e quindi ti devi accontentare del risultato a cui sicuramente perverrai anche da solo, leggendo bene le mie istruzioni[/nota], è data semplicemente dall'area di interesse moltiplicata per la densità, costante e pari ad $1/2$
Con semplici considerazioni geometriche trovi quindi che
$F_M(m)={{: ( 0 , ;m<-1/2 ),( (1+2m)^2/4, ;-1/2<=m<0 ),( 1/4+m , ;0<=m<1/2),( 1-(1-m)^2 , ;1/2<=m<1 ),( 1 , ;m>=1 ) :}$
Ecco il grafico (anche se si vede male, non c'è un flesso; la parte da 0 a 0.5 è una retta)
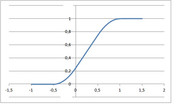

Con semplici considerazioni geometriche trovi quindi che
$F_M(m)={{: ( 0 , ;m<-1/2 ),( (1+2m)^2/4, ;-1/2<=m<0 ),( 1/4+m , ;0<=m<1/2),( 1-(1-m)^2 , ;1/2<=m<1 ),( 1 , ;m>=1 ) :}$
Ecco il grafico (anche se si vede male, non c'è un flesso; la parte da 0 a 0.5 è una retta)


OK grazie mille, ho capito il ragionamento da fare in questi casi!
Tutor AI
Ciao! Sono il tuo Tutor AI, il compagno ideale per uno studio interattivo. Utilizzo il metodo maieutico per affinare il tuo ragionamento e la comprensione. Insieme possiamo:
- Risolvere un problema di matematica
- Riassumere un testo
- Tradurre una frase
- E molto altro ancora...
Il Tutor AI di Skuola.net usa un modello AI di Chat GPT.
Per termini, condizioni e privacy, visita la relativa pagina.
Per termini, condizioni e privacy, visita la relativa pagina.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo