Estrazione senza reimmissione
mi dite come fare questo esercizio? penso sia banale ma non riesco a farlo.
in un secchetto vi sono 5 palline numerate dall'uno al cinque. vengono estratte senza reimmissione due palline. calcolare la probabilità che il numero della prima pallina estratta sia maggiore del numero della seconda pallina estratta
in un secchetto vi sono 5 palline numerate dall'uno al cinque. vengono estratte senza reimmissione due palline. calcolare la probabilità che il numero della prima pallina estratta sia maggiore del numero della seconda pallina estratta
Risposte
L'istinto mi suggerisce 0.5.
Se la prima è 1, la seconda è necessariamente maggiore, così come se la prima è 5, la seconda è necessariamente minore.
La situazione è analogamente simmetrica se la prima pescata è 2 o 4, nel senso che le probabilità sono identiche.
Se la prima pescata è la 3, si ha pari probabilità di pescarne una maggiore o minore nella seconda estrazione.
Penso che sia sufficiente dimostrare la simmetria.
Aspetto comunque conferme.
Se la prima è 1, la seconda è necessariamente maggiore, così come se la prima è 5, la seconda è necessariamente minore.
La situazione è analogamente simmetrica se la prima pescata è 2 o 4, nel senso che le probabilità sono identiche.
Se la prima pescata è la 3, si ha pari probabilità di pescarne una maggiore o minore nella seconda estrazione.
Penso che sia sufficiente dimostrare la simmetria.
Aspetto comunque conferme.
capito... solo che calcoli o modelli non ce ne sono... spero che gli basti il discorso
il modello c'è. sono le 20 coppie ordinate di numeri appartenenti al prodotto cartesiano {1,2,3,4,5}x{1,2,3,4,5} da cui vanno tolte quelle con due elementi uguali.
delle 20 coppie cordinate, 10 hanno il primo elemento maggiore del secondo e 10 il primo elemento minore del secondo. quindi, la probabilità può essere espressa come rapporto 10/20, cioè giustamente 1/2. spero sia chiaro. ciao.
delle 20 coppie cordinate, 10 hanno il primo elemento maggiore del secondo e 10 il primo elemento minore del secondo. quindi, la probabilità può essere espressa come rapporto 10/20, cioè giustamente 1/2. spero sia chiaro. ciao.
Avevo pensato anche io all'eventuale modello.
Basta pensare ad una tabella a doppia entrata, in cui ogni elemento è dato dalla differenza tra numero di riga (primo estratto) e numero di colonna (secondo estratto).
Escludendo la diagonale principale che non rientra nelle soluzioni ammissibili (non c'è reinserimento), tutto ciò che sta al di sopra è positivo (primo estratto maggiore del secondo), tutto ciò che sta al di sotto è negativo (primo estratto minore del secondo).
Basta pensare ad una tabella a doppia entrata, in cui ogni elemento è dato dalla differenza tra numero di riga (primo estratto) e numero di colonna (secondo estratto).
Escludendo la diagonale principale che non rientra nelle soluzioni ammissibili (non c'è reinserimento), tutto ciò che sta al di sopra è positivo (primo estratto maggiore del secondo), tutto ciò che sta al di sotto è negativo (primo estratto minore del secondo).
si si è chiaro
E se si chiede: estratte 3 palle senza reimmissione, qual é la probabilità che i numeri estratti (fra 1 e 5) siano in ordine decrescente?
Forse così il problema diventa un po' più interessante. Più in generale:
In un'urna ci sono N palle numerate da 1 a N e ne estrai, senza reimmissione, K, annotando anche l'ordine con cui escono i K numeri estratti. Qual'é la probabilità che i K numeri siano in ordine crescente?
Forse così il problema diventa un po' più interessante. Più in generale:
In un'urna ci sono N palle numerate da 1 a N e ne estrai, senza reimmissione, K, annotando anche l'ordine con cui escono i K numeri estratti. Qual'é la probabilità che i K numeri siano in ordine crescente?
$1/(k!)$
La simmetria puoi anche rappresentarla graficamente, per una visione piu' chiara, in questo modo:
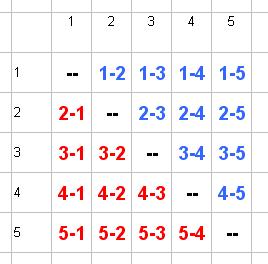

Per UMBY
Non sapevo che fossi così compassionevole e didascalico (o didascalica?) la domenica pomeriggio!
Non sapevo che fossi così compassionevole e didascalico (o didascalica?) la domenica pomeriggio!
[quote=Cheguevilla]$1/(k!)
Sbagliato alla grande!
Sarebbe quella la risposta solo se fosse N=k, cioè se si estraessero tutte le palle dall'urna dalla prima all'ultima.
Ma qui il problema chiedeva di risolvere il caso generale in cui risulta k < N.
C'è qualcuno che sa dare una risposta?
Hint: Bisogna lavorare sulle disposizioni di N elementi a k a k, non sulle permutazioni di k elementi.
Warning: Guai a chi volesse lavorare, in questo contesto, sui prodotti cartesiani à la Ada. Ancor di peggio aspetterebbe chi volesse dedicarsi alle fantasmagoriche illustrazioni pittoriche, à la Umby, di tali prodotti cartesiani.
Sbagliato alla grande!
Sarebbe quella la risposta solo se fosse N=k, cioè se si estraessero tutte le palle dall'urna dalla prima all'ultima.
Ma qui il problema chiedeva di risolvere il caso generale in cui risulta k < N.
C'è qualcuno che sa dare una risposta?
Hint: Bisogna lavorare sulle disposizioni di N elementi a k a k, non sulle permutazioni di k elementi.
Warning: Guai a chi volesse lavorare, in questo contesto, sui prodotti cartesiani à la Ada. Ancor di peggio aspetterebbe chi volesse dedicarsi alle fantasmagoriche illustrazioni pittoriche, à la Umby, di tali prodotti cartesiani.
$(C_(n,k))/(D_(n,k))$
Ma poichè $C_(n,k)=(D_(n,k))/(P_(k))$
Allora $(C_(n,k))/(D_(n,k))=1/(k!)$
Ma poichè $C_(n,k)=(D_(n,k))/(P_(k))$
Allora $(C_(n,k))/(D_(n,k))=1/(k!)$
[quote=Cheguevilla]$(C_(n,k))/(D_(n,k))$
Ma poichè $C_(n,k)=(D_(n,k))/(P_(k))$
Allora $(C_(n,k))/(D_(n,k))=1/(k!)
---------------------------------------------
Giusto! Touché!
Avevo sottovalutato la profondità della tua formula!
Sai, la foto-tessera che ti indentifica sul forum non è che ispiri molta fiducia sulle tue capacità analitiche.
Sono felice di essermi sbagliato.
Ma poichè $C_(n,k)=(D_(n,k))/(P_(k))$
Allora $(C_(n,k))/(D_(n,k))=1/(k!)
---------------------------------------------
Giusto! Touché!
Avevo sottovalutato la profondità della tua formula!
Sai, la foto-tessera che ti indentifica sul forum non è che ispiri molta fiducia sulle tue capacità analitiche.
Sono felice di essermi sbagliato.
Sai, la foto-tessera che ti indentifica sul forum non è che ispiri molta fiducia sulle tue capacità analitiche.Hint: non giudicare mai dall'apparenza. Potrebbe, un giorno, costarti molto caro.
Warning: cerca di mantenere un atteggiamento un po' più rilassato. Sputare sentenze a destra e a manca non aiuta a renderti simpatico, soprattutto quando le sentenze sono completamente fuori portata.
"Cheguevilla":Hint: non giudicare mai dall'apparenza. Potrebbe, un giorno, costarti molto caro.Sai, la foto-tessera che ti indentifica sul forum non è che ispiri molta fiducia sulle tue capacità analitiche.
Warning: cerca di mantenere un atteggiamento un po' più rilassato. Sputare sentenze a destra e a manca non aiuta a renderti simpatico, soprattutto quando le sentenze sono completamente fuori portata.
Grazie, papà, d'ora in poi seguirò scrupolosamente i tuoi preziosi consigli!
Bravo, figliolo, sono qui per questo!
"Enzo":
....Ancor di peggio aspetterebbe chi volesse dedicarsi alle fantasmagoriche illustrazioni pittoriche, à la Umby, di tali prodotti cartesiani.
carina.......
Non capisco: Enzo stava facendo dell'ironia sullo schema a colori di Umby? O che? 


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo