Esercizio Variabile Casuale Bernoulliana e Normale

[devt]

Buonasera,

Ho alcuni punti di un esercizio nella quale non sono riuscito a fare molto onestamente, qualcuno sa come procedere?

$X$ è una variabile casuale bernoulliana di param $p$ quindi $X~B(p)$

$a)$ Esprimere in funzione di $p$ la seguente probabilità: $P(X<=0.5)$

$b)$ Controllare che $Var(X) <= 1/4$

$c)$ Dato $epsi > 0$ numero reale e $n>1$ intero, verificare che $P(|T - p| <= epsi) >= 1 - delta$ con $T=$ media campionaria

Sia $Y$ variabile casuale binomiale di parametri $n=37$ e $p=0.35$
Sia $N$ variabile casuale normale con lo stesso valore atteso e varianza di $Y$

$d)$ Calcolare $P(|Y-E(Y)|<=1.5)$ ed $P(|N-E(N)|<=1.5)$

Per la $a$ non sono sicuro ma ho guardato la funzione di ripartizione e quindi ho risposto $1-p$
Per la $b$ non so onestamente come procedere, l'unica informazione che mi viene in mente è che la $Var$ di una bernoulliana è massima con $p=1/2$ ma oltre a ciò non so altro...
Per la $c$ penso si debba utilizzare la disuguaglianza di Chebyshev con la quale arriverei a dire $... >= sigma^2/epsi^2$ ma non so quanto mi possa aiutare...
Per la $d$ ho fatto il seguente ragionamento:
So che $Y ~ B(n,p)$ e siccome $n$ è ragionevolmente grande posso applicare il teorema del limite centrale quindi
$Y ~ N(np, sqrt(np(1-p)))$ cioè $Y ~ N(12.95, 2.90)$ allora $P(-0.51<= Z <= 0.51)$ cioè $2Phi(0.51)-1 = 0.38$, può tornare? Nel caso della seconda probabilità però mi verrebbe lo stesso procedimento e risultato, cosa sto sbagliando?

Grazie mille, so che sono tanti ma ho preferito inserirli in un solo post piuttosto che spacchettarli in più argomenti.

[Lo_zio_Tom]

"tatoalo":
Per la $a$ non sono sicuro ma ho guardato la funzione di ripartizione e quindi ho risposto $1-p$

giusto

"tatoalo":
Per la $b$ non so onestamente come procedere, l'unica informazione che mi viene in mente è che la $Var$ di una bernoulliana è massima con $p=1/2$ ma oltre a ciò non so altro...

...e mi pare più che sufficiente: $p(1-p)]_(p=0.5)=1/4$

"tatoalo":
Per la $c$ penso si debba utilizzare la disuguaglianza di Chebyshev ... ma non so quanto mi possa aiutare...

Secondo me molto:

$mathbb{P}[|bar(X)-p|=1-delta$

$mathbb{P}[(bar(X)-p)^2=1-(mathbb{E}[bar(X)-p]^2)/epsilon^2$

che è come dire:

$1-(p(1-p))/(n epsilon^2)>=1-delta$

con $delta>(p(1-p))/(n epsilon^2)$ oppure $n>(p(1-p))/(delta epsilon^2)$

"tatoalo":
Per la $d$ ho fatto il seguente ragionamento:
Nel caso della seconda probabilità però mi verrebbe lo stesso procedimento e risultato, cosa sto sbagliando?

Non stai considerando che una variabile è discreta mentre l'altra continua...quindi per la variabile $Y$ avrai che

$mathbb{P}[|Y-mu_Y|<=1.5]=mathbb{P}[11.45<=Y<=14.45]=" essendo definita solo su valori interi "=mathbb{P}[11<=Y<=15]$

ora puoi scegliere come proseguire:

1) per approssimazione e quindi applicare De Moivre Laplace, per la verità anche utilizzando un opportuno fattore di correzione: $Phi(0.8789)-Phi(-0.8445)~~0.6111$

2) calcolare la probabilità richiesta direttamente ed esattamente con la binomiale...è la somma di 5 probabilità, si può fare, ottenendo il valore esatto di $0.6105....$

Per quanto riguarda la variabile normale va bene come hai fatto...anche se non viene $mathbb{P}[|Z|<=0.51]$ ma $mathbb{P}[|Z|<=0.517]~~0.3948$ ....quindi valori sensibilmente diversi fra di loro

"tatoalo":
so che sono tanti ma ho preferito inserirli in un solo post .

e sticazzi.....

[devt]

"tommik":
e sticazzi.....

Grazie mille, sei stato gentilissimo

L'unica cosa che riguardando mi è venuta da gestirla in modo diverso è la $d$ sulla variabile discreta, io la bernoulliana la posso vedere come una normale (T.L.C.) e poi una volta trasformata arrivavo sempre a $2Phi(0.51) - 1$, essendo un'approssimazione penso si perda, come d'aspettarsi, un po' di precisione però non penso sia errato, spero.

[Lo_zio_Tom]

non hai capito. Come hai fatto tu è assolutamente errato.

Per quanto riguarda la variabile normale $X~N(12.95;2.90^2)$ tutte le seguenti probabilità danno lo stesso risultato


$mathbb{P}[11.45<=X<=14.45]=mathbb{P}[11.45
Quindi Standardizzi (come correttamente hai fatto) e calcoli

$mathbb{P}[-0.52<=X<=+0.52]=0.395$

ovvero circa il 40%. Fin qui tutto ok.

Ora passiamo alla binomiale. Qui le cose stanno diversamente...la probabilità $mathbb{P}[11.45<=Y<=14.45]$ va modificata perché la binomiale è discreta e quindi è come dire $mathbb{P}[11<=Y<=15]=mathbb{P}[Y=11]+mathbb{P}[Y=12]+mathbb{P}[Y=13]+mathbb{P}[Y=14]+mathbb{P}[Y=15]=61.05%$

che è molto diverso dal 40% trovato con la gaussiana.

Se, e sottolineo se, vuoi approssimare il calcolo della probabilità binomiale con il TLC, devi sempre partire dal calcolo di $mathbb{P}[11<=Y<=15]$....e considerare che, dato il carattere discreto della distribuzione, devi ampiare l'intervallo di 0.5 punti a sinistra e 0.5 punti a destra ottenendo così

$mathbb{P}[(10.5-12.95)/(2.90)<=Z<=(15.5-12.95)/(2.90)]=Phi(0.8789)-Phi(-0.8445)=61.1%$

che, come puoi notare, è un'approssimazione molto buona del valore esatto $61.05%$

Ecco anche una rappresentazione grafica del problema (ho fatto il grafico parziale della tua binomiale, tralasciando i valori con probabilità $rarr 0$):

(cliccami per ingrandirmi)


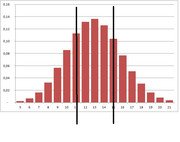
Tu devi calcolare la probabilità delle 5 colonne dell'istogramma. Come vedi la distribuzione non è esasttamente simmetrica. Il problema di "come" la calcoli, ovvero con la binomiale in modo esatto oppure con il TLC in modo approssimato deve ricalcare la realtà. Facendo $Phi(0.52)-Phi(-0.52)=40%$ come vorresti fare tu è completamente sbagliato perché innanzitutto consideri la probabilità solo delle colonne $12,13,14$ dell'istogramma, dimenticando di inserire la 11 e la 15 e poi non consideri il fatto che la distribuzione in oggetto $"Bin"(37;0.35)$ non è simmetrica.

Ci sono numerosi esempi sul forum su come trattare il fattore di correzione per popolazioni discrete....dacci un'occhiata, ad esempio questo

Questo, voleva il tuo prof.....leggi bene ciò che ho scritto e fammi sapere eventuali dubbi.

ciao