Esercizio sul teorema di Bayes
Tommik scusa se ti disturbo ancora...
Ho provato a fare il seguente esercizio per vedere se avevo capito
Un concorso prevede una fase di screening basata su 4 domande a risposta multipla.
I candidati preparati (A), che sono il 20% del totale, danno risposta corretta ad un quesito con
probabilità pA = 3/4, indipendentemente per ogni quesito. Quelli non preparati (B), che sono il
restante 80%, danno invece risposta corretta con probabilità pB = 1/4, sempre indipendentemente
per ogni quesito. La fase di screening si supera dando almeno 3 risposte corrette. Determinare la
probabilità che
1. un candidato preparato superi lo screening;
2. un candidato che supera lo screening non sia preparato;
3. per un candidato lo screening dia la valutazione errata;
4. un candidato sbagli risposta alla seconda domanda se ha sbagliato già la prima.
La 1. mi è sembrato un caso analogo all'esercizio precedente e ho trovato che la probabilità che il candidato a superi il test sia circa 0.85.
La 2. ho provato innanzitutto a calcolare la probabilità che b superi il test, ma essa mi viene stranamente alta circa 0.54 che mi fa sospettare di non averla calcolata correttamente, avendo inoltre utilizzato lo stesso ragionamento che ho applicato per la 1. credo che ho sbagliato anche la prima
Ho provato a fare il seguente esercizio per vedere se avevo capito
Un concorso prevede una fase di screening basata su 4 domande a risposta multipla.
I candidati preparati (A), che sono il 20% del totale, danno risposta corretta ad un quesito con
probabilità pA = 3/4, indipendentemente per ogni quesito. Quelli non preparati (B), che sono il
restante 80%, danno invece risposta corretta con probabilità pB = 1/4, sempre indipendentemente
per ogni quesito. La fase di screening si supera dando almeno 3 risposte corrette. Determinare la
probabilità che
1. un candidato preparato superi lo screening;
2. un candidato che supera lo screening non sia preparato;
3. per un candidato lo screening dia la valutazione errata;
4. un candidato sbagli risposta alla seconda domanda se ha sbagliato già la prima.
La 1. mi è sembrato un caso analogo all'esercizio precedente e ho trovato che la probabilità che il candidato a superi il test sia circa 0.85.
La 2. ho provato innanzitutto a calcolare la probabilità che b superi il test, ma essa mi viene stranamente alta circa 0.54 che mi fa sospettare di non averla calcolata correttamente, avendo inoltre utilizzato lo stesso ragionamento che ho applicato per la 1. credo che ho sbagliato anche la prima
Risposte
"Beps97":
Tommik scusa se ti disturbo ancora...
non vorrei sembrare scortese ma non sono il tuo "personal tutor"....tu poni un quesito alla Community, ogni quesito in un nuovo topic, scrivi per bene TUTTI i conti ed i ragionamenti fatti...se qualcuno ha voglia e tempo ti aiuterà.
Qui non vedo alcun conto o ragionamento da parte tua....ad ogni modo ecco come risolvere il punto 2)...così almeno hai un indizio per tutto il resto
E' una probabiltà condizionata...applica la definzione
$mathbb{P}["non preparato"|"supera lo screening"]=(0.8[((4),(3))0.25^3*0.75+0.25^4])/(0.2[((4),(3))0.75^3*0.25+0.75^4]+0.8[((4),(3))0.25^3*0.75+0.25^4])~~21.58%$
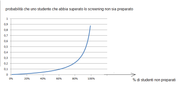
Il risultato finale ti sembra alto? Dipende molto dalla prevalenza dei non preparati sul totale studenti, come si vede bene dal seguente grafico (e che potresti fare anche tu....)
(click per ingrandire)
Grazie per la risposta,
ho corretto la prima risposta così
1. $ mathbb{P}["supera lo screening"|"preparato"]=[((4),(3))0.75^3*0.25+0.75^4]=0.73 $
Per la 3 ho provato a ragionare così
3. L'ho interpretato come $ mathbb{P}["non supera lo screening"|"preparato"]*0.2+ ["supera lo screening"|" non preparato"]*0.8 $
Dove $ mathbb{P}["non supera lo screening"|"preparato"]= 1 - mathbb{P}["supera lo screening"|"preparato"]=0.27 $
mentre $ mathbb{P}[" supera lo screening"|" non preparato"]=[((4),(3))0.25^3*0.75+0.25^4]=0.05$
4. Non ho capito come impostarla
ho corretto la prima risposta così
1. $ mathbb{P}["supera lo screening"|"preparato"]=[((4),(3))0.75^3*0.25+0.75^4]=0.73 $
Per la 3 ho provato a ragionare così
3. L'ho interpretato come $ mathbb{P}["non supera lo screening"|"preparato"]*0.2+ ["supera lo screening"|" non preparato"]*0.8 $
Dove $ mathbb{P}["non supera lo screening"|"preparato"]= 1 - mathbb{P}["supera lo screening"|"preparato"]=0.27 $
mentre $ mathbb{P}[" supera lo screening"|" non preparato"]=[((4),(3))0.25^3*0.75+0.25^4]=0.05$
4. Non ho capito come impostarla
"Beps97":
4. Non ho capito come impostarla
Se qualcuno sbaglia la prima domanda, quali sono le probabilità che sia preparato / non preparato?
Cosa succederà con la seconda domanda?
Ho provato a fare così ma dubito della corretezza del ragionamento ho che:
$ P(B)=0.75 $ probabilità che uno studente non preparato sbagli la prima risposta
$ P(A)=0.25 $ probabilità che uno studente preparato sbagli la prima risposta
gli studenti sono al $ 80% $ B e a $ 20 % $ A
in totale gli studenti che sbagliano la prima domanda sono 65% di questo $ 65% $ il $ 92% $ è uno studente B e il restante $ 8% $ è uno studente A
(Qui credo di aver sbagliato)
il $ 92%$ sbaglia con $P(B)$
il $8%$ sbaglia con $P(A)$
da qui ricavo che circa $70%$ degli studenti che sbagliano la prima domanda sbagliano anche la seconda quindi la percentuale di studenti che sbaglia le prime due domande è di circa il $45%$
$ P(B)=0.75 $ probabilità che uno studente non preparato sbagli la prima risposta
$ P(A)=0.25 $ probabilità che uno studente preparato sbagli la prima risposta
gli studenti sono al $ 80% $ B e a $ 20 % $ A
in totale gli studenti che sbagliano la prima domanda sono 65% di questo $ 65% $ il $ 92% $ è uno studente B e il restante $ 8% $ è uno studente A
(Qui credo di aver sbagliato)
il $ 92%$ sbaglia con $P(B)$
il $8%$ sbaglia con $P(A)$
da qui ricavo che circa $70%$ degli studenti che sbagliano la prima domanda sbagliano anche la seconda quindi la percentuale di studenti che sbaglia le prime due domande è di circa il $45%$
Ma la domanda è "un candidato sbagli risposta alla seconda domanda se ha sbagliato già la prima". Quale delle tue risposte offri per questa domanda?
il 70%
UP, vorrei sapere se i risultati degli altri quesiti sono corretti


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo