Esercizio su densità di probabilità
Si consideri la densità di probabilità
$ f(t) = 3/4 * [1−(t + 1−θ)^2]I(θ−2,θ)(t) $, dove θ è un numero reale incognito.
(a) Si disegni il grafico di f.
(b) Si calcoli il valore atteso µ e la varianza σ2 di una variabile aleatoria con densità f. [µ = θ−1, σ2 = 1/5].
Buonasera, ho difficoltà coi punti di quest'esercizio.
Il primo, non capisco come disegnare quella funzione se theta è incognito.
Il secondo, so che va fatto con l'integrale di x*f(x) nel primo caso e con quello di x^2*f(x) meno quello precedentemente calcolato per la varianza, ma ho difficoltà coi calcoli
$ f(t) = 3/4 * [1−(t + 1−θ)^2]I(θ−2,θ)(t) $, dove θ è un numero reale incognito.
(a) Si disegni il grafico di f.
(b) Si calcoli il valore atteso µ e la varianza σ2 di una variabile aleatoria con densità f. [µ = θ−1, σ2 = 1/5].
Buonasera, ho difficoltà coi punti di quest'esercizio.
Il primo, non capisco come disegnare quella funzione se theta è incognito.
Il secondo, so che va fatto con l'integrale di x*f(x) nel primo caso e con quello di x^2*f(x) meno quello precedentemente calcolato per la varianza, ma ho difficoltà coi calcoli
Risposte
@marcobj99: hai 56 messaggi, mi pare il caso di usare le formule in modo corretto....tutte le formule, non solo la prima.
L'esercizio si risolve tutto in modo immediato e senza noiosi calcoli, però è un esercizio molto ben scritto che ti obbliga a ragionare oppure a perderti in un ammasso informe di calcoli (complimenti al prof )
)
a) riscrivi la densità in questo modo:
$f_T(t)=3/4{-t^2+2(theta-1)t+[1-(theta-1)^2]}mathbb{1}_((theta-2;theta))(t)$
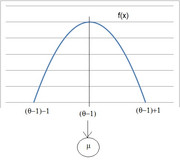
...ora dovrebbe essere evidente quale sia la sua rappresentazione grafica: una parabola[nota]ovvero è una funzione del tipo $y=ax^2+bx+c$[/nota] troncata sul dominio specificato, con i rami rivolti verso il basso e con vertice di ascissa $-b/(2a) = -(2(theta-1))/(-2)=theta-1$....ops abbiamo già calcolato anche la media[nota]nel caso di distribuzione simmetrica ed unimodale infatti media moda e mediana coincidono[/nota] richiesta al punto b)
b)
Prima osservazione
....meno quello precedentemente calcolato "al quadrato"
$V[X]=mathbb{E}[X^2]-mathbb{E}^2[X]$
Seconda osservazione
Per il calcolo della varianza, con un semplice cambio di variabile, ottieni
$V[T]=3/4int_(-1)^(1)[y^2-y^4]dy=3/4[y^3/3-y^5/5]_(-1)^(1)=3/4[2/3-2/5]=1/5$
EDIT:
L'esercizio si risolve tutto in modo immediato e senza noiosi calcoli, però è un esercizio molto ben scritto che ti obbliga a ragionare oppure a perderti in un ammasso informe di calcoli (complimenti al prof
 )
)a) riscrivi la densità in questo modo:
$f_T(t)=3/4{-t^2+2(theta-1)t+[1-(theta-1)^2]}mathbb{1}_((theta-2;theta))(t)$
...ora dovrebbe essere evidente quale sia la sua rappresentazione grafica: una parabola[nota]ovvero è una funzione del tipo $y=ax^2+bx+c$[/nota] troncata sul dominio specificato, con i rami rivolti verso il basso e con vertice di ascissa $-b/(2a) = -(2(theta-1))/(-2)=theta-1$....ops abbiamo già calcolato anche la media[nota]nel caso di distribuzione simmetrica ed unimodale infatti media moda e mediana coincidono[/nota] richiesta al punto b)
b)
Prima osservazione
"marcobj99":
Il secondo, so che va fatto con l'integrale di x*f(x) nel primo caso e con quello di x^2*f(x) meno quello precedentemente calcolato per la varianza, ma ho difficoltà coi calcoli
....meno quello precedentemente calcolato "al quadrato"
$V[X]=mathbb{E}[X^2]-mathbb{E}^2[X]$
Seconda osservazione
Per il calcolo della varianza, con un semplice cambio di variabile, ottieni
$V[T]=3/4int_(-1)^(1)[y^2-y^4]dy=3/4[y^3/3-y^5/5]_(-1)^(1)=3/4[2/3-2/5]=1/5$
EDIT:
Grazie mille, scusa se non ho usato il LaTex.
Comunque, non mi è chiaro come calcoli la varianza, e non capisco quale cambio di variabile utilizzi.
Comunque, non mi è chiaro come calcoli la varianza, e non capisco quale cambio di variabile utilizzi.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo