Esercizietti..per iniziare!
Ho difficoltà nello svolgere questo esercizino..dice:
Due palline sono estratte casualmente da un urna, che ne contiene 10, numerate da 1 a 10. Indicando con X e Y, rispettivamente il risultato della prima e della seconda estrazione, determinare la probabilità che la somma dei numeri delle due palline estratte sia 16 nel caso di estrazioni senza restituzione e nel caso di estrazioni con restituzione..
Una manina per capire i passaggi che devo fare?
Due palline sono estratte casualmente da un urna, che ne contiene 10, numerate da 1 a 10. Indicando con X e Y, rispettivamente il risultato della prima e della seconda estrazione, determinare la probabilità che la somma dei numeri delle due palline estratte sia 16 nel caso di estrazioni senza restituzione e nel caso di estrazioni con restituzione..
Una manina per capire i passaggi che devo fare?
Risposte
pensa ai 100 casi possibili nel caso di reimbussolamento e ai 90 casi possibili in caso che non ci sia reimbussolamento: quanti sono i casi favorevoli?
I casi favorevoli sono dati dal numero di tutte le possibili coppie la cui somma è =16..e fino qua ci siamo e per calcolarne il numero lo vediamo dopo perchè prima vorrei spiegato come arrivi ai 100 e 90 casi possibili 
Ciao.
Io ho ragionato così: dato che dobbiamo considerare la somma delle due palline allora nel caso senza restituzione l'ordine con cui vengono estratte non ha importanza, per cui i casi possibili sono le combinazioni semplici di classe 2 di 10, $C((10),(2))=45$. I casi utili, indipendentemente dall'ordine, sono solo due: (10+6) e (9+7). Le nostre probabilità saranno quindi $2/45=4,44%$ nel primo caso.
Nell'ipotesi del reimbussolamento invece i casi totali sono $10^2=100$ e quelli utili sono cinque (10+6), (6+10), (9+7), (7+9) e (8+8). La probabilità è quindi $5/100=5%$.
Può essere?
Io ho ragionato così: dato che dobbiamo considerare la somma delle due palline allora nel caso senza restituzione l'ordine con cui vengono estratte non ha importanza, per cui i casi possibili sono le combinazioni semplici di classe 2 di 10, $C((10),(2))=45$. I casi utili, indipendentemente dall'ordine, sono solo due: (10+6) e (9+7). Le nostre probabilità saranno quindi $2/45=4,44%$ nel primo caso.
Nell'ipotesi del reimbussolamento invece i casi totali sono $10^2=100$ e quelli utili sono cinque (10+6), (6+10), (9+7), (7+9) e (8+8). La probabilità è quindi $5/100=5%$.
Può essere?
Ma non c'è un modo più veloce con il quale posso trovare il numero di tutte le possibili coppie senza farmi i conticini a mano?
"tabellina": matrice 10 righe 10 colonne. sulle righe i risultati possibili della prima estrazione e sulle colonne quelli della seconda estrazione. con reimbussolamento tutti i casi sono possibili (10 per la prima, 10 per la seconda: in tutto sono 10*10=100 casi).
N.B. i casi si moltiplicano, non si sommano, perché gli esiti sono "coppie ordinate".
gli elementi della diagonale principale (indice di riga = indice di colonna) non vanno condiderati se la seconda estrazione avviene senza reimbussolare la prima pallina estratta: in tal caso due esiti uguali non sono possibili, dunque rimangono 100-10=90 casi.
è chiaro?
ciao.
N.B. i casi si moltiplicano, non si sommano, perché gli esiti sono "coppie ordinate".
gli elementi della diagonale principale (indice di riga = indice di colonna) non vanno condiderati se la seconda estrazione avviene senza reimbussolare la prima pallina estratta: in tal caso due esiti uguali non sono possibili, dunque rimangono 100-10=90 casi.
è chiaro?
ciao.
Si Ada...lo so che dovrò farti una statua in onore alla tua pazienza non appena supererò l'esame di Calcolo ^_^
E per l'ultima domanda che ho posto?
E per l'ultima domanda che ho posto?
io rispondevo ad un'altra domanda... quarda quanti messaggi!
il metodo è abbastanza veloce, ma certo non devi provare tutte le 100 somme per vedere quali vanno considerate!
i numeri possibili sono da 1 a 10. il numero da ottenere è 16. 16/2=8. (8,8) è l'elemento della diagonale principale. posso fare 8+8, 7+9, 6+10, e basta...
quindi distinguendo il risultato della prima estrazione da quello della seconda, ci sono, come già altri hanno scritto, 5 casi favorevoli su 100 (con reimbussolamento) o 4 casi favorevoli su 90 (che è lo stesso da 2 su 45, senza reimbussolamento). ciao.
il metodo è abbastanza veloce, ma certo non devi provare tutte le 100 somme per vedere quali vanno considerate!
i numeri possibili sono da 1 a 10. il numero da ottenere è 16. 16/2=8. (8,8) è l'elemento della diagonale principale. posso fare 8+8, 7+9, 6+10, e basta...
quindi distinguendo il risultato della prima estrazione da quello della seconda, ci sono, come già altri hanno scritto, 5 casi favorevoli su 100 (con reimbussolamento) o 4 casi favorevoli su 90 (che è lo stesso da 2 su 45, senza reimbussolamento). ciao.
ci siamo sovrapposte di nuovo, penso però di aver risposto. fammi sapere.
Quindi tu parti da 8, come elemento della diagonale e vai diminuendo....credo di esserci....e se ho numeri molto piu grandi per i quali devo cercare tutte quelle coppie che mi diano come risultato una determinata somma?
se è una somma solo di due termini, non è che ci siano poi tante possibilità: i possibili esiti sono da 2 a 20, e quelli centrali (10, 11, 12) sono quelli con più casi favorevoli. se ti chiedessero che la somma, anziché 16, faccia ad esempio 30, le possibilità sarebbero nulle.
non so se ho capito quale fosse il tuo dubbio. ciao.
non so se ho capito quale fosse il tuo dubbio. ciao.
Domandina per Stella:
nel caso che hai citato il 16 ha:
il 5% con il reimb. ed il 4,44% senza (quindi una % minore nel secondo caso).
Cosi' come tutti i numeri pari, "perdono peso" senza il reimb., di conseguenza i dispari ne traggono vantaggio.
Perchè ?
nel caso che hai citato il 16 ha:
il 5% con il reimb. ed il 4,44% senza (quindi una % minore nel secondo caso).
Cosi' come tutti i numeri pari, "perdono peso" senza il reimb., di conseguenza i dispari ne traggono vantaggio.
Perchè ?
Bell'osservazione Umby...purtroppo sono una principiante in materia quindi capiti male
piccolo indizio: quanto fa la somma degli elementi della diagonale principale? [non tutti insieme...]
"adaBTTLS":
se è una somma solo di due termini, non è che ci siano poi tante possibilità: i possibili esiti sono da 2 a 20, e quelli centrali (10, 11, 12) sono quelli con più casi favorevoli. se ti chiedessero che la somma, anziché 16, faccia ad esempio 30, le possibilità sarebbero nulle.
non so se ho capito quale fosse il tuo dubbio. ciao.
Mi spiego megli...se mi dicessero ad esempio di effetture...mmmm...3 estrazioni e di calcolare la probabilità che la somma delle palline estratte sia 30 ad esempio...c'è qualche formela particolare per conoscere il numero di tutte le coppie che formano 30? Così anche per un numero sempre crescente di estrazioni di palline, indipendemente dalla loro numerazione (tipo che ho un urna con palline numerate da 1 a 20)
Spero di aver siegato bene la mia curiosità
nel caso che hai detto tu le possibilità sono 8000 ($20^3$), perché non si tratta più di coppie, ma di terne...
sì, ci sono delle formule (ad esempio "numero di composizioni di k in n parti",...), ma non è immediato da lì selezionare le composizioni che fanno al caso nostro per ricondurci alla risoluzione del problema: a me sembra più facile individuare i casi possibili e ricondurci al caso precedente...
comunque il calcolo combinatorio è una scienza relativamente giovane, per cui magari sono stati fatti passi da gigante, ed io nemmeno lo so...
P.S. la formula che ti ho citato di dice che 30 lo puoi scrivere come somma di 3 numeri interi positivi in $((29),(2))=(29*28)/(1*2)=406$ modi, però non ti dice quanti di questi 406 modi sono "accettabili nel tuo caso".
sì, ci sono delle formule (ad esempio "numero di composizioni di k in n parti",...), ma non è immediato da lì selezionare le composizioni che fanno al caso nostro per ricondurci alla risoluzione del problema: a me sembra più facile individuare i casi possibili e ricondurci al caso precedente...
comunque il calcolo combinatorio è una scienza relativamente giovane, per cui magari sono stati fatti passi da gigante, ed io nemmeno lo so...
P.S. la formula che ti ho citato di dice che 30 lo puoi scrivere come somma di 3 numeri interi positivi in $((29),(2))=(29*28)/(1*2)=406$ modi, però non ti dice quanti di questi 406 modi sono "accettabili nel tuo caso".
Ho già chiamato gli Egiziani per far costruire una sfinge con la testa di adaBTTLS...  Grazie del tuo prezioso aiuto!!
Grazie del tuo prezioso aiuto!!
E per quanto riguarda la domanda di Umby?
E per quanto riguarda la domanda di Umby?
nella tabella dei 100 numeri (somme dei numeri che costituiscono le coppie ordinate), 50 sono pari e 50 dispari, mentre sulla diagonale sono tutti pari (sono i doppi dei numeri da 1 a 10), dunque se non li consideri, dei 90 numeri rimanenti 50 sono dispari e 40 pari. un numero pari può essere scritto in un numero dispari di modi come somma di due numeri da 1 a 10, di cui anche quello che corrisponde alla coppia sulla diagonale. diciamo che le probabilità che dovevi trovare sono $(2k+1)/100$ e $(2k)/90$. se invece hai un numero dispari, questo può essere scritto in un numero pari di modi come somma di due numeri da 1 a 10, diciamo 2h, e nessuno corrisponde ad un elemento della diagonale, per cui le due probabilità sono $(2h)/100$ e $(2h)/90$.
in quest'ultimo caso si vede che che la seconda probabilità è sempre maggiore della prima, nel caso precedente ti puoi divertire a vedere che non è sempre il contrario, come si poteva intuire dall'intervento di Umby, ma puoi vedere come il risultato varia con k.
... non lo so ... , sfinge o non sfinge, io non posso entrare nella testa di Umby.
ciao!
in quest'ultimo caso si vede che che la seconda probabilità è sempre maggiore della prima, nel caso precedente ti puoi divertire a vedere che non è sempre il contrario, come si poteva intuire dall'intervento di Umby, ma puoi vedere come il risultato varia con k.
... non lo so ... , sfinge o non sfinge, io non posso entrare nella testa di Umby.
ciao!
Stella, in altre parole il NON reimbussolare il numero estratto determina l'assenza di coppie uguali (1-1, 2-2, 3-3, ... 10-10) che "guarda caso" sono tutte coppie di sommatoria pari! 
Quando sei in difficoltà, puoi farti aiutare da un foglio di calcolo. Impostando qualche semplice formuletta riesci a trovare in tempi brevi la soluzione.
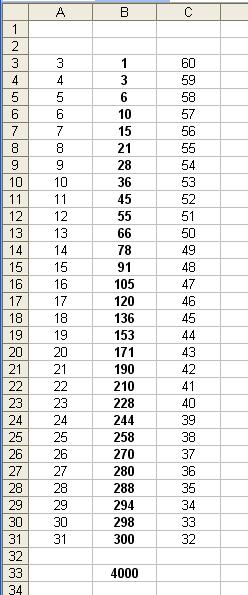
Nell'ultimo caso da te esposto, la tabella mostra la frequenza della sommatoria di 3 estratti con reimbussolamento. Come puoi notare i numeri centrali sono i più frequenti (il 31 ed il 32 con 300 presenze), il 3 ed il 60 ovviamente sono presenti una sola volta (1+1+1 e 20+20+20).
Il numero 30 da te citato, ha una frequenza di 298.
Nell'ultimo caso da te esposto, la tabella mostra la frequenza della sommatoria di 3 estratti con reimbussolamento. Come puoi notare i numeri centrali sono i più frequenti (il 31 ed il 32 con 300 presenze), il 3 ed il 60 ovviamente sono presenti una sola volta (1+1+1 e 20+20+20).
Il numero 30 da te citato, ha una frequenza di 298.

MITICHE!!!  Umby vuoi la sfinge pure tu vero?? Mi conviene fare un mutuo...
Umby vuoi la sfinge pure tu vero?? Mi conviene fare un mutuo...
 Umby vuoi la sfinge pure tu vero?? Mi conviene fare un mutuo...
Umby vuoi la sfinge pure tu vero?? Mi conviene fare un mutuo...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo