Dubbio sulla stima dei parametri

[adriano419]

A partire da un campione $ {X_1, X_2, ..., X_n} $ di ampiezza n estratto dalla seguente
funzione di densità di probabilità:

$ f(x) = (theta-x)/theta^2 { (1 -> 0<=x<=theta),(0-> elsewhere):} $

trovare lo stimatore di M.L. del parametro $ theta $ .

Riscrivo la $ f(x) $ nel modo seguente:

$ f(x)= theta^-2(theta-x) $

con funzione di M.L. $ -> L(theta,x_n)= theta^(-2n)prod _(i=1) ^n(theta-x_i)prod_(i=1)^n 1_{(0,theta)}(x_i) $

ovvero

$ L(theta,x_n)= theta^(-2)(theta-x_1)theta^(-2)(theta-x_2).........theta^(-2)(theta-x_n)=theta^(-2n)(theta-x_i) 1_{(x_(n),+oo)}(theta) $

Che è positiva solo per $ theta>x_n $

Quindi il mio stimatore è $ hatTheta >X_i $ ?

[Lo_zio_Tom]

esercizio interessante, già postato QUI da un altro utente....che però piuttosto che darsi da fare ha preferito chiedere di essere cancellato dal forum.

Prima osservazione: la tua funzione non è una densità di probabilità...prova ad integrare su tutto il dominio e vedrai che non fa 1. La densità corretta è quella che ha scritto l'altro utente nel topic del link. Non cambia nulla, alla fine lo stimatore è quello perché la funzione che hai postato tu è comunque "proporzionale" ad una densità ben posta.

Seconda osservazione: Sarebbe utile, come nell'esempio del link, provare a risolvere l'esercizio per $n=2$ e poi per $n$ generico.
Per $n=2$ ho fatto tutti i conti e nel link ti ho indicato più o meno i passaggi da seguire...non è difficile, una volta stabilito il dominio della verosimiglianza, passi al log, derivi, poni =0 e risolvi (tenendo presente che il dominio è vincolato dal parametro).

Terza osservazione: Per $n>2$, al crescere di $n$, lo stimatore di ML "tende" ad avvicinarsi sempre più a $x_((n))^+$ dove con $x_((n))$ intendo il massimo valore delle osservazioni, ovvero l'ennesima statistica d'ordine.




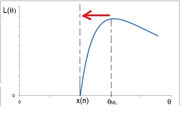
Per arrivare a questa conclusione non è necessario cercare di fare i conti esplicitamente ma bastano alcune osservazioni sulla funzione di verosimiglianza


$L(theta) prop (theta-x_1)/theta^2xx (theta-x_2)/theta^2xx (theta-x_3)/theta^2xx ...xx (theta-x_n)/theta^2xx mathbb(1)_([x_((n));+oo))(theta)$

[adriano419]

Quindi, per prima cosa, correggo la mia densità:

$ f(x) = 2/theta^2(theta-x) {(1-> 0<=x<=theta), (0-> elsewhere):} $

Per $ n=2 $ si ha

$ (2/theta^2)^2prod_ (i=1) ^2(theta-x) = 4/theta^4(alpha-x_1)(alpha-x_2) = 4alpha^-2 - 4alpha^-3x_2 -4alpha^-3x_1 + 4alpha^-4x_1x_2 $

$ (partial)/(partial alpha) = (-8alpha^2 + 12alpha(x_1+x_2) - 16x_1x_2)/alpha^5 $

Dopo un paio di calcoli, ho raggiunto la tua soluzione

$ alpha= 1/4(+-sqrt(9x_1^2 - 14x_1x_2 + 9x_2^2) + 3x_1+3x_2) $

Ovviamente prendo solamente il segno +

$ hatalpha= (sqrt(9x_1^2 - 14x_1x_2 + 9x_2^2) + 3x_1+3x_2)/4 $

Nel caso generico n, in effetti, mi trovo un po' in difficoltà quando applico la log-verosimiglianza. Anche se il docente ha detto che, nel caso di dominio vincolato dal parametro, vuole un ragionamento senza necessità di applicare la log-verosimiglianza.

Quindi partendo dal dominio e dalla funzione di M.L:

$ 0<=x_1<=x_2...<=x_n<=theta $

$ (2/theta^2)^nprod_(i = 1)^(n)(alpha-x_i) = 2^ntheta^(-2n)(alpha-x_1)(alpha-x_2)...(alpha-x_n) $

Non posso considerare $ theta>= x_n $ ma $ theta> x_n $ perché nel caso in cui $ theta= x_n -> hattheta=max{x_i} $ , la funzione di verosimiglianza sarebbe pari a zero.