Distribuzione uniforme - esercizio
Buongiorno, vi propongo questo esercizio
"Il signor Jones è convinto che il tempo di vita di un'automobile (in miglia percorse) abbia distribuzione uniforme sull'intervallo $(0 ; 4*10^4)$.
Il signor Smith ha un'auto che ha già percorso $10$mila miglia.
Se Jones decide di comprarla, che probabilità ha di farle fare almeno altre $20$mila miglia, prima che sia da buttare?"
Io l'ho risolto così:
$10*10^3 + 20*10^3 = 3*10^4$
$P(3*10^4
Non c'è la soluzione sul libro, tuttavia questo esercizio è stato svolto durante le lezioni. Sugli appunti di un ragazzo che ha seguito il corso, la soluzione che è stata appuntata è $0,333$.
Voi pensate che io abbia sbagliato? Se sì, dove?
"Il signor Jones è convinto che il tempo di vita di un'automobile (in miglia percorse) abbia distribuzione uniforme sull'intervallo $(0 ; 4*10^4)$.
Il signor Smith ha un'auto che ha già percorso $10$mila miglia.
Se Jones decide di comprarla, che probabilità ha di farle fare almeno altre $20$mila miglia, prima che sia da buttare?"
Io l'ho risolto così:
$10*10^3 + 20*10^3 = 3*10^4$
$P(3*10^4
Non c'è la soluzione sul libro, tuttavia questo esercizio è stato svolto durante le lezioni. Sugli appunti di un ragazzo che ha seguito il corso, la soluzione che è stata appuntata è $0,333$.
Voi pensate che io abbia sbagliato? Se sì, dove?
Risposte
Ha ragione il tuo amico.
E' una probabilità condizionata. Ti chiede di trovare
$mathbb{P}[X>3|X>1]=(mathbb{P}[X>3])/(mathbb{P}[X>1])=1/3$
Ecco anche il grafico (dati in ascissa espressi in $10^4$ miglia)
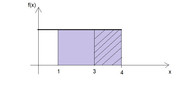
Soluzione: bisognerebbe fare $("area rigata")/("area colorata")$ ma trattandosi di uniforme basta fare $(4-3)/(4-1)=1/3$
Il tuo tentativo di soluzione (un po' maldestro, a dir la verità) non tiene conto delle informazioni in nostro possesso: sappiamo già che 10 mila miglia le ha percorse...e quindi i casi possibili sono più ridotti....sono ridotti a 30 k miglia
E' una probabilità condizionata. Ti chiede di trovare
$mathbb{P}[X>3|X>1]=(mathbb{P}[X>3])/(mathbb{P}[X>1])=1/3$
Ecco anche il grafico (dati in ascissa espressi in $10^4$ miglia)
Soluzione: bisognerebbe fare $("area rigata")/("area colorata")$ ma trattandosi di uniforme basta fare $(4-3)/(4-1)=1/3$
Il tuo tentativo di soluzione (un po' maldestro, a dir la verità) non tiene conto delle informazioni in nostro possesso: sappiamo già che 10 mila miglia le ha percorse...e quindi i casi possibili sono più ridotti....sono ridotti a 30 k miglia
"tommik":
Ha ragione il tuo amico.
E' una probabilità condizionata. Ti chiede di trovare
$mathbb{P}[X>3|X>1]=(mathbb{P}[X>3])/(mathbb{P}[X>1])=1/3$
Ecco anche il grafico (dati in ascissa espressi in $10^4$ miglia)
Soluzione: bisognerebbe fare $("area rigata")/("area colorata")$ ma trattandosi di uniforme basta fare $(4-3)/(4-1)=1/3$
Il tuo tentativo di soluzione (un po' maldestro, a dir la verità) non tiene conto delle informazioni in nostro possesso: sappiamo già che 10 mila miglia le ha percorse...e quindi i casi possibili sono più ridotti....sono ridotti a 30 k miglia
Grazie mille!!
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo