Distribuzione del rapporto
Non riesco a proseguire con i calcoli, quindi temo di aver sbagliato il dominio dell'integrale doppio.
$X_|_YrArrf_(X/Y)=\int_(-\infty)^(+\infty)|x|f_X(x)f_Y(zx)dx$;
$X~ Exp(\lambda_1)rArrf_X(x)=\lambda_1e^(-\lambda_1x)\mathbb(I)_{(x>=0)}$;
$Y~ Exp(\lambda_2)rArrf_Y(y)=\lambda_2e^(-\lambda_2y)\mathbb(I)_{(y>=0)}$.
Pongo $g={ ( u=x/y ),( v=y ):}rArrg'={ ( x=uv ),( y=v ):}$ con $dxdy=|v|dudv$ e osservo che
Se $X$ e $Y$ sono variabili aleatorie esponenziali indipendenti di parametri, rispettivamente, $\lambda_1$ e $\lambda_2$, si determini la distribuzione di $Z=X/Y$.
So che:$X_|_YrArrf_(X/Y)=\int_(-\infty)^(+\infty)|x|f_X(x)f_Y(zx)dx$;
$X~ Exp(\lambda_1)rArrf_X(x)=\lambda_1e^(-\lambda_1x)\mathbb(I)_{(x>=0)}$;
$Y~ Exp(\lambda_2)rArrf_Y(y)=\lambda_2e^(-\lambda_2y)\mathbb(I)_{(y>=0)}$.
Pongo $g={ ( u=x/y ),( v=y ):}rArrg'={ ( x=uv ),( y=v ):}$ con $dxdy=|v|dudv$ e osservo che
$if x>=0->{ ( y=zx=0ifx=0 ),( y=zx=zx ifx>0 ):}rArr0
Qui non sapevo bene come definire l'intervallo quindi ho fatto $0<1
e (credo) siccome l'intervallo è positivo $|v|=v$. Ora avevo pensato di moltiplicare e dividere per $-(\lambda_2+\lambda_1u)$ ma non ottengo la primitiva di $e^(-v(\lambda_2+\lambda_1u)$, quindi non saprei come continuare con i calcoli
Qui non sapevo bene come definire l'intervallo quindi ho fatto $0<1
$f_(X/Y)=\lambda_1lambda_2\int_(1)^(zu)|v|e^(-v(\lambda_2+\lambda_1u))dv$
e (credo) siccome l'intervallo è positivo $|v|=v$. Ora avevo pensato di moltiplicare e dividere per $-(\lambda_2+\lambda_1u)$ ma non ottengo la primitiva di $e^(-v(\lambda_2+\lambda_1u)$, quindi non saprei come continuare con i calcoli
Risposte
più banale di così.....
Tanto per alleggerire la notazione uso $lambda$ e $theta$ come parametri in modo da evitare tutti i pedicelli....
$F_Z(z)=mathbb{P}[X/Y<=z]=mathbb{P}[Y>X/z]=int_0^(+oo)lambda e^(-lambdax)dxint_(x/z)^(+oo) theta e^(- theta y)dy=" due passaggi "=(lambdaz)/(lambdaz+theta)$
$z in (0;+oo)$
Scritta per bene la CDF viene così
e densità (basta derivare la F)
Tanto per alleggerire la notazione uso $lambda$ e $theta$ come parametri in modo da evitare tutti i pedicelli....
$F_Z(z)=mathbb{P}[X/Y<=z]=mathbb{P}[Y>X/z]=int_0^(+oo)lambda e^(-lambdax)dxint_(x/z)^(+oo) theta e^(- theta y)dy=" due passaggi "=(lambdaz)/(lambdaz+theta)$
$z in (0;+oo)$
Scritta per bene la CDF viene così
$F_Z(z)=(lambdaz)/(lambdaz+theta)mathbb{1}_((0;+oo))(z)$
e densità (basta derivare la F)
$f_Z(z)=(lambda theta)/(lambdaz+theta)^2mathbb{1}_((0;+oo))(z)$
Ciao tommik,
anche io avrei qui una domanda. Il problema è che con gli estremi di integrazione spesso mi incarto o comunque o dubbi interpretativi. Adesso aggiungendo un passaggio lecito ma superfluo data l'indipendenza, se non erro, potrei scrivere:
$ F_Z(z)=mathbb{P}[X/Y<=z]=mathbb{P}[Y>X/z]=int_0^(+oo) int_(x/z)^(+oo) lambda e^(-lambdax) theta e^(-thetay)dy dx$
se non fossero indipendenti dovrei risolvere l'integrale doppio con dentro una congiunta non fattorizzabile nel prodotto delle marginali ... ma la domanda è: perchè il primo integrale è calcolato su tutto il dominio ed il concetto di $>$ agisce solo sul secondo?
anche io avrei qui una domanda. Il problema è che con gli estremi di integrazione spesso mi incarto o comunque o dubbi interpretativi. Adesso aggiungendo un passaggio lecito ma superfluo data l'indipendenza, se non erro, potrei scrivere:
$ F_Z(z)=mathbb{P}[X/Y<=z]=mathbb{P}[Y>X/z]=int_0^(+oo) int_(x/z)^(+oo) lambda e^(-lambdax) theta e^(-thetay)dy dx$
se non fossero indipendenti dovrei risolvere l'integrale doppio con dentro una congiunta non fattorizzabile nel prodotto delle marginali ... ma la domanda è: perchè il primo integrale è calcolato su tutto il dominio ed il concetto di $>$ agisce solo sul secondo?
Prova a fare il disegno del dominio $y>x/z$
È la parte di piano del primo quadrante sopra la retta $y=x/z$
puoi integrare così
$int_(0)^(oo)f(x)dxint_(x/z)^(oo)f(y)dy$
oppure così
$int_(0)^(oo)f(y)dy int_(0)^(zy)f(x)dx$
a scelta..in pratica devi fare in modo che le due variabili, variando negli estremi di integrazione che hai identificato, coprano tutta l'area del dominio. È quindi importante fare prima bene il grafico
Ci sono diversi modi di "scrivere" l'integrale doppio; io preferisco scriverli affiancati, risolvi prima l'integrale più a destra...la funzione risultante sarà dipendente dalla variabile integranda in quello di sinistra...risolvi e le due variabili integrate spariscono....e rimane la funzione in $z$
^^^^^^^^^^^^^^^
Vediamo anche un caso più interessante, recentemente postato dall'amico @mobley così magari capisce finalmente che non si può studiare queste cose essendo a totale digiuno di analisi di base.
Supponiamo che il dominio doppio sia il seguente
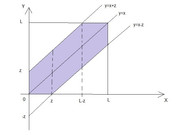
e dobbiamo calcolare la distribuzione del vettore definito sull'esagono viola...per far girare gli estremi di integrazione e far in modo di coprire tutta l'area non c'è verso....occorre spezzettare il dominio in 3 parti e quindi siamo costretti a risolvere il seguente integrale
$F_Z(z)=int_(0)^z dx int_0^(x+z)f(x,y)dy+int_(z)^(L-z) dx int_(x-z)^(x+z)f(x,y)dy+int_(L-z)^(L) dx int_(x-z)^(L)f(x,y)dy$
ho messo la $f(x,y)$ sotto il secondo integrale per fare un caso generale che funziona sempre....tu la metterai dove serve, sotto il primo integrale o il secondo oppure anche fuori se è costante.....ogni caso è a sè.
Come puoi / potete vedere è un dramma da risolvere e ci vuole una settimana....allora ragioniamo.....
Sappiamo che l'integrale della densità su tutto il quadrato $L xx L$ fa uno....ed i due triangoli bianchi sono uguali, per ogni valore di z...diventeranno grossi, per valori di $z rarr0$, avvicinandosi all'esagono oppure piccolissimi per grandi valori di $z rarr L$ ma sempre uguali rimangono....e quindi posso calcolare l'integrale precedente semplicemente integrando uno dei due triangoli ed esprimendo la CDF così:
$F_Z(z)=1-2 int_(0)^(L-z)dx int_(x+z)^(L)f(x,y)dy$
Spero che ora sia un po' più chiaro a tutti come procedere.....nel caso in oggetto (che @mobley conosce bene) il problema si risolve ancora più facilemente senza nemmeno tirare in ballo gli integrali, come ho già spiegato nei dettagli qui in spoiler
@mobley: ti devi dimenticare tutte le formule del libro ed iniziare a ragionare....non puoi usare la formula precotta per calcolare la distribuzione di $Z=Y/X$ quando facendo altrimenti risolvi in due passaggi.
Conosci:
1) le formule già fatte per alcune distribuzioni
2) la convoluzione
3) la definizione di Funzione di ripartizione (usata in questo esempio)
4) il metodo della variabile ausiliaria
Ogni metodo va applicato laddove è più performante.....
Es: se devo calcolare la densità di $Z=X/Y$ di due gaussiane userò la formula precotta perché la definizione di Funzione di Ripartizione diveneterbbe ardua da maneggiare....se lo devo fare con due esponenziali, di integrazione immediata cambio metodo.....
È la parte di piano del primo quadrante sopra la retta $y=x/z$
puoi integrare così
$int_(0)^(oo)f(x)dxint_(x/z)^(oo)f(y)dy$
oppure così
$int_(0)^(oo)f(y)dy int_(0)^(zy)f(x)dx$
a scelta..in pratica devi fare in modo che le due variabili, variando negli estremi di integrazione che hai identificato, coprano tutta l'area del dominio. È quindi importante fare prima bene il grafico
Ci sono diversi modi di "scrivere" l'integrale doppio; io preferisco scriverli affiancati, risolvi prima l'integrale più a destra...la funzione risultante sarà dipendente dalla variabile integranda in quello di sinistra...risolvi e le due variabili integrate spariscono....e rimane la funzione in $z$
^^^^^^^^^^^^^^^
Vediamo anche un caso più interessante, recentemente postato dall'amico @mobley così magari capisce finalmente che non si può studiare queste cose essendo a totale digiuno di analisi di base.
Supponiamo che il dominio doppio sia il seguente

e dobbiamo calcolare la distribuzione del vettore definito sull'esagono viola...per far girare gli estremi di integrazione e far in modo di coprire tutta l'area non c'è verso....occorre spezzettare il dominio in 3 parti e quindi siamo costretti a risolvere il seguente integrale
$F_Z(z)=int_(0)^z dx int_0^(x+z)f(x,y)dy+int_(z)^(L-z) dx int_(x-z)^(x+z)f(x,y)dy+int_(L-z)^(L) dx int_(x-z)^(L)f(x,y)dy$
ho messo la $f(x,y)$ sotto il secondo integrale per fare un caso generale che funziona sempre....tu la metterai dove serve, sotto il primo integrale o il secondo oppure anche fuori se è costante.....ogni caso è a sè.
Come puoi / potete vedere è un dramma da risolvere e ci vuole una settimana....allora ragioniamo.....
Sappiamo che l'integrale della densità su tutto il quadrato $L xx L$ fa uno....ed i due triangoli bianchi sono uguali, per ogni valore di z...diventeranno grossi, per valori di $z rarr0$, avvicinandosi all'esagono oppure piccolissimi per grandi valori di $z rarr L$ ma sempre uguali rimangono....e quindi posso calcolare l'integrale precedente semplicemente integrando uno dei due triangoli ed esprimendo la CDF così:
$F_Z(z)=1-2 int_(0)^(L-z)dx int_(x+z)^(L)f(x,y)dy$
Spero che ora sia un po' più chiaro a tutti come procedere.....nel caso in oggetto (che @mobley conosce bene) il problema si risolve ancora più facilemente senza nemmeno tirare in ballo gli integrali, come ho già spiegato nei dettagli qui in spoiler
@mobley: ti devi dimenticare tutte le formule del libro ed iniziare a ragionare....non puoi usare la formula precotta per calcolare la distribuzione di $Z=Y/X$ quando facendo altrimenti risolvi in due passaggi.
Conosci:
1) le formule già fatte per alcune distribuzioni
2) la convoluzione
3) la definizione di Funzione di ripartizione (usata in questo esempio)
4) il metodo della variabile ausiliaria
Ogni metodo va applicato laddove è più performante.....
Es: se devo calcolare la densità di $Z=X/Y$ di due gaussiane userò la formula precotta perché la definizione di Funzione di Ripartizione diveneterbbe ardua da maneggiare....se lo devo fare con due esponenziali, di integrazione immediata cambio metodo.....
Anzitutto complimenti per il post tommik, fantastico. Ora me lo studio parola per parola.
E' questo il problema. Alcuni esercizi vado spedito e sembra che abbia capito come ragionare, in altri esercizi non cavo un ragno dal buco dimenticando (come ho fatto in questo caso) di poter applicare semplicemente la definizione di ripartizione e derivare. Tu dici ragionare… Non so se ti tratti di occhio, di esperienza… Credo sia questo e io sto facendo esercizi su esercizi.
 E' che spesso e volentieri entro in confusione su cose magari banali perchè non mai "visto" determinati casi o esercizi e quindi ho difficoltà a impostare il ragionamento.[/ot] In ogni caso, come anche l'utente @markowitz ha confermato, la scelta degli estremi di integrazione non è cosa così banale. Rispondendo proprio a lui:
E' che spesso e volentieri entro in confusione su cose magari banali perchè non mai "visto" determinati casi o esercizi e quindi ho difficoltà a impostare il ragionamento.[/ot] In ogni caso, come anche l'utente @markowitz ha confermato, la scelta degli estremi di integrazione non è cosa così banale. Rispondendo proprio a lui:
Come giustamente mi fece capire il geniaccio @tommik la retta $Y=X$ descrive la bisettrice del 1°-3° quadrante, per cui quando ti trovi a dover calcolare una probabilità del tipo
"tommik":
ti devi dimenticare tutte le formule del libro ed iniziare a ragionare....non puoi usare la formula precotta per calcolare la distribuzione di $ Z=Y/X $ quando facendo altrimenti risolvi in due passaggi.
Conosci:
1) le formule già fatte per alcune distribuzioni
2) la convoluzione
3) la definizione di Funzione di ripartizione (usata in questo esempio)
4) il metodo della variabile ausiliaria
Ogni metodo va applicato laddove è più performante.....
Es: se devo calcolare la densità di $ Z=X/Y $ di due gaussiane userò la formula precotta perché la definizione di Funzione di Ripartizione diveneterbbe ardua da maneggiare....se lo devo fare con due esponenziali, di integrazione immediata cambio metodo.....
E' questo il problema. Alcuni esercizi vado spedito e sembra che abbia capito come ragionare, in altri esercizi non cavo un ragno dal buco dimenticando (come ho fatto in questo caso) di poter applicare semplicemente la definizione di ripartizione e derivare. Tu dici ragionare… Non so se ti tratti di occhio, di esperienza… Credo sia questo e io sto facendo esercizi su esercizi.
"tommik":[ot]Beh, il mio 28 ad analisi 1 l'ho strappato quindi proprio a digiuno non ritengo di essere.
Vediamo anche un caso più interessante, recentemente postato dall'amico @mobley così magari capisce finalmente che non si può studiare queste cose essendo a totale digiuno di analisi di base.
"markowitz":
la domanda è: perchè il primo integrale è calcolato su tutto il dominio ed il concetto di $ > $ agisce solo sul secondo?
Come giustamente mi fece capire il geniaccio @tommik la retta $Y=X$ descrive la bisettrice del 1°-3° quadrante, per cui quando ti trovi a dover calcolare una probabilità del tipo
$\mathbb(P)(Y>X),\mathbb(P)(YY),\mathbb(P)(X
con un vettore n-variato continuo, l’ordine di integrazione (prima dy e poi dx) è sempre rispettato. Il motivo attiene al fatto che in $Y=X$ la $x$ è la variabile indipendente (il che vuol dire che il relativo integrale ha estremi di integrazione “fissi”, cioè quelli previsti dall’intervallo di definizione) e la y è la variabile dipendente (e quindi il relativo integrale ha estremi di integrazione “variabili”, cioè individuati in funzione dell’altra variabile). Quindi, se consideri l'esercizio che ho postato io, siccome
per la variabile SEMPRE fissa $X$ si ha $0
con un vettore n-variato continuo, l’ordine di integrazione (prima dy e poi dx) è sempre rispettato. Il motivo attiene al fatto che in $Y=X$ la $x$ è la variabile indipendente (il che vuol dire che il relativo integrale ha estremi di integrazione “fissi”, cioè quelli previsti dall’intervallo di definizione) e la y è la variabile dipendente (e quindi il relativo integrale ha estremi di integrazione “variabili”, cioè individuati in funzione dell’altra variabile). Quindi, se consideri l'esercizio che ho postato io, siccome
$X~Exp(\lambda)->f_X(x)=\lambdae^(-\lambdax) if x\in \mathbb(R)^+$
per la variabile SEMPRE fissa $X$ si ha $0
@tommik grazie per la spiegazione.
Avrei però altre domande.
Effettivamente ho verificato che
$ F_Z(z)=int_0^(+oo) int_(x/z)^(+oo) lambda e^(-lambdax) theta e^(-thetay)dy dx = int_0^(+oo) int_(0)^(zy) lambda e^(-lambday) theta e^(-thetax)dx dy = (lambdaz)/(lambdaz+theta)$
ed i passaggi analitici mi sembrano compresi(*). Tuttavia, nonostante l'esempio, non riesco a "vedere" il grafico che dici. Potresti postarlo?
(*)vorrei solo essere sicuro del fatto che, a patto di ordinare bene le cose, procedere da destra a sinistra come suggerisci sia uguale a procedere dall'interno verso l'esterno.
Poi mi chiedo, se le v.a. di partenza fossero state limitate anche superiormente sarebbe stato corretto fare riferimento ad una forma del tipo:
$ int_(0)^(c_1)f(x)dxint_(x/z)^(c_2)f(y)dy $
oppure così
$ int_(0)^(c_2)f(y)dy int_(0)^(zy)f(x)dx $
dove $c_1$ è l'upper bound di $X$ e $c_2$ quello di $Y$
Avrei però altre domande.
Effettivamente ho verificato che
$ F_Z(z)=int_0^(+oo) int_(x/z)^(+oo) lambda e^(-lambdax) theta e^(-thetay)dy dx = int_0^(+oo) int_(0)^(zy) lambda e^(-lambday) theta e^(-thetax)dx dy = (lambdaz)/(lambdaz+theta)$
ed i passaggi analitici mi sembrano compresi(*). Tuttavia, nonostante l'esempio, non riesco a "vedere" il grafico che dici. Potresti postarlo?
(*)vorrei solo essere sicuro del fatto che, a patto di ordinare bene le cose, procedere da destra a sinistra come suggerisci sia uguale a procedere dall'interno verso l'esterno.
Poi mi chiedo, se le v.a. di partenza fossero state limitate anche superiormente sarebbe stato corretto fare riferimento ad una forma del tipo:
$ int_(0)^(c_1)f(x)dxint_(x/z)^(c_2)f(y)dy $
oppure così
$ int_(0)^(c_2)f(y)dy int_(0)^(zy)f(x)dx $
dove $c_1$ è l'upper bound di $X$ e $c_2$ quello di $Y$
No, in questo caso occorre fare un po' di attenzione.
Vediamo l'esempio in cui il vettore $(X,Y)$ è definito sul rettangolo $[0;2]xx[0;1]$
E' evidente che la variabile $Z=X/Y$ è definita in $(0;+oo)$. Con il solito metodo della Funzione di ripartizione si può calcolare la distribuzione con la stessa definizione dell'esempio precedente, ovvero
$F_Z(z)=mathbb{P}[Y>X/z]$
disegnamo il grafico e vediamo che il dominio assume una forma diversa, a seconda che $z$ sia maggiore o minore di $2$
(click sull'immagine per ingrandirla)
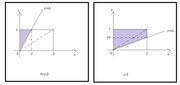
Quindi per trovare la distribuzione di Z integrerai nel seguente modo
$0
$F_Z(z)=int_0^z dx int_(x/z)^1 f(x,y) dy$
oppure, analogamente
$F_Z(z)=int_0^1 dy int_(0)^(zy) f(x,y) dx$
Mentre per la parte $z>2$ integrerai così
$F_Z(z)=int_0^2 dx int_(x/z)^1 f(x,y)dy$
integrare con ordine opposto qui non conviene perché dovresti spezzare l'integrale in due
$F_Z(z)=int_0^(2/z) dy int_(0)^(zy) f(x,y)dx+int_(2/z)^1 dy int_(0)^2 f(x,y)dx$
... Oppure usare un metodo equivalente facendo 1 meno l'integrale sul triangolino bianco....
$F_Z(z)=1-int_0^(2/z)dyint_(zy)^(2)f(x,y)dx$
insomma, più che definire una regola si definisce un "modus operandi"
1) disegnare il grafico del dominio
2) integrare conoscendo bene le basi dell'integrazione doppia....non serve aver fatto un esame di analisi II ma occorre aver BEN CHIARO come integrare un dominio doppio.....ed anche triplo visto che spesso capitano vettori aleatori con 3 variabili...un paio anche postati recentemente
Vediamo l'esempio in cui il vettore $(X,Y)$ è definito sul rettangolo $[0;2]xx[0;1]$
E' evidente che la variabile $Z=X/Y$ è definita in $(0;+oo)$. Con il solito metodo della Funzione di ripartizione si può calcolare la distribuzione con la stessa definizione dell'esempio precedente, ovvero
$F_Z(z)=mathbb{P}[Y>X/z]$
disegnamo il grafico e vediamo che il dominio assume una forma diversa, a seconda che $z$ sia maggiore o minore di $2$
(click sull'immagine per ingrandirla)

Quindi per trovare la distribuzione di Z integrerai nel seguente modo
$0
$F_Z(z)=int_0^z dx int_(x/z)^1 f(x,y) dy$
oppure, analogamente
$F_Z(z)=int_0^1 dy int_(0)^(zy) f(x,y) dx$
Mentre per la parte $z>2$ integrerai così
$F_Z(z)=int_0^2 dx int_(x/z)^1 f(x,y)dy$
integrare con ordine opposto qui non conviene perché dovresti spezzare l'integrale in due
$F_Z(z)=int_0^(2/z) dy int_(0)^(zy) f(x,y)dx+int_(2/z)^1 dy int_(0)^2 f(x,y)dx$
... Oppure usare un metodo equivalente facendo 1 meno l'integrale sul triangolino bianco....
$F_Z(z)=1-int_0^(2/z)dyint_(zy)^(2)f(x,y)dx$
insomma, più che definire una regola si definisce un "modus operandi"
1) disegnare il grafico del dominio
2) integrare conoscendo bene le basi dell'integrazione doppia....non serve aver fatto un esame di analisi II ma occorre aver BEN CHIARO come integrare un dominio doppio.....ed anche triplo visto che spesso capitano vettori aleatori con 3 variabili...un paio anche postati recentemente
Ciao tommik,
proprio a proposito di quanto dicevi mi chiedevo come trattare il seguente caso che mi sembra appropriato aggiungere qui, in caso contrario spostiamo.
Passiamo a 3 variabili esponenziali indipendenti di parametri $lambda_1$, $lambda_2$, $lambda_3$. Definisco $Y=X_1*X_2*X_3$ e devo trovare la sua distribuzione.
Direi
$P(Y<=y)=P(X_1*X_2*X_3<=y)=P(X_1<=y/(X_2*X_3))$ quindi
$ F_Y(y)=int_0^(+oo) int_(0)^(+oo) int_(0)^(y/(x_2*x_3)) lambda_1 lambda_2 lambda_3 e^(-lambda_1 x_1 -lambda_2 x_2 -lambda_3 x_3) dx_1 dx_2 dx_3 = int_0^(+oo) lambda_3 e^(-lambda_3 x_3) dx_3 int_0^(+oo) lambda_2 e^(-lambda_2 x_2) dx_2 int_(0)^(y/(x_2*x_3)) lambda_1 e^(-lambda_1 x_1) dx_1$
è impostato correttamente?
La rappresentazione geometrica è ancora possibile?
proprio a proposito di quanto dicevi mi chiedevo come trattare il seguente caso che mi sembra appropriato aggiungere qui, in caso contrario spostiamo.
Passiamo a 3 variabili esponenziali indipendenti di parametri $lambda_1$, $lambda_2$, $lambda_3$. Definisco $Y=X_1*X_2*X_3$ e devo trovare la sua distribuzione.
Direi
$P(Y<=y)=P(X_1*X_2*X_3<=y)=P(X_1<=y/(X_2*X_3))$ quindi
$ F_Y(y)=int_0^(+oo) int_(0)^(+oo) int_(0)^(y/(x_2*x_3)) lambda_1 lambda_2 lambda_3 e^(-lambda_1 x_1 -lambda_2 x_2 -lambda_3 x_3) dx_1 dx_2 dx_3 = int_0^(+oo) lambda_3 e^(-lambda_3 x_3) dx_3 int_0^(+oo) lambda_2 e^(-lambda_2 x_2) dx_2 int_(0)^(y/(x_2*x_3)) lambda_1 e^(-lambda_1 x_1) dx_1$
è impostato correttamente?
La rappresentazione geometrica è ancora possibile?
Tutor AI
Ciao! Sono il tuo Tutor AI, il compagno ideale per uno studio interattivo. Utilizzo il metodo maieutico per affinare il tuo ragionamento e la comprensione. Insieme possiamo:
- Risolvere un problema di matematica
- Riassumere un testo
- Tradurre una frase
- E molto altro ancora...
Il Tutor AI di Skuola.net usa un modello AI di Chat GPT.
Per termini, condizioni e privacy, visita la relativa pagina.
Per termini, condizioni e privacy, visita la relativa pagina.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo