Deviazione standard e varianza nelle v.a. gaussiane
Buongiorno a tutti, ho un dubbio in merito alle v.a. gaussiane standard e non standard. Studiando ho notato che su alcuni appunti trovo scritto $sigma$ mentre su altri $sigma^2$ o meglio:
v.a. gaussiana standard: $Z ~ N(0; 1) $ con $mu = 0 $ e $sigma=1$
v.a. gaussiana non standard: $X_0 ~ N(mu ; sigma^2)$
La mia domanda è: quale delle due scritture è corretta? Si utilizza la deviazione standard o la varianza per descrivere le v.a. gaussiane sia standard che non standard? Fermo restando che la deviazione standrad è la radice quadrata della varianza però è per chiarire le idee e per fare meno errori possibili.
Grazie a tutti in anticipo.
v.a. gaussiana standard: $Z ~ N(0; 1) $ con $mu = 0 $ e $sigma=1$
v.a. gaussiana non standard: $X_0 ~ N(mu ; sigma^2)$
La mia domanda è: quale delle due scritture è corretta? Si utilizza la deviazione standard o la varianza per descrivere le v.a. gaussiane sia standard che non standard? Fermo restando che la deviazione standrad è la radice quadrata della varianza però è per chiarire le idee e per fare meno errori possibili.
Grazie a tutti in anticipo.
Risposte
la notazione corretta (cioè la notazione che si trova sul 99.99% dei libri di Statistica) è questa
$X~N(mu;sigma^2)$
E' possibile trovare qualche testo che tratti di problemi con la gaussiana (ma di sicuro non è un libro di Statistica) dove viene esplicitamente indicato
$N(mu;sigma)$
anche se dovessi trovare $N(theta;theta)$ significa media e varianza pari a $theta$
Nel caso di gaussiana standard, $N(0;1)$ significa Gaussiana di media zero e VARIANZA 1 (che in tale caso coincide anche con deviazione std 1)
$X~N(mu;sigma^2)$
E' possibile trovare qualche testo che tratti di problemi con la gaussiana (ma di sicuro non è un libro di Statistica) dove viene esplicitamente indicato
$N(mu;sigma)$
anche se dovessi trovare $N(theta;theta)$ significa media e varianza pari a $theta$
Nel caso di gaussiana standard, $N(0;1)$ significa Gaussiana di media zero e VARIANZA 1 (che in tale caso coincide anche con deviazione std 1)
"tommik":
...
grazie per la celere risposta.
Quindi mi confermi che è corretto parlare di varianza piuttosto che di deviazione standard anche nel caso di v.a. gaussiane standrad? Perchè il mio problema è che quell' $1$ che io leggo, in una scrittura può valere $1$ e in un'altra $sqrt(1)$ che non è proprio la stessa cosa
"Marco Beta2":
in una scrittura può valere $1$ e in un'altra $sqrt(1)$ che non è proprio la stessa cosa
è la stessa cosa....la varianza è sempre positiva perché è una misura di distanza, quindi la sua radice è sempre 1
sarebbe interessante capire l'interpretazione geometrica della varianza (o della deviazione std)....se poi ho tempo provo a farti un esempio esplicativo
"tommik":
...
Ottimo sarebbe veramente interessante
graficamente so che piu la dev. standard tende a zero, più la campana della funzione è accentuata... però mi sfugge del perchè sugli appunti (e quindi a lezione) prima si usi la dev. standard e poi la varianza e in maniera molto velata...
dunque consideriamo di avere il seguente campione casuale $(X;Y)$
La deviazione standard del campione (corretta) viene così
$S=sqrt(1/(n-1)[(x-m)^2+(y-m)^2])$
Supponiamo ora che la realizzazione campionaria sia la seguente
$(X=3;Y=1)$
e vediamo cosa succede graficamente
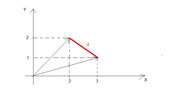
la deviazione standard corretta è, via teorema di pitagora, il segmento rosso $d$, ovvero la distanza fra il vettore $(X=x;Y=y)$ ed il vettore delle medie $(m;m)$
E' quindi evidente che, radice quadrata o meno, la misura risultante è sempre una valida misura di distanza....e nulla cambierebbe se al posto di $(n-1)$ ci mettiamo $n$...sempre di misura di distanza si tratta
In conclusione: parlare di varianza o di deviazione standard in termini di significato non cambia nulla. Cambierà la manifestazione numerica, dovrai stare attento a fare i conti ma concettualmente sono due misure intercambiabili.
La deviazione standard del campione (corretta) viene così
$S=sqrt(1/(n-1)[(x-m)^2+(y-m)^2])$
Supponiamo ora che la realizzazione campionaria sia la seguente
$(X=3;Y=1)$
e vediamo cosa succede graficamente
la deviazione standard corretta è, via teorema di pitagora, il segmento rosso $d$, ovvero la distanza fra il vettore $(X=x;Y=y)$ ed il vettore delle medie $(m;m)$
E' quindi evidente che, radice quadrata o meno, la misura risultante è sempre una valida misura di distanza....e nulla cambierebbe se al posto di $(n-1)$ ci mettiamo $n$...sempre di misura di distanza si tratta
In conclusione: parlare di varianza o di deviazione standard in termini di significato non cambia nulla. Cambierà la manifestazione numerica, dovrai stare attento a fare i conti ma concettualmente sono due misure intercambiabili.
"tommik":
...
Grazie mille tommik, spiegazioni al top come sempre
chiaro e conciso, ora mi è tutto più chiaro Un ultimo dubbio e poi ti libero, nel caso di v.a. gaussiana non standard, nel caso dovessi avere una richiesta di calcolo della CDF o della PDF, dove in entrambe figura $sigma$, quella sarà data dalla radice della varianza data giusto?
sì
Del resto la tua densità rimane sempre questa
$f(x|ul(theta))=1/(sigmasqrt(2pi))e^(-1/(2sigma^2)(x-mu)^2)$
dove $ul(theta)$ è il vettore dei parametri. Normalmente si intende $ul(theta)=(mu;sigma^2)$ ma nessuno vieta di pensare $ul(theta)=(mu;sigma)$
Immagino che la cosa possa creare un po' di confusione ma è così.....
Ovviamente bisogna essere un po "smart" in queste cose....anche questa è una gaussiana...
Del resto la tua densità rimane sempre questa
$f(x|ul(theta))=1/(sigmasqrt(2pi))e^(-1/(2sigma^2)(x-mu)^2)$
dove $ul(theta)$ è il vettore dei parametri. Normalmente si intende $ul(theta)=(mu;sigma^2)$ ma nessuno vieta di pensare $ul(theta)=(mu;sigma)$
Immagino che la cosa possa creare un po' di confusione ma è così.....
Ovviamente bisogna essere un po "smart" in queste cose....anche questa è una gaussiana...
"tommik":
...
Grazie mille è tutto chiarissimo
Hai ragione bisogna essere smart su queste cose e spero che tutto dipende dal farci l'occhio
Grazie ancora e al prossimo dubbio
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo